データを扱う上で抑えておくべき確率の基礎のキ

この記事はNuco アドベントカレンダーの21日目の記事です。

はじめに

株式会社Nucoで見習いエンジニアをしている@noshishiです。
今回は、統計や機械学習に使われる確率的な考え方の基礎を自分なりにまとめてみたいと思います。
クリスマスに向けた楽しい確率の物語をお伝えできれば幸いです。

データと確率

クリスマスが近づくと、いろんな期待が膨らみますよね。
可愛い（カッコいい）あの人とデートしたいなとか。この年になってもサンタさんこないかなとか。このクリスマスの運気に乗ってこの記事伸びないかなとか（祈り）。

この時、気にするのがどれくらいその可能性があるかということではないでしょうか？
あるいは、その可能性を見積もりたいなというモチベーションがあると思います。

そんな時どうすれば良いでしょうか？
データと確率を考えながら、見ていきましょう。

データ

「データ」は、観測された事象のことです。
我々は、日々生活する中で、いろんなデータを生み出しています。
一方で、データとしてまだ観測されていないこともたくさんあります。

そのため、誰がデータを観察しているかが一つのポイントです。
たとえば、Qiitaコーヒーショップがクリスマスに向けて、新しいコーヒーを販売したとしましょう。

Aさんにとってのデータは、自分の購入歴のみです。Bさんは購入歴はデータではないことになります。
Qiitaコーヒショップにとってのデータは、Aさん、Bさんの購入歴です。まだ買っていない人はもちろんデータではないことになります。

確率

「確率」は、ある事象が起こる可能性を考えるツールです。

上の図であれば、Qiitaコーヒーショップが、

• AさんBさんはどんな確率でQiitaコーヒーを買ってくれるのか
• まだ買ってない人がどれくらいの確率で買ってくれるだろうか

と考えることができます。

ただし、現実世界で観測されるデータから真の確率を求めることができない場合がほとんどです。
（一方で、ミクロの世界では理論計算により真の確率を求めることできるそうです。）

この記事での確率は、厳密な定義はしません。
確率が主観的・客観的なのか〜、数学的には〜とか重要な要素ですが、あくまでも、何かの事象が起こる可能性を表した度合いだとして話を進めていきます。

データを扱う上での確率

我々は、いろんな意思決定に確率を使っていたり、無意識に考えてたりします。
降水確率が80%以上であれば傘を持っていこうとか、ガチャのスーパーレアの当選確率が3%以上なら引こうとか。もっと主観的な確率で、去年もクリスマス晴れてたし今年も晴れるだろうと考えたり。
もちろん、考えないこともたくさんあると思います。

でも、重要な意思決定をする時は、できれば事前に確率を知りたいと思うこともあるのではないでしょうか？
そういう時は、自分の手元にあるデータを元に何か法則性（確率）がないかと考えます。

ビジネス上での確率というのは、それぞれの選択肢の可能性を見積もる、判断を下すことが最終目的です。
コーヒショップの例であれば、どんな属性の場合、コーヒーを買うかという法則性を導き出すというのが、確率を扱うということです。

例えば、「エンジニアという職業」で「Qiitaの記事を書いている人」は、Qiitaコーヒーを90%で買ったデータがあれば、同じ条件の人であれば同じような確率で買ってくれるのではないかと考え、エンジニアへのアプローチを増やすという決断ができることになります。

データを分析する上で重要な統計や機械学習には、確率的な思考や理論が大きく関わっています。

統計と機械学習

統計では、手元にあるデータが説明できるようなモデルを考え、その結果を検証し、結論を出すことを目的としています。機械学習は、手元にあるデータをうまく使って、未知のデータに対する予測精度を高くすることを目標にしています。
私の言葉で書いてみましたが、実際のところ統計は、結論の後に、未知のデータを予想することもできるし、機械学習は、学習結果から要因を探ることもできます。

統計学にせよ、機械学習にせよ、根底にあるのはひとまず「目の前にあるデータをモデリングすること」「そのために『ばらつき』をうまく扱うこと」　
尾崎 隆(https://tjo.hatenablog.com/entry/2015/09/17/190000)

という言葉が、私の中では一番ピンときています。

著者も初学者ゆえ、両者の厳密な区別は曖昧なので、ぜひみなさん自身で考えてみてください。
※結局、統計学と機械学習は何が違うのか？を読むとイメージが湧いてきます。

統計も機械学習も、いろんな分野の理論を取り入れて成長している分野です。
機械学習(特に深層学習)であれば、人間の解釈を超えるモデルもあったりします。

確率を学ぶ

データと確率を結びつける出発点は、データは何かしらの確率によって起こっているのではないかを考えることです。
いろんな確率を考える道具が用意されているので、その道具を一つ一つ見ていきましょう。

さて、我々が囚われている架空の都市であるQiita町の12月25日にロマンチックな日となるか（雪が降る可能性）を考えましょう。

2012年から2021年までの12月25日における降雪量のデータがわかっているとしましょう。

年度	2012	2013	2014	2015	2016	2017	2018	2019	2020	2021
降雪の有無	有	有	有	無	有	無	無	有	有	無
降雪量(cm)	10	20	40	0	20	0	0	30	10	0
寒波の有無	有	無	有	無	有	無	有	無	有	無

ちなみに確率は、以下のようにPで表すことが多いです。

P(想定する事象) (= 想定する事象が起こった時の確率)

確率変数

今回は、雪が降るか降らないかまだわからないので、その二値は変数と呼ばれます。
そして、何かしら確率的に決まる変数を、確率変数と言います。
一方で、実際に観測された値を実現値と呼ばれます。
つまり、2012年を例に出すと、降雪の有無という確率変数の実現値が「有」だったということになります。

一般的に確率変数はアルファベットの大文字、実現値は小文字で表現されます。

X...確率変数,x...実現値

確率変数には、今回のような降るか降らないかという離散なものと、降雪量といった連続的なものに分けることができます。

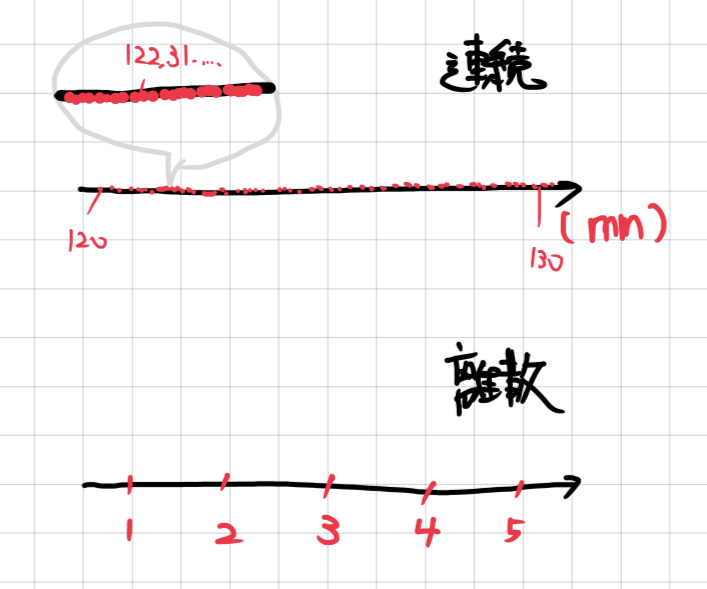
もう少し詳しく分けると、

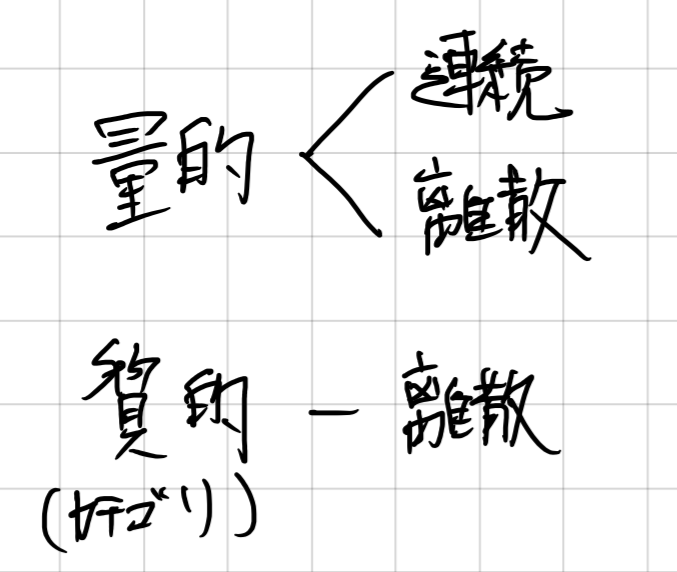
ここからは抽象的に事象を扱うため、確率変数に数値を当てはめましょう。
降雪データをXという確率変数だと考え、降雪が無い場合を０に、降雪がある場合を１としましょう。
※基本的に質的なデータであれば、一方を0, もう一方に1を当てはめることが多いです。

データを確率変数と考えることで、データに確率を導入できる。

確率分布

Qiita町の場合、これまでの雪が降る程度からわかるのではと考えたとしましょう。
データからは10年中に6年降ったので、60%の確率で雪が降りそうだと言えそうです。

つまり、以下のように表すことができます。

P(X=1) = 3/5

確率変数ごとの確率をまとめて表したものを確率分布と呼びます。
さっきのデータの場合は、以下のような分布になります。

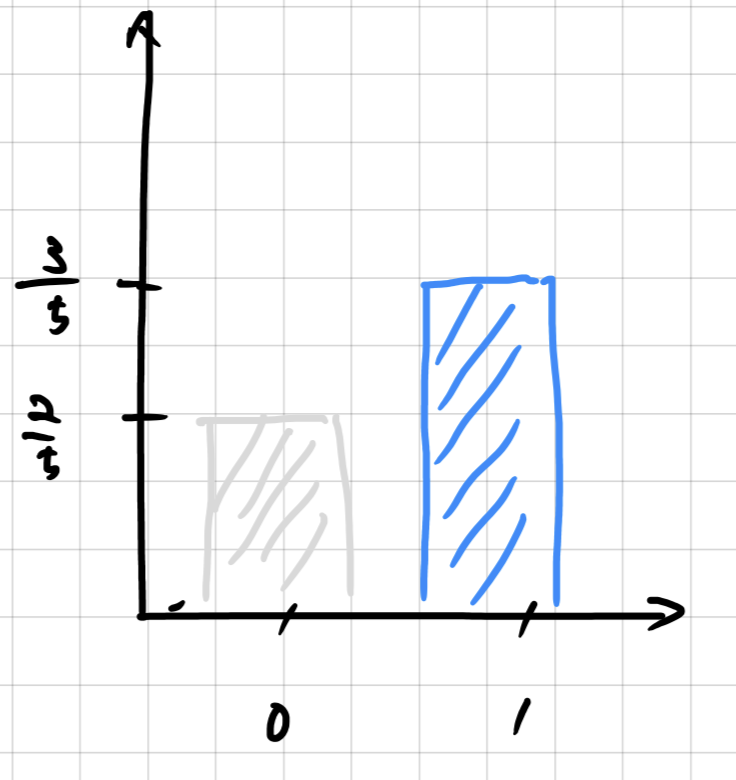
横軸に確率変数を、縦軸を確率とすることで視覚化することが一般的です。
（ちょっと2値なので、なんとも分布感がないのですが、、、後々わかりやすい確率分布を描きます。）

離散確率変数と確率を繋ぐ関数（対応付けしたもの）を、確率（質量）関数と呼ばれています。
今回であれば、以下のような式で表せます。

P(X=1) = 3/5,P(X=0) = 2/5

連続確率変数の場合、確率密度関数と呼ばれるものが、その役割を持ちます。
連続の値の場合、一つの値に対しての確率は取り出せないので、範囲（密度）で確率を算出することになるため、確率関数が違うものになっています。

確率分布を考えば、確率変数の規則性が明らかになる。
確率関数が分かれば、すぐに対応する確率が取り出せます。
ちなみに、確率の合計は１となる性質は確率分布から簡単に求めることができます。
「離散」であればΣ（合計）で、「連続」なら∫（積分）で求めることができます。

確率分布の仮定

統計や機械学習の世界では、この確率分布を代表的な確率分布で想定しておくということがよくあります。
例えば、確率変数が二値である場合、確率分布がベルヌーイ分布に従うと呼ばれたりします。

代表的な確率分布と特徴について簡単にみておきましょう。

ベルヌーイ分布
１回の実験を行った時に成功する確率がpであるような場合の離散確率分布です。
確率質量関数は以下のように表せます。

P(X=k) = p^{k}(1-p)^{1-k} \qquad　k=(0,1)

特徴は、kが起こる確率が確率pによって決まるということです。
さっきの例だと、この確率pがもとまったので、ベルヌーイ分布を求めることができることになります。

二項分布
ベルヌーイ分布は一回の確率に着目していますが、より試行回数を増やし、実験の中で何回事象が起こり得るかを表す離散確率分布です。ベルヌーイ分布を拡張させたものとも言えるでしょう。

確率質量関数は、以下のように表せます。

P(X=k) = nCk*p^{k}(1-p)^{n-k} \qquad　k=(0,1...n)

特徴は、n（試行回数）と一回ごとの確率pが分かれば分布がわかるということです。
ちなみに先ほどの例で、確率p=3/5が求まったとして、10年のうち何年、12月25日に雪が降るかで確率分布を算出してみると以下のようになります。

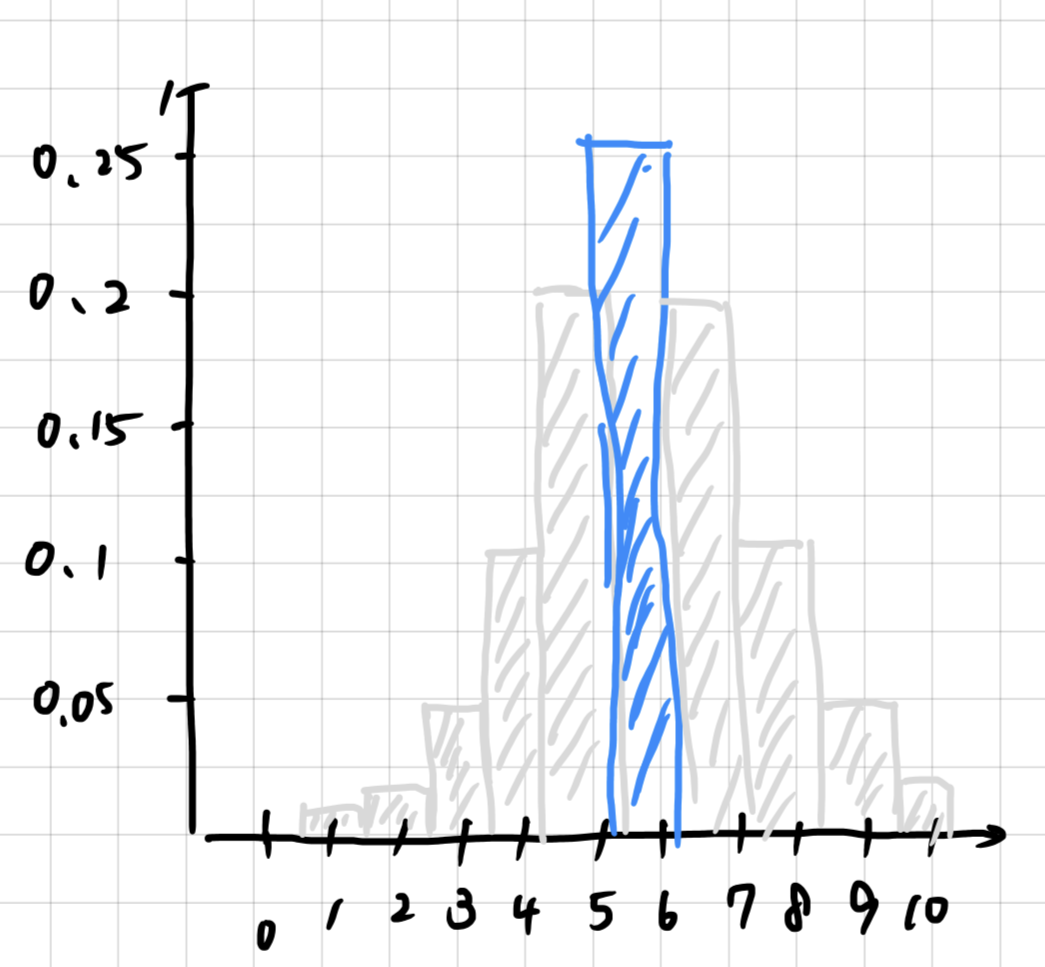
10年のうち6年降る時が、一番確率が高くなることがわかります。

正規（ガウス）分布
分布が特定の位置（平均）で最大となり左右均等に裾が広がる連続確率分布です。
確率密度関数は、以下のように表せます。

f(x)=\dfrac{1}{\sqrt{2\pi\sigma}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})

特徴は、平均μと標準偏差σが分かれば分布がわかるということです。
連続確率変数に対する分布ゆえ、ある点における確率は求めれませんが、平均μからプラスマイナス標準偏差σ分の確率は約68.2パーセントだと決まっています。

P(-\sigma < X < \sigma) = \int_{-\sigma}^{\sigma}f(x)dx　≒　68.2％

一般的に確率変数の確率分布が自明でなければ、正規分布を想定するというのが多いです。というのも中心極限定理と呼ばれる定理によりデータ数が多くなればなるほど、データの平均値が正規分布に従うという法則があるためです。

なぜ、確率変数が従う確率分布を事前に想定しておくかというと、代表的な確率分布は上で記載したようにある値が分かれば数式で表現したり、分布を特定することが容易であるためです。
例えば、ベルヌーイ分布であれば「p」、二項分布では「n, p」、正規分布であれば「μ, σ」のように、分布を特徴づける変数をパラメータといいます。

もちろん、分布を想定せずに、推し量るという方法も存在します。
この場合、分布にかなりの自由が効くものの、非常に計算が困難であることが知られています。

ここでは、ほんの３つだけ紹介しましたが、確率分布の世界はかなり広いです。
統計の検定で使用されるカイの２乗分布やt分布、事前共役で使用されるベータ分布やガンマ分布などなど。
確率分布の曼荼羅図　Univariate Distribution Relationships
（実際どうやって利用されているのかまだまだ未知の世界ですが、、、）

代表的な確率分布は、特徴的な値（パラメータ）によって形が決まっている。
その特徴を利用して、パラメータから分布の形を求めたり、確率を求める。

同時確率と周辺確率

降雪の有無は、寒波の有無も関係していそうな気がします。
つまり、新しい確率変数Yを導入してみましょう（寒波が有る場合は１、無い場合は０）。

複数の確率変数を一緒に考える確率を同時確率と呼ばれます。
同時確率は表に表すとこんな感じになります。

	P(X=1)	P(X=0)
P(Y=1)	2/5	1/10
P(Y=0)	1/5	3/10

つまり、降雪があって、寒波であった確率は2/5となります。

P(X=1, Y=1) = \frac{2}{5}

一方で、片方の確率変数を無視したときの確率(例、雪降るかにかかわらず寒波になる確率)を周辺確率と呼ばれます。

	X=1	X=0
Y=1	2/5	1/10	1/2

つまり寒波である周辺確率は、上の図から1/2であることがわかります。

P(Y=1) = \frac{1}{2}

こうした操作をを周辺化すると呼ばれます。

同時確率は、複数の確率変数があったときに確率を考えることができる。
周辺確率は、複数の確率変数があったときに一つの確率変数に着目して確率を考えることができる。
両者は、複数の確率変数を分解し理解できるツールである。

条件付き確率

降雪の有無は、寒波の有無に左右されているような印象を受けます。
こういった確率変数同士が影響しそうな場合を確率的に記述するのが条件付き確率です。

今回であれば、寒波の有無が降雪の有無に関係してそうなので、その確率を知るというのが条件付き確率になります。
数式は以下のように記述されます。

P(X=1|Y=1) = \frac{P(X=1, Y=1)}{P(Y=1)}

寒波であった場合に雪が降る確率は、4/5であることになります。
つまり、寒波であった場合は、普段の降雪率より高くなりそうだということが考えられます。

条件付き確率は、複数の確率変数同士の関係性に確率を導入できる。
ただし、因果を特定しているわけではないことに注意すること。

ベイズの定理

今までは、実現値を一つに対して条件付き確率を求めましたが、一般的にかくと以下のようになります。

P(X|Y) = \frac{P(X, Y)}{P(Y)}

上記の等式を元に確率変数Xと確率変数Yを入れ替えても成立します。

P(Y|X) = \frac{P(X, Y)}{P(X)}

上記の２つの等式には、どちらもP(X, Y)（同時確率）が含まれているので、式変形を行うと、

P(Y|X) = \frac{P(X|Y) * P(Y)}{P(X)}

と式変形することができます。
これをベイズの定理と呼ばれています。

この式からわかることは、「寒波があった場合の降雪がある確率P(X|Y)」を使って、「降雪があった場合に寒波である確率P(Y|X)」を求めることができるということです。

また、別の見方をすると右辺の分子にあるP(Y)は原因であると考えていたので、事前確率と呼び、左辺の条件付き確率P(Y|X)は事後確率と呼ばれます。
降雪が観測されたときに（事後に）、原因である寒波が発生していた確率を考えていることになります。

ベイズの定理を使った確率の変動をベイズ更新と呼ばれています。
つまり、今回の場合であれば、寒波は事前には1/2の確率だと考えていたが、降雪有の確率を考慮することで、寒波である確率が2/3に更新されたと考えることができます。

推定

先ほどまで行っていた予測を統計では、推定と呼ばれています。
具体的には、2値を取る確率変数Xが従うベルヌーイ分布の確率pというパラメータを推定していたことになります。
手元のデータをもとに、確率が最も高いパラメータを推定することを最尤推定と呼ばれています。

もう一つ重要な推定方法に、ベイズ推定と呼ばれる手法があります。
これはパラメータを一つの値として推定するのではなく、パラメータの分布を推定しようという方法です。
ベイズの定理を使うと、パラメータの事前（確率）分布からパラメータの事後（確率）分布を求めるということになります。

P(θ|X) = \frac{P(X|θ) * P(θ)}{P(X)}\\
P(θ)...事前（確率）分布\\
P(θ|X)...事後（確率）分布

そしてこの事前（確率）分布には、主観的な確率分布（例えば、寒波になる確率は、体感的に確率2/３のベルヌーイ分布に従いそうだなとか）を採用することができるのもベイズの特徴です。

最尤推定では、データ自体が確率変数である一方で、ベイズ推定はそのデータの発生を決めるパラメータが確率変数であると考えることになります。

(余談)頻度とベイズ

得られたデータのみからの情報を利用した法則性を導くことを頻度主義と呼ばれ、一方で事前にわかっている情報を取り込んで、法則性を導くことをベイズ主義と呼ばれたりします。
最尤推定とベイズ推定のように、データに対する扱い方が大きく異なっています。

現代の統計や機械学種では、上記の基礎事項で学んだ条件付き確率をベースに、ベイズの考えを取り入れた理論が多く存在します。
ベイズが採用される理由は、事前情報（確率）を取り込むことができるモデルであることが大きいと思います。

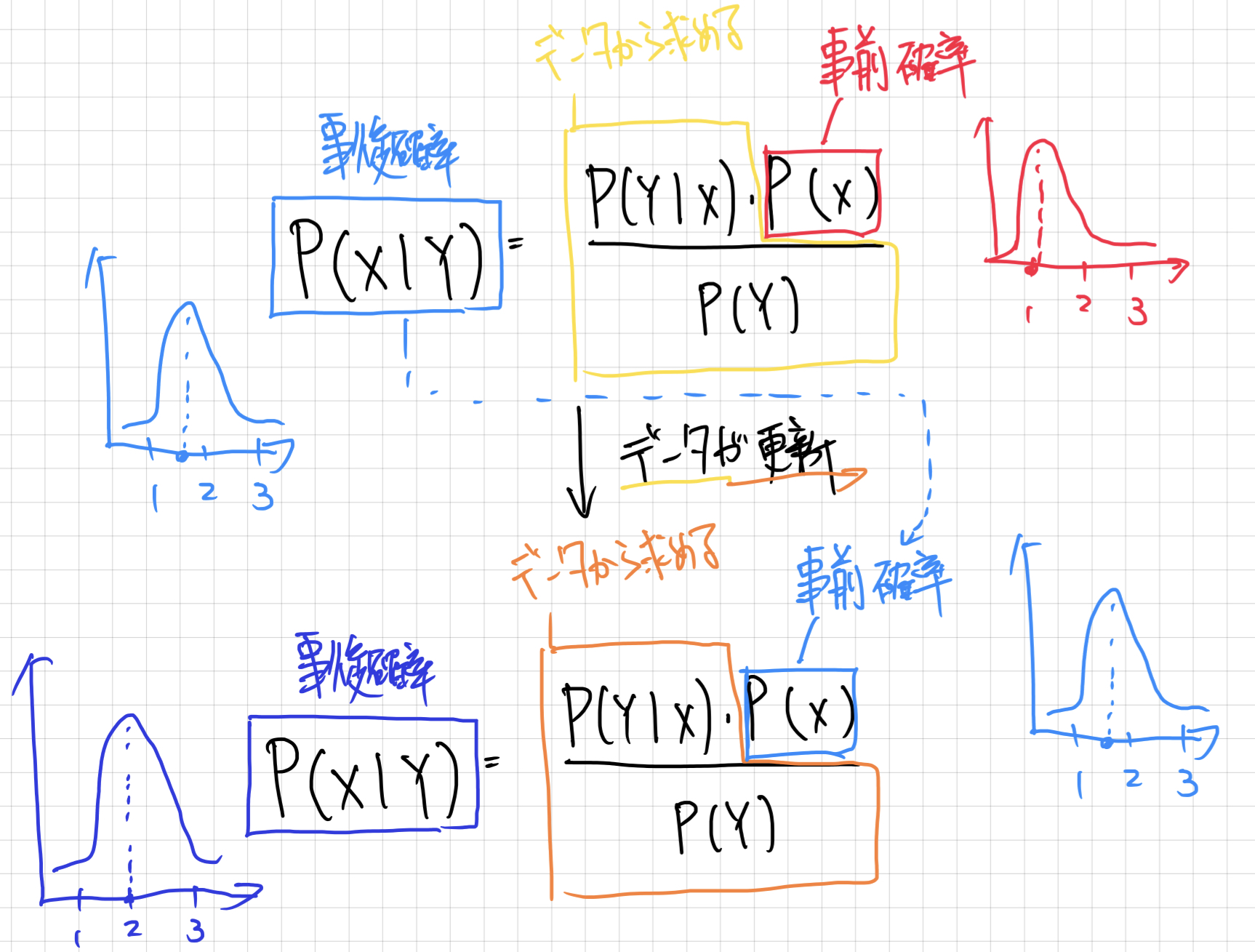
データが更新された場合、以前求めた事後確率を新たに、事前確率として利用することで新しい事後確率を求めることができることになります。

簡単に区別すると、最尤推定は、いまあるデータだけで真の法則性を求めていくのに対し、ベイズ推定は何度も更新することによって、真の法則性に近づけていくようなスタンスであると言えます。
だから、上記で少し説明したように、事前情報が主観的な確率であったとしても、いずれ真実に近づくであろうと考えていることになります。

ここで大事なのは、どちらが正しいかということではなく、今直面しているデータに対してどちらの考えを取り入れるかということです。
例えば、かなりデータ数が揃っているので、現時点で最尤推定でも十分な精度が出るという考えもありますし、まだデータ数が足りないので、ベイズ推定の更新で将来の精度を高めていこうというのも一つの考えだと思います。
この主義同士の論争は、今でもなお続いているそうです。だからこそ確率というものが複雑に感じてしまうのではないかと私は考えています。

2022年のQiita町の降雪とその後

今回の場合、最尤推定をした結果、60%の確率でQiita町には雪が降りそうだと推定できました。
そして、寒波がある場合は、80%まで確率が上がる可能性があることもわかりました。

今年はどうも寒波がくる予報なので、雪が降る確率がグッと高まりそうです。
いやいや、寒波ならもっと雪が確率が上がりそうだって？ベイズの視点から推定するとどうなるでしょうか。

ぜひいろんな確率の期待値を見積もって、楽しいクリスマスをお過ごしください。

統計や機械学習へ

確率がわかれば、統計と機械学習の理論や数式の解釈にとても役立ちます。
私が知り得る範囲で活用先について書いてみます。

確率変数を柔軟に扱う

モデル自体に確率を導入するのではなく、式の一部に確率を用いることも多くあります。
例えば、線形回帰モデルのような場合、実際のデータの数値とモデルで求めた数値との差を誤差と呼び、この誤差を正規分布に従うことを仮定するようなことがあります。

Y = βX + ε \qquad ε \sim N(0, 1)

最近の有名なモデルだったら、Diffusion Modelという画像生成のモデルの中でも、画像にガウシアンノイズつまり正規分布に従うノイズ（値）が画像に足されていくような過程を実装していたりします。
※このように確率変数が時間と共に確率が変化する確率過程と呼ばれる事象も考慮していく場合もあります。

つまり、確率を駆使して意図的に値を散らばすことでうまくデータを生成できるようになります。

モデルの拡張(例：潜在変数モデル)

データには存在しない、潜在変数と呼ばれる変数でデータを解釈するモデルを潜在変数モデルと呼ばれています。
主成分分析やオートエンコーダといった分析手法がその一種で、データの要因やデータを要約する潜在変数を数学的に計算しています。

求める潜在変数は、データに応じて固定的な数値となってしまうので、潜在変数を確率変数として扱うことで、不確実性を取り込むことができるようになります。
そして、確率的主成分分析や変分オートエンコーダといった新しいモデルに拡張することができます。

統計検定

統計の分野を勉強すると、推定した結果が本当に正しいのかをチェックする段階があります。
これを検定と呼び、数学的なアプローチにより結論を導きます。
t分布やカイの二乗分布などの確率分布などを駆使し、平均や分散といった統計（推定）量が、ある幅に収まるかどうかを背理法を用いて結論を導き出します。

確率分布の形がわかると、確率変数（の幅）ごとの確率がわかる性質を利用して、ある確率変数の実現値がどれくらいありえるかを有意水準と呼ばれる確率を基準に判定することになります。

（外観）データサイエンスの世界

データを扱う世界はとても複雑みたいです。
私が思うデータサイエンスの外観は以下の通り。

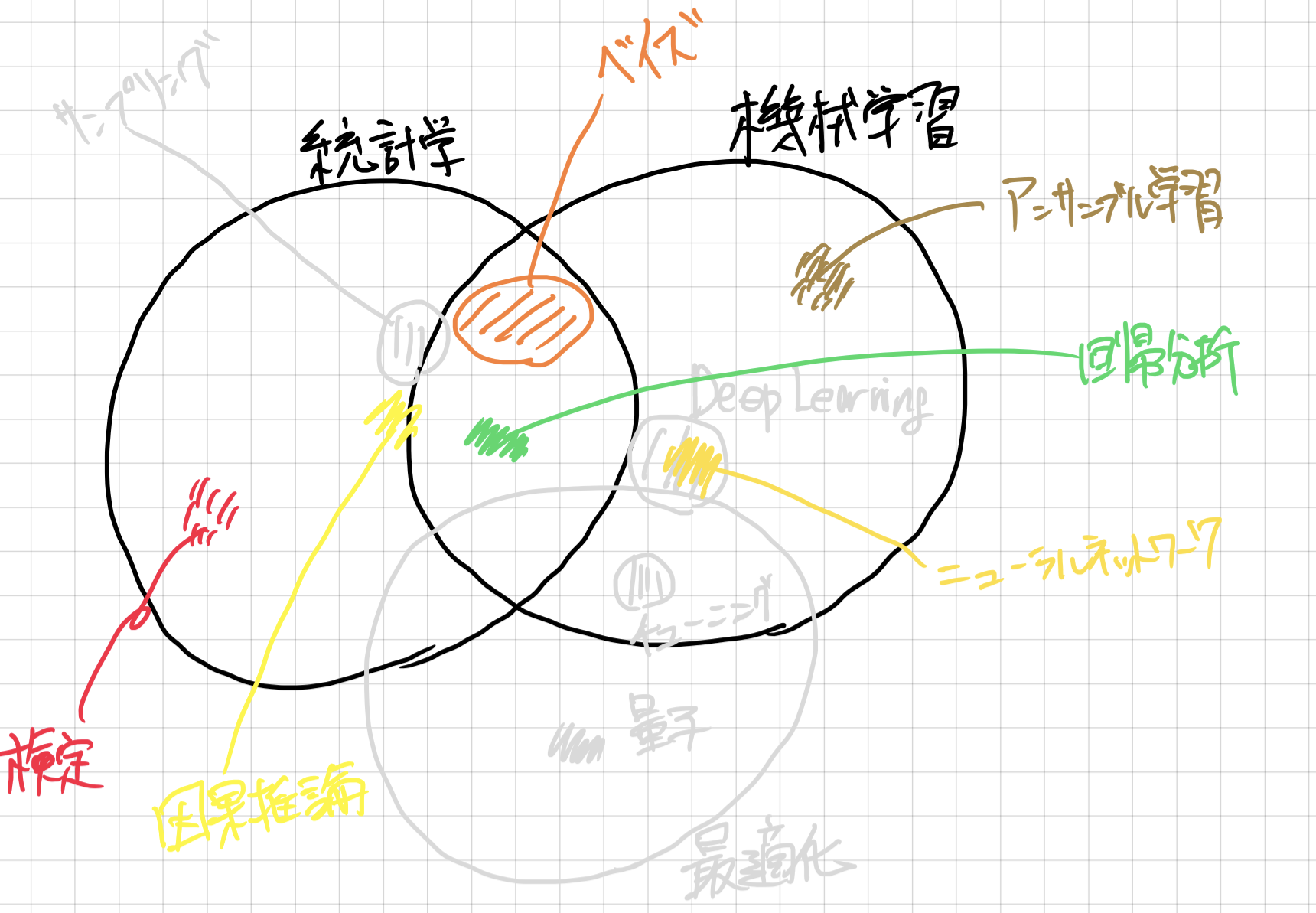
私もこの世界に飛び込んでみたばかりの新参者ですが、いろんな分野の学問や理論が重なりあい、この理論は機械学習だ、統計だ、最適化だと切り離せないことよくあって、いつも混乱してまうことがあります。
この記事もその辺りの表現が微妙なところがあると思います。

自分が直面している欲しい情報に対して有益な理論であれば、理論を分類するのは一旦おいて置き、理論を理解するための簡単なツールで掘り下げていくといいのではないでしょうか。

参考サイト

確率と統計

終わりに

弊社では、経験の有無を問わず、社員やインターン生の採用を行っています。

興味のある方はこちらをご覧ください。