他の記事
投球
他の球技にはあまりない特徴ではあるが、こと野球に関しては、投球時にボールの球速や回転(変化)をかなり左右できるようにする必要がある。
この形式が正解かどうかはわからないが、SnowballGameではこれを実現するために「ボールになる雪玉につけた名前に応じて変化球が投げられる」という形をとっている。
ボールが投げられたことの検知には、そのものずばりProjectileLaunchEventというイベントがあるためこれを用いる。このイベントが呼ばれた際にevent.getEntity().getShooter()としてやって、投げたプレイヤーのメインハンドの中身をチェックし、その名前と対応するようにボールの球速を変えてやればいい。(オフハンドからの投球にも対応するならば、メインハンドにあるものがボールではなくオフハンドにあるものがボールである場合にオフハンドをチェックすればいい。)
変化球に関してはBukkitRunnable.runTaskTimer(delay, period)を用いる。ふつうはディレイ0、ピリオド1で実行することになるだろう。投げられたボールのエンティティ自体と変化の向き・変化量を受け取って毎tickボールのvelocityを変えてやるように書けばいい。
ただし、ボールの変化の向きを求めるときに少し気を付けなくてはいけないことがある。
縦の変化に関しては確実にY方向の変動で表せるのだが、横の変化はそのとき投げたプレイヤーが向いている向きによって異なる。マウンドから見てホームベースがX方向にあることもあればZ方向にあることもあり、もっと言えば斜め向きの球場だってありうるわけだから、そうしたさまざまなバリエーションの球場でプレイヤーが違和感なく変化球を使えるようにしてやらなければいけない。
そのため、横の変化の向きはLocation.getDirection()を用いる。プレイヤーの現在の視線の向きを前と定めてしまえばいい。
//moveは符号が正の時1tickあたりのシュート方向への変化量を、負の時スライダー方向への変化量を表す
static Vector getHorizontalMove(Player player, double move, boolean fromMainHand){
//左投げの時は横変化の向きを逆にする
int modifierWithHand = 1;
if(player.getMainHand() == MainHand.LEFT && fromMainHand || player.getMainHand() == MainHand.RIGHT && !fromMainHand){
modifierWithHand = -1;
}
Location loc = player.getLocation();
//メインハンド側に向かう向きはYawを+90°した向き
loc.setYaw(loc.getYaw() + 90 * modifierWithHand);
return loc.getDirection().normalize().multiply(move);
}
このようにプレイヤーのLocationのYawを+90度してdirectionを取得してやることで、プレイヤーの「真右」の向きが得られる。
あとは変化球の種類と投球腕によって90の符号を変えてやればいい。ちなみにSnowballGameでは、コンフィグファイル内で「どういった名前をつけるとどういう変化をするか」を設定できるようにしている。
問題点
投球に関してはこの実装でほとんど問題はないのだが、ほかの野球ゲームとは違い、Minecraftでは変化球をいくらでも自由な向きに投げられるために、このままでは違和感のある挙動が発生することがある。
例えば真上にフォーシーム(上方向へ変化するボールとして設定されているとする)を投げたような場合に、本来フォーシームはバックスピンのボールであるため期待する挙動は投手から見て後ろへ後ろへ変化していくものなのだが、この実装では上下方向への変化は一律にY座標に関する変動と定義しているため、ひたすら真上に上がり続けてなかなか落ちてこない、といった挙動になってしまう。
これだけであればまあ実際のゲームではあまり影響もなく、「ゲームなのだから」「たかだかプラグインなのだから」で片づけてしまっても問題はないのだろうが、この変化球の実装を打球のほうにも適用しようとするときに問題が起こる。
キャッチャーフライが戻ってこないのである。
詳しい方法は後述するが、野球プラグインを標榜する以上、打撃の質に応じて打球にも「伸び」や「スライス」といった軌道の変化を当然与えたいものだ。その実現のためには打撃の瞬間に変化の方向を決定し、変化球の実装のために用いたのと同じBukkitRunnableを用いたい。そうすると、本来バックスピンがかかっているべきフライは単に毎Tick上へと変化するフライになってしまう。ということは、極めて強いバックスピンのかかるはずのキャッチャーフライは単に「なかなか落ちてこない」だけのフライになってしまう。
これではいけない。キャッチャーフライは、バックネット側を向いて捕るものである必要がある。
あの独特の取りづらさを表現できないのはあまりにも寂しい。
解決策
この問題に対する解決策としては、簡単な流体力学の知識が役に立った。
流体中を回転しながら進む円筒体・球体には、その運動のベクトルの回転ベクトル(回転のベクトル表現)との外積に比例する方向に揚力が発生するらしい。これをマグヌス効果というのだそうだ。藤川球児の全盛期によく耳にしたような気もする。
自分は高校物理すら受講していない人間なのでベクトルの外積と言われてもいまだにピンとこないが、フレミングの左手の法則のあれを右手で作った時、人差し指の方向に進みつつ、親指を軸に反時計回りに回るような回転をしているボールは、中指のほうに曲がっていくということらしい。やってみると、確かに上方向にバックスピンのボールが進んでいるときは後ろ方向に変化していき、上がりきって落ちて来るときには前へ前へ変化していくということになる。
また、変化量は回転量やその瞬間の球速といったものに依存することになる。具体的には、だいたいボールの直径を73mm、大気の状態が標準状態として、1Tickあたり1/8 * Math.PI * Math.PI * 1.205 * Math.pow(73 / 1000, 3) * velocity.length() * rpsくらい(参考)になるらしい。(rpsは一秒当たりの回転数。トラックマンとかでよく見るのは大体RPMが単位なので注意。)
つまり、
import org.bukkit.entity.Projectile;
import org.bukkit.scheduler.BukkitRunnable;
import org.bukkit.util.Vector;
public class BallMovingTask extends BukkitRunnable {
private Vector spinVector;
private Projectile ball;
private int rps;
public BallMovingTask(Projectile ball, Vector spinVector, int rps) {
this.ball = ball;
this.spinVector = spinVector;
this.rps = rps;
}
@Override
public void run() {
//バウンドしたり打たれてボールが死んだらタスクをキャンセルする
if(ball.isDead()){
this.cancel();
}
Vector velocity = ball.getVelocity();
if(spinVector.length() != 0){
Vector actualMove = velocity.getCrossProduct(spinVector);
if(actualMove.length() != 0){
actualMove.normalize().multiply(1/8 * Math.PI * Math.PI * 1.205 * Math.pow(73/1000, 3) * velocity.length() * rps);
}
velocity.add(actualMove);
}
ball.setVelocity(velocity);
}
}
といったRunnableを作り、投球するときにrpsとspinVectorを求めて渡してやればいいということになる。
ただし、SnowballGameでは「1tickあたりの変化量と変化の向きをコンフィグで決められる」という特徴のほうを重視して、「コンフィグの数値をもとに投球プレイヤーから見た変化の方向を求めたのちそれとボールの投げ出されたベクトルの外積をとって回転ベクトルとして用いる」「変化の量の値をspinVectorの長さとして持たせ、actualMoveをその長さに合わせる(なので上記の式を用いない)」という形になっている。
いずれにせよ、これでキャッチャーフライはきちんと戻ってくるし、スライスがかかったフライは失速しやすくなる。
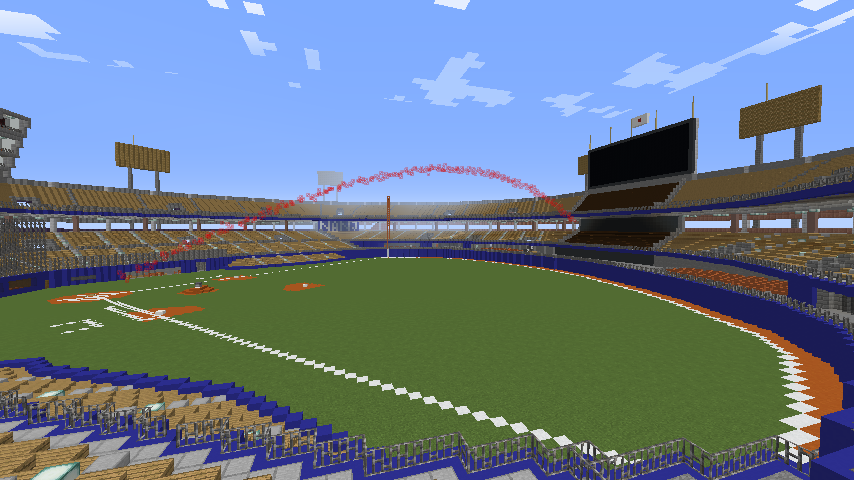
この計算方式にしたことで、ホームランの軌道が対称な放物線でなくなるのも特徴だ。
打撃
実情に詳しいわけでは全くないが、野球ゲームにおいて最も実装に個性が出るのが打撃の部分ではないだろうか。
厳密に打撃の再現をしようとすれば、バットの形を定義したうえで飛んでくるボールとの当たり判定を行う必要があるが、Minecraftでそれを実装するのはなかなか難しいものがある。では、どういった要素を満たしていれば「打撃が再現できている」とプレイヤーに感じてもらえるのだろうか。
野球における打撃を構成する要件として、
- タイミングとコースを合わせないと空振りしたり打球が弱くなったりする
- 打球の飛ぶ方向や高さがさまざまである
- スイングの強さを調節できる
といったものがあるのではないだろうか。これらを満たすため、SnowballGameでは弓をバットとして利用している。
弓は引きの強さというゲージをもともと持っているため、強さの調節が非常に簡単に可能だ。また、SpigotにはEntityShootBowEventがあり、プレイヤーが弓を放ったことを検知できる。また、このイベントはevent.setCancelled(true)したとしても放つはずだった矢のエンティティを取得することができ、この矢をそのままバットに見立てEntity.getNearbyEntities(x, y, z)を行って返り値の中にボールのエンティティがあるかどうかを判定することで、ボールとバットの当たり判定が行えるのである。
ここまででスイングの強さと空振りする/当たるの判定は可能になった。あとはバットに当たったボールがどんな打球になるかの問題だけをクリアすればいい。
これには、Location.subtract(Location)を用いて「バットに見立てた矢からボールがある位置までのベクトル」を求めて使うこととした。バットを振った位置より上にボールがあればフライに、外側にボールがあれば流し打ちになる。加えて、振り遅れてボールのほうが後ろにあるような場合にはバックネット方向に飛ぶファールになる。概ね感覚に近い挙動になってくれる。
打球の強さは、矢からボールが遠ければ遠いほど弱くなるようにしてやればよい。そうなるように調整する方法はいくつもあるだろうが、SnowballGameではバットからボールまでのベクトルをNormalizeしたうえでMath.pow(1.3, -batToBall.length())をかけるという方法をとっている。1以上の数値の-x乗は、xが0のときに1になりxが増えるごとに連続的に小さくなってくれ負の数になることがないため、想定外の数値になりづらく扱いやすい。
以上のようなことを踏まえると、
//EntityShootBowEventからgetBattedBall(event.getEntity(), event.getProjectile)の形で呼ぶ
static Projectile getBattedBall(Projectile arrow, float force){
//ボールとバットが当たる範囲は簡略化のため一律1.2とする
Collection <Entity> nearByEntities = arrow.getNearbyEntities(1.2,1.2,1.2);
for(Entity entity : nearByEntities){
if(Util.isBall(entity)){
Vector batToBall = entity.getLocation().subtract(arrow.getLocation()).toVector();
//ここの3.5はだいたいいい感じでホームランが出るくらいの値。特にこれを導出できる根拠はない。
double speed = Math.pow(1.3, -batToBall.length()) * force * 3.5;
Projectile battedBall = (Projectile)entity.getWorld().spawnEntity(entity.getLocation(), EntityType().Snowball);
battedBall.setShooter(arrow.getShooter());
battedBall.setVelocity(batToBall.normalize().multiply(speed));
return battedBall;
}
}
return null;
}
というようなものになる。あとは「投球の球速が速いほど飛距離が出やすく」「バットに当たる範囲はYを気持小さく」みたいな味付けを載せていけばいい。
問題点
この方式における一つ目の問題点は、上の投球のところをじっくり読んでいた方ならすぐにわかるかもしれない。つまり、打球の回転を設定するのが難しいことだ。
バットの曲率とボールの弾性から衝突時のボールの状態をシミュレートして…とやればあるいは求められるのかもしれないが、そんな難しい計算はとてもやりたくない。
せっかく「バットとボールとの位置関係」という打球の回転を定義するのにも使えそうな要素が求められているのだから、これを使いたい。では投球のところの最後で説明したのと同じ方法で打球の進行方向とバットからボールへのベクトルの外積を取って…とやりたいところだが、これもできない。その二つのベクトルは長さだけが違う同じ向きのベクトルだからだ。平行なベクトル同士の外積は常に零ベクトルになってしまう。(ジャイロボールが大体縦スライダーになる理屈とおなじ)
もう一つの問題は以前自分が動画を作成しているのでよければ見ていただきたい。
要するに、「速い打球速度と高い打球角度」を両立した打球が生まれないということである。
矢の位置よりボールが高い状態で打てば高いフライになるが距離が離れた分打球速度が落ち、矢がボールの近くになるように打てば打球速度は速くなるが低い角度の打球になる。これはゴロでも同じで、地面に深い角度で突き刺さり高く跳ね上がるようなゴロが生まれにくくなる。つまり打球が多様性に乏しくなってしまっているのである。
では、これらの問題をどのように解決していけばいいのか。
スイング軌道の実装
SnowballGameでは、その解決策として「スイング」のベクトルを定義し、打撃の際に打球のベクトルにそれを加えるという方法をとった。
こうすれば、打球の運動のベクトルはバットからボールのベクトルとは違う向きを向くことになり、二つのベクトルの外積をとって打球の回転ベクトルにすることができる。
また、打球の多様性もスイング軌道を操作することで確保できる。アッパースイング・ダウンスイングなど打者ごとに個性を出せるようにできればなおよい。
では問題はその「スイング軌道」をどうやって定義するかである。このプラグインの中でも最も似非なポイントがここであると自分でも思っているのだが、自分の経験や過去に読んだ技術書などから、野球におけるスイングは以下の3つの運動から構成されていると自分は考えた。
- 腰の回転による地面と平行な回転運動
- 肩甲骨とかで作る上下運動
- 斜め後ろ方向に腕を伸展させる運動
この分類が正しいとは限らないが、SnowballGameにおいてはこれに基づいてスイング軌道が実装されている。
この三つのうち、最も難易度が高いのは二つ目の運動である。この動きは「アッパー・レベル・ダウン」といったスイングを形容する言葉の対象になる部分そのものであり、なおかつその上下動の振れ幅、変動の具合もそれぞれの打者ごとに異なる。つまり「これが正解」という軌道が存在しないのである。
ただし、強引な理屈を押し通せば「理想」といえなくもない軌道は存在する。それは、最速降下曲線というものである。
要するにこれは「平面上のある点からある点まで重力のみが作用して移動する場合に一番速く到達する」軌道であるらしい。つまり、「スイングにかかる時間はできるだけ短いほうがいい」という仮定をするのであれば、これが理想のスイング軌道だといえるということになる。本当はバットを振る運動は「重力のみが作用する運動」ではないためそれでも怪しいのだが、少なくともゲームに用いるための目安として使う分には問題ないだろう。(先日某番組で「大谷翔平のスイング軌道はサイクロイドである」という特集が組まれたということを耳にした。この最速降下曲線はサイクロイドになるらしいので、ある程度現実に即したものであると考えていいようだ。)
二次元平面上の最速降下曲線はx=a(θ-sinθ), y=a(1-cosθ)という風になるそうなので、このxの式をX,Zの座標に、yの式をYの座標に当てはめていけばいい。
問題はこの曲線を伸ばしていく向きだが、これは上記の3つ目の運動と組み合わせて考え、斜め後ろ方向(右打者の場合視線から右方向に90度回転させた方向)に伸ばしていくものとする。
なので、
// 今後実装する横方向の回転の度合いをrollとしている。
// rollDirectionは右打者であれば1,左打者であれば-1となる。
public static Location getBatPosition(Location eye, double roll , int rollDirection){
Location eyeLoc = eye.clone();
eyeLoc.setYaw(eyeLoc.getYaw() - (float)(90 * rollDirection));
Vector push = eyeLoc.getDirection().setY(0).normalize();
double theta = Math.abs(roll * 2);
double x = push.normalize().getX() * (theta - Math.sin(theta));
double y = -(1 - Math.cos(theta));
double z = push.normalize().getZ() * (theta - Math.sin(theta));
return eye.clone().add(x,y,z);
}
と書ける。これを用いてrollに0-πまでの数値を与え、得られた位置にパーティクルをスポーンさせるというループを20回実行すると、こんな感じになる。
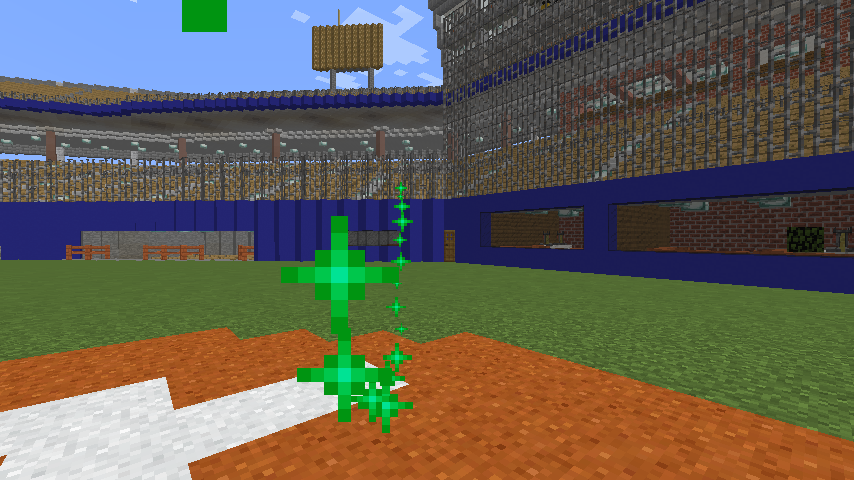
ここまでくれば、あとは二つ目の運動である水平方向の回転を実装すればいい。
実をいうと、今ここを書き始めるまで自分は座標変換を用いてこの回転を実装していたのだが、この記事を書いてやっていることを整理しているうちに、**「Yawを変えればいいだけだ」**と気づいてしまった。気づいてみると当たり前のことなのに、なぜ今まで分からなかったのか…
public static Location getBatPosition(Location eye, double roll , int rollDirection){
Location eyeLoc = eye.clone();
// ↓ここを変えるだけでよかった…
eyeLoc.setYaw(eyeLoc.getYaw() - (float)(90 * rollDirection) - Math.toDegrees(roll));
Vector push = eyeLoc.getDirection().setY(0).normalize();
double theta = Math.abs(roll * 2);
double x = push.normalize().getX() * (theta - Math.sin(theta));
double y = -(1 - Math.cos(theta));
double z = push.normalize().getZ() * (theta - Math.sin(theta));
return eye.clone().add(x,y,z);
}
で、さっきと同じようにパーティクルを出してみたのがこれ。
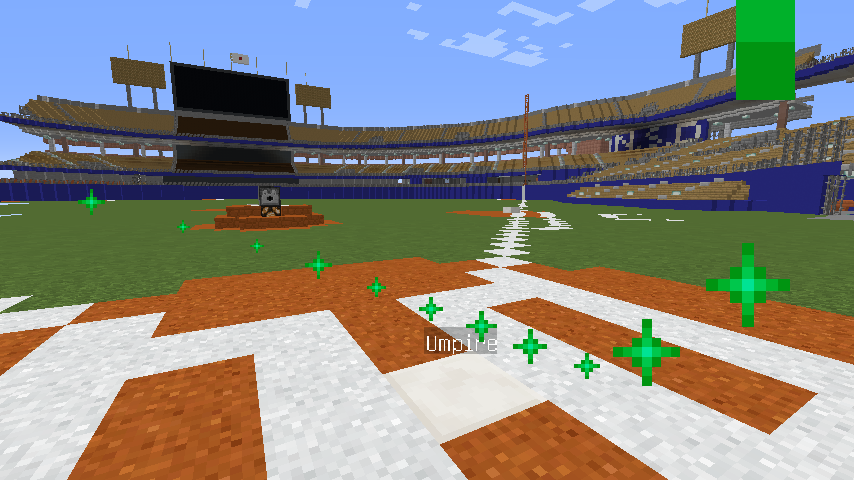
右に90度ずれた方向からスイングが始まっているので、視線が向いている方向つまりミートポイントとなる方向はrollがπ/2になるところである。thetaはrollの絶対値の2倍なので、そのときYが最低値を取るようになっている。
このパーティクルを見るとスイングしている位置が体から遠すぎるように見えるかもしれないが、このスイング軌道は当たり判定には用いられないため問題ない。当たり判定に関しては上記の矢の位置とボールの関係のみが用いられ、このスイング軌道はバットがボールに当たった場合にバットからボールに与えられる力を計算するためだけに使われる。
その部分は、
//視線のある位置でボールをミートし、そこから0.01ラジアン(この数字に根拠はない)だけ回転した位置までボールとバットが接触していたものとしている
Vector batMove = getBatPosition(player.getEyeLocation(), (Math.PI / 2 + 0.01) * rolld, rolld,).subtract(getBatPosition(player.getEyeLocation(), Math.PI / 2 * rolld, rolld,));
といった感じでいいだろう。
副産物
このような形でスイング軌道を表現したことで、「アッパースイング・ダウンスイングをどう定義するか」という問題も簡潔に解決できるようになった。
上記のgetBatPosition()には、rollとthetaという二つの角度を表す変数が存在する。rollがスイング開始位置からの水平方向の回転で、thetaが最速降下曲線を描くために用いられている円の回転具合である。
先程も説明したように、thetaがrollの二倍に等しい場合、ボールをミートするポイントは最速降下曲線上の最低地点になる。その時点よりも前は上から下への軌道になっていて、その地点よりも後ろなら下から上への軌道になるという地点でミートしているということになる。つまり、これを「レベルスイング」と定義してしまえるのではないだろうか。
ということは、ここよりも前の時点にボールのインパクトのポイントがあればダウンスイング、後にあればアッパースイングというように表現することができるようになる。つまり、thetaに何らかの数値を加えれば加えた数値だけアッパースイングに、減じれば減じた分だけダウンスイングになるといえる。ということは、
public static Location getBatPosition(Location eye, double roll , int rollDirection, double upper){
Location eyeLoc = eye.clone();
eyeLoc.setYaw(eyeLoc.getYaw() - (float)(90 * rollDirection - Math.toDegrees(roll)));
Vector push = eyeLoc.getDirection().setY(0).normalize();
// 1を超えるとサイクロイドが一周してしまうため
if(Math.abs(upper) > 1){
upper = 1 * Math.signum(upper);
}
// upperはコンフィグで設定できる値にしたいので、分かりやすくするためにπの倍率にしておく
double theta = Math.abs(roll * 2) + Math.PI * upper;
double x = push.normalize().getX() * (theta - Math.sin(theta));
double y = -(1 - Math.cos(theta));
double z = push.normalize().getZ() * (theta - Math.sin(theta));
return eye.clone().add(x,y,z);
}
このように書いてやれば、upperの値が大きいほどフライが打ちやすく、(符号が負で)小さいほどゴロが打ちやすくなる。こうしておけば、変化球と同様の仕組みで「どの名前のバットを使うとどういったスイングになるか」ということをプレイヤーがコンフィグで設定できるようになる。よりカスタマイズ性を高められたといえる。
また、この条件で計算したバットからボールへの力は、打者にとっての「引っ張り」の方向になる。
そのためこれをボールに加えると、「引っ張り」方向への打球が最も飛距離が出やすいということになる。より現実に近い打撃が可能になったと言えるのではないだろうか。
続き
次の記事では捕球の部分と他の球技の実装のために使えそうなTips的なものについて書く予定。