はじめに
実験データの解析等でMATLABを用いてる方であれば、手元のデータに対して特定の関数でフィッティングを行いたいという場面が日常的にあると思います。本記事では非線形モデルを用いて実験データのフィッティングを行うことを想定して、近似値を取得する際に使用する関数の違いについて検証します。尚、当方回帰分析などの分野は専門外でアルゴリズムなどの深い部分については理解しておりませんので、その点ご容赦ください。
この記事でわかること
MATLABで非線形モデルを用いたフィッティングに使用できる関数の種類
MATLABで非線形モデルを用いたフィッティングを行う方法
使用環境
Windows10, MATLAB R2022a
本記事では以下の Toolbox を使用しています。
- Curve Fitting Toolbox
- Optimization Toolbox
- Statistics and Machine Learning Toolbox
- Symbolic Math Toolbox(番外編)
使用するモデル
本記事では非線形モデルの例としてガウシアンを扱いたいと思います。フィッティングに使用するデータは以下の式に従うものとします。
y = a\exp-\left(\frac{x-b}{c}\right)^2 + d
a = 10,\,b = 50,\,c = 10,\,d = 0.5
フィッティングするデータの生成
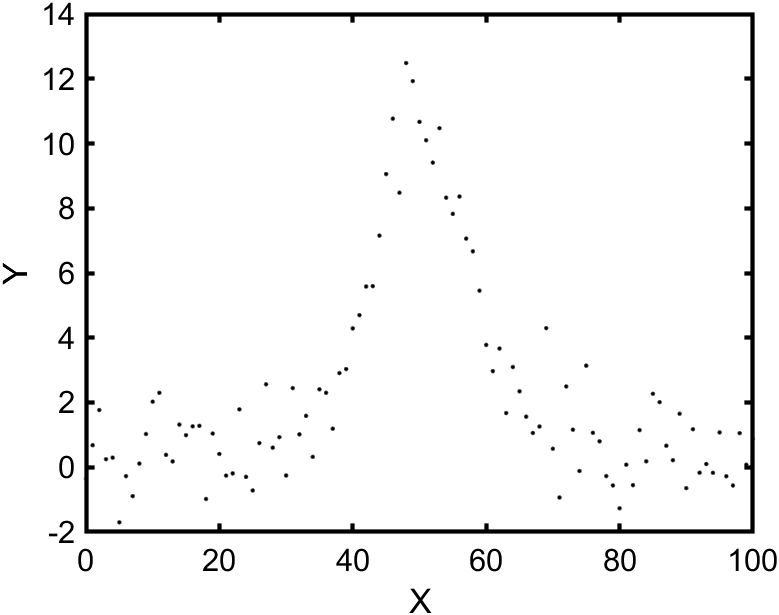
フィッティングするデータを生成します。ここでは randn を用いてデータにゆらぎを加えています。
% variable
xData = 0:100;
% coefficient
a = 10;
b = 50;
c = 10;
d = 0.5;
% make data
getYData = @(x) a*exp( -((x-b)/c).^2 ) + d;
y = getYData(xData);
yData = y + randn(1,length(xData));
[xData, yData] = prepareCurveData(xData, yData);
%% data plot
fig = figure(1);
fig.WindowStyle = "docked";
plot(xData,yData,".k");
xlabel("X");
ylabel("Y");
フィッティングの実行
任意の非線形モデルを使用できる fit, lsqcurvefit, fitnlm の3つの関数を使って生成したデータをフィッティングしました。
今回フィッティングのアルゴリズムは レーベンバーグ・マーカート法 というものに統一しています。また初期条件も同じ値を使用しています。
fit 関数
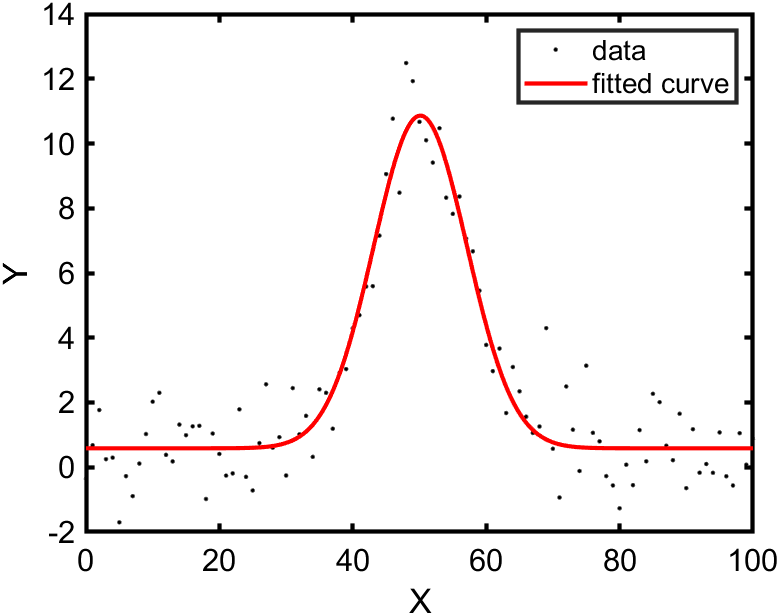
まず Curve Fitting Toolbox に入っている fit 関数を用いてフィッティングをしてみます。
曲線または曲面によるデータへの近似 - MATLAB fit - MathWorks
% fitting by "fit"
ft = fittype( 'a*exp( -((x-b)/c)^2 ) + d', ...
'independent', 'x', 'dependent', 'y');
opts = fitoptions( 'Method', 'NonlinearLeastSquares' );
opts.Algorithm = "Levenberg-Marquardt";
opts.StartPoint = [10 50 10 0.5];
[fit1,gof,output] = fit( xData, yData, ft, opts);
% make figure
plot(xData,yData,".k");
hold on
plot(fit1);
hold off
legend("data", "fitted curve");
xlabel("X");
ylabel("Y");
実行結果
fit1 =
General model:
fit1(x) = a*exp( -((x-b)/c)^2 ) + d
Coefficients (with 95% confidence bounds):
a = 10.27 (9.543, 11.01)
b = 50.13 (49.57, 50.69)
c = 9.905 (9.043, 10.77)
d = 0.5857 (0.3304, 0.8411)
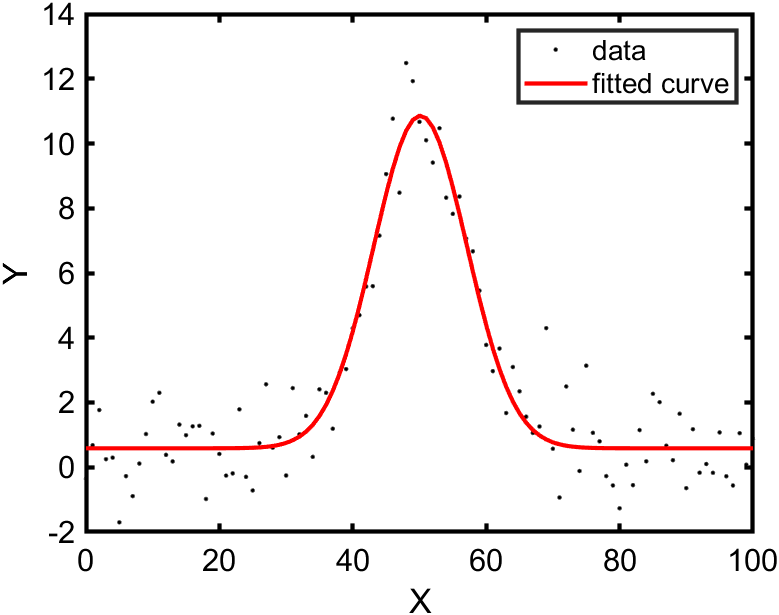
lsqcurvefit 関数
次に Optimization Toolbox に入っている lsqcurvefit 関数を用いてフィッティングをしてみます。モデルの指定方法、初期条件の与え方が fit 関数とは異なります。
MATLAB lsqcurvefit - MathWorks 日本
% fitting by "lsqcurvefit"
modelfun = @(b,x) b(1)*exp( -((x-b(2))/b(3)).^2 ) + b(4);
options = optimoptions('lsqcurvefit','Algorithm','levenberg-marquardt');
beta0 = [10 50 10 0.5];
[fit2,resnorm,residual,exitflag,output2] = lsqcurvefit(modelfun,beta0,xData,yData,[],[],options);
% make figure
plot(xData,yData,'.k')
hold on
plot(xData,modelfun(fit2,xData),'r')
hold off
legend("data", "fitted curve");
xlabel("X");
ylabel("Y");
実行結果
fit2 =
10.2743 50.1285 9.9053 0.5857
fitnlm 関数
最後に Statistics and Machine Learning Toolbox に入っている fitnlm 関数を用いてフィッティングをしてみます。決定係数や標準誤差をわかりやすい形式で表示してくれます。
非線形回帰モデルの当てはめ - MATLAB fitnlm - MathWorks 日本
% fitting by "fitnlm"
modelfun = @(b,x) b(1)*exp( -((x-b(2))/b(3)).^2 ) + b(4);
beta0 = [10 50 10 0.5];
fit3 = fitnlm(xData,yData,modelfun,beta0);
% make figure
plot(xData,yData,".k");
hold on
plot(xData,predict(fit3,xData),"r");
hold off
legend("data", "fitted curve");
xlabel("X");
ylabel("Y");
実行結果
fit3 =
Nonlinear regression model:
y ~ F(b,x)
Estimated Coefficients:
Estimate SE tStat pValue
________ _______ ______ ___________
b1 10.274 0.36852 27.88 4.1722e-48
b2 50.128 0.28111 178.32 6.8457e-124
b3 9.9053 0.43454 22.795 9.6991e-41
b4 0.58575 0.12867 4.5525 1.5392e-05
Number of observations: 101, Error degrees of freedom: 97
Root Mean Squared Error: 1.03
R-Squared: 0.906, Adjusted R-Squared 0.903
F-statistic vs. constant model: 312, p-value = 1.11e-49
フィッティング結果の比較
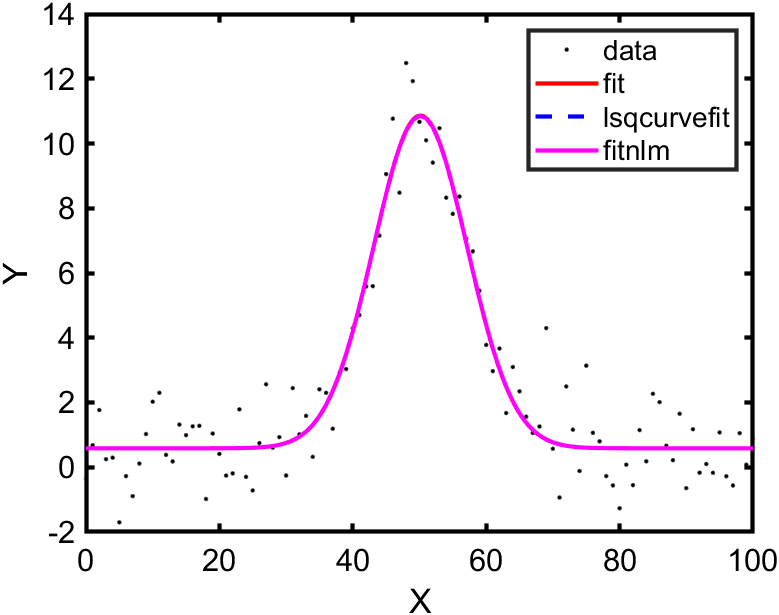
フィッティングにより求まった係数の値は以下の通りです。いずれの係数も関数の違いによらず有効数字3桁以上まで一致していることがわかります。
| 係数 | fit 関数(95% 信頼区間) | lsqcurvefit 関数 | fitnlm 関数(標準誤差) |
|---|---|---|---|
| a | 10.27 (9.543, 11.01) | 10.2743 | 10.274 (0.36852) |
| b | 50.13 (49.57, 50.69) | 50.1285 | 50.128 (0.28111) |
| c | 9.905 (9.043, 10.77) | 9.9053 | 9.9053 (0.43454) |
| d | 0.5857 (0.3304, 0.8411) | 0.5857 | 0.58575 (0.12867) |
それぞれのフィッティング結果を重ねて表示すると次のようになりました。
やはり関数によらずフィッティング結果は一致しています。
まとめ
今回は同一のデータおよびモデルを用いたフィッティングで、関数の種類のみを変えて結果に差が出るのか検証してみました。結果として今回の場合ではフィッティング結果は関数の種類によらずほぼ一致しました。よって、基本的には使いやすいと感じたものを選択すればよいと考えています。
番外編
番外編といいつつ実はこの記事を書こうと思った最大の理由だったりしますので、興味ある方はお付き合いください。
個人的な話ですが私はこれまでデータに対するフィッティングは fit 関数を主に使っていました。しかしながら、とある理由から今後は fitnlm 関数を使っていこう と思っています。その理由について簡単に紹介しますので参考にしてください。
結論から述べると、 今後 fitnlm を使っていこうと考えた理由は fit, lsqcurvefit ではフィッティングができない (と現時点では思っている) モデルがあったためです。式の意味や詳細については省略しますが次のようなモデルです。
y = a \frac{Li_2\left( -f \exp -\left(\frac{x-b}{c}\right)^2 \right)}{Li_2(-f)} + d\\
Li_s(z) \stackrel{\mathrm{def}}{=} \sum_{k=1}^{\infty}\frac{z^k}{k^s}
$Li_s(z)$ は多重対数関数という特殊関数で Symbolic Math Toolbox に polylog 関数として用意されています。
多重対数 - MATLAB polylog - MathWorks 日本
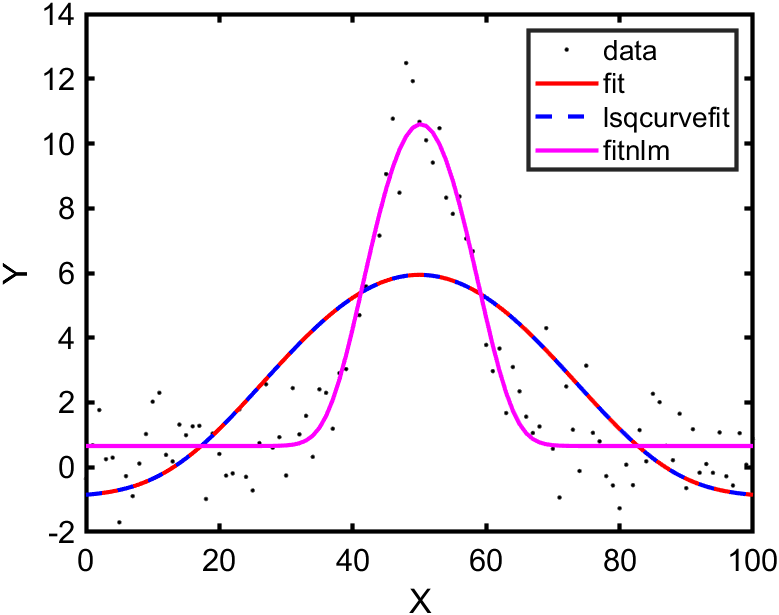
理論的にはこの関数を用いてもガウシアンフィッティングが可能です。そこで本記事で使用したデータに対してこの特殊関数のモデルでフィッティングをしてみました。fit, lsqcurvefit, fitnlm それぞれを用いて求めたフィッティング結果を重ねて表示すると次のようになります。
コード
ft = fittype( 'a*real( polylog(2,-f*exp( -((x-b)/c)^2 ))/polylog(2,-f) ) + d', ...
'independent', 'x', 'dependent', 'y');
opts = fitoptions( 'Method', 'NonlinearLeastSquares' );
opts.Algorithm = "Levenberg-Marquardt";
opts.StartPoint = [10 50 20 0.5 10];
[mdl1,gof1,output1] = fit( xData, yData, ft, opts);
modelfun_polylog = @(b,x) b(1)*real( polylog(2,-b(5)*exp( -((x-b(2))/b(3)).^2 ))/polylog(2,-b(5)) ) + b(4);
opts = statset;
options = optimoptions('lsqcurvefit','Algorithm','levenberg-marquardt');
beta1 = [10 50 20 0.5 10];
% Fit model to data
[mdl2,resnorm3,residual3,exitflag3,output3] = lsqcurvefit(modelfun_polylog,beta1,xData,yData,[],[],options);
mdl3 = fitnlm(xData,yData,modelfun_polylog,beta1,'Options',opts);
plot(xData,yData,".k");
hold on
plot(mdl1,"r");
plot(xData,modelfun_polylog(mdl2,xData),"--b")
plot(xData,predict(mdl3,xData),"-m");
hold off
legend("data", "fit", "lsqcurvefit", "fitnlm");
xlabel("X");
ylabel("Y");
ご覧のように fitnlm を用いたフィッティング結果はデータをある程度再現できていますが、lsqcurvefit, fitnlm を用いたフィッティング結果はデータからややずれているように見えます。初期条件の与え方を変えるとより明らかなのですが、実は関数 lsqcurvefit, fitnlm を用いてフィッティングした場合には係数 $c$ と $f$ についてのパラメータ探索が全く行われません。計算は収束するものの初期条件で与えた値がそのまま返ってきます。
この違いがアルゴリズムのどのような違いによって起こるのか、そもそもアルゴリズムの違いなのか(プログラムの書き方が悪い可能性もあると思っている)全く理解していませんが、とりあえずきちんと動くものを使おうという感じです。非線形モデルとしてガウシアンのような一般的な関数を用いる場合であればこの差は出てこないと思いますが、専門分野によっては特殊なモデルでフィッティングしなければならない場合も多々あるかと思いますので、どなたかの参考になれば幸いです。