【論文紹介】量子アニーリングで量子化学計算【Domain Folding】

1. はじめに

量子アニーリングで量子化学計算を行う手法について説明します。

量子ゲート方式で量子化学計算を行う手法は多く提案されています。
SSVQEと呼ばれる代表的な手法を以下の記事で説明しました。

• SSVQEを用いて励起状態との遷移行列を計算してみた。

量子ゲート方式は電子系のハミルトニアンと相性が良く、パウリ演算子を用いて各項を回路上で実装してその期待値を計算することでエネルギーを計算することが出来ます。

一方で量子アニーリング方式では古典的なイジングモデルしか扱えないので直接的に電子系のハミルトニアンを計算することが出来ません。

• 電子系のハミルトニアン
  (量子コンピューターで計算できるように変換した時の一般式)

\hat{\mathcal{H}}_e = \sum_{i,j,k,l} h_{i,j,k,l}\otimes_i \boldsymbol{I}_i \otimes_j \sigma_{jx} \otimes_k \sigma_{ky} \otimes_l \sigma_{lz}

• イジングモデル

\hat{\mathcal{H}}_{ising} = \sum_{i}h_i \sigma_{iz} + \sum_{i,j}J_{ij} \sigma_{iz}\sigma_{jz}

量子アニーリングマシンで最適化できるハミルトニアンには$\sigma_{ix}, \sigma_{iy}$を含むことは出来ません。
補助的に$\sigma_{iz}$を使用して$\sigma_{ix}, \sigma_{iy}$の振る舞いを再現する手法が次の論文で提案されています。

• Electronic Structure Calculations and the Ising Hamiltonian
• Solving Quantum Chemistry Problems with a D-Wave Quantum Annealer

2本目の論文の図2で水素原子(2電子4軌道)のハミルトニアンを実装するために必要な量子ビット数が示されています。

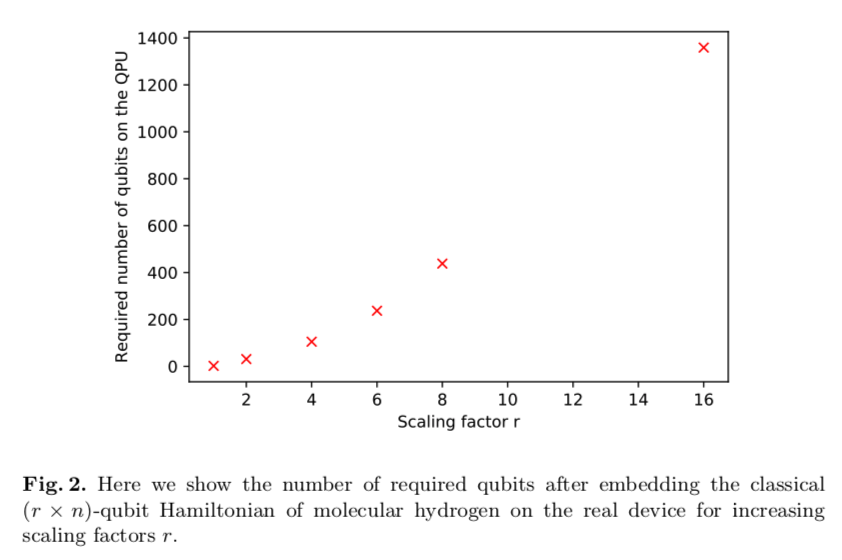
ここでは詳しく説明しませんがScaling Factor rは電子系のハミルトニアンをイジングモデルで表現する時の精度を調整するハイパーパラメータになります。
大きく設定した方が正確になりますがその分ビット数が指数関数的に増大します。
以下の図では設定したrの値で計算した時のエネルギー値と厳密解との比較を行っています。

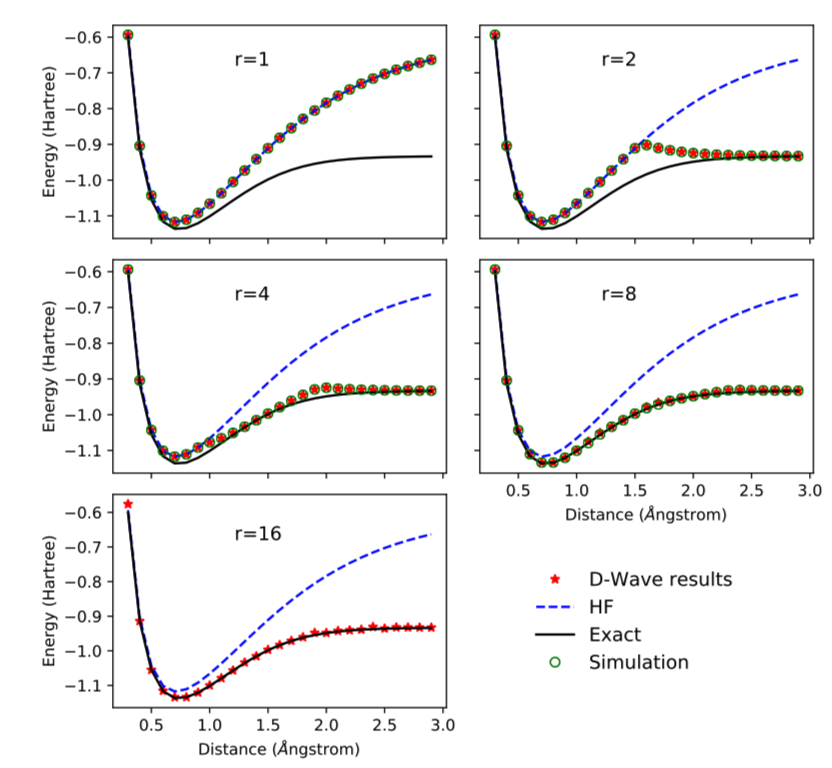
$r=16$で厳密対角化の結果と一致しています。
この時に必要となるビット数は約1400ビットになります。
ハートリーフォック近似と同程度の制度であれば$r=1$でも良いことが分かります。

今回は上記の論文のように直接電子系のハミルトニアンをQUBOで表現するのではなく、ハミルトニアンの符号のみを決定するQUBOを作成して量子アニーリングで解く手法についてレビューします。
この手法はDomain Foldingと名付けられておりOTIというカナダのベンチャー企業が開発しました。
論文は以下を参照して下さい。

• Quantum chemistry on quantum annealers

以下の解説は必ずしも正しいとは限りません。
間違いなどがあれば指摘お願いします。

2. 理論

SSVQEでも用いられている変分法を利用します。
こちらの記事でも紹介しましたが変分量子回路では変分仮設(Variational Ansatz)と呼ばれる量子状態を設定してハミルトニアンの期待値を最小化するような状態を求めます。

$$
\def\bm#1{\boldsymbol{#1}}
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\brakett#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
\def\braket#1#2#3{\bra{#1}#2\ket{#3}}
\min_{\boldsymbol{\theta}} \bra{\Psi(\theta)}\mathcal{H} \ket{\Psi(\theta)}
$$

SSVQEと同様に古典コンピュータと量子コンピュータで計算するパートが異なります。
上記の期待値を展開すると三角関数に関する項がたくさん出てきます。(後で詳しく説明しています。)
その三角関数の値を計算するために以下のような役割分担が行われます。

• 古典コンピュータ：三角関数の振幅の大きさを最適化する。 ($|\sin{\theta_i}|$)
• 量子コンピュータ：三角関数の符号を最適化する。($\text{sgn}(\sin{\theta_i})$)

Domain Foldingと呼ばれる手法を使ってハミルトニアンの期待値の展開式を上記の役割分担ができる形に変換していきます。

以下では細かい計算なども出てくるのでOverleafの計算ノートを参照していただいた方が見やすいかもしれません。

• Quantum Chemistry on Quantum Annealerの計算ノート

(SafariでQiitaの記事を見るとハット演算子が崩れる場合もあるようです。見にくかったら上のノートを参照してください。)

A. Electric structure problem

分子の電子状態を調べるには時間に依存しないシュレディンガー方程式

\begin{align}
    \hat{H}_e \Psi_i(\bar{\bm{r}} | \bar{\bm{R}}) = E_i(\bar{\bm{R}})\Psi_i(\bar{\bm{r}} | \bar{\bm{R}})
\end{align}

を解けばよい。電子と原子核の位置はそれぞれ

\begin{align}
    \bar{\bm{r}} &= (\bm{r}_1, \bm{r}_2, \dots, \bm{r}_{N_e}) \\
    \bar{\bm{R}} &= (\bm{R}_1, \bm{R}_2, \dots, \bm{R}_{N})
\end{align}

とする。$E_i(\bar{\bm{R}})$のことを**Potential Energy Surfaces(PESs)**と呼ぶ。
原子核の位置$\bar{\bm{R}}$によってハミルトニアンの係数の大きさが変化するため$\bar{\bm{R}}$の関数になっている。$\Psi_i(\bar{\bm{r}} | \bar{\bm{R}})$は電子の波動関数である。
第2量子化したハミルトニアンは

\begin{align}
    \hat{\mathcal{H}}_e = \sum_{ij}h_{ij}\hat{a}^{\dagger}_i \hat{a}_j + \sum_{ijkl}\brakett{ij}{kl}\hat{a}^{\dagger}_i \hat{a}^{\dagger}_j \hat{a}_k \hat{a}_l \tag{1}
\end{align}

となる。
$\hat{a}^{\dagger}_i, \hat{a}_i$は電子の生成消滅演算子である。また係数は

\begin{align}
    h_{ij} &= \int \psi^{*}_i(\bm{x})\biggl(-\frac{1}{2}\nabla^2_{\bm{r} }- \sum_{\alpha} \frac{Z_{\alpha}}{|\bm{r} - \bm{R}_{\alpha}|}\biggr)\psi_j(\bm{x})d\bm{x} \\
    \brakett{ij}{kl} &= \int \psi^{*}_i(\bm{x}_1) \psi^{*}_j(\bm{x}_2)\frac{1}{r_{12}} \psi_k(\bm{x}_1) \psi_l(\bm{x}_2) d\bm{x}_1 d\bm{x}_2
\end{align}

である。
$\psi_i(\bm{x})(i=1\sim N_{so})$は$\bm{x} = (\bm{r}, \sigma)$に依存するスピン軌道を表す基底関数である。
この基底でハミルトニアン$\mathcal{H}_e$を行列表示すると次元は$2^{N_{so}}\times 2^{N_{so}}$ になる。$\mathcal{H}_e$の固有ベクトルを**Full Configuration Interaction(FCI)**状態と呼ぶ。

この第2量子化したハミルトニアン$\mathcal{H}_e$はフェルミオンの生成消滅演算子で表現されている。
これを量子コンピューターで解くにはフェルミオンの演算子をパウリ演算子に変換する必要がある。
変換方法にはJordan-Wigner(JW)変換とBravyi-Kitaev(BK)変換の2種類が存在する。
いずれかの変換を施すと(1)は形式的に次のように表すことが出来る。

\begin{align}
    \hat{\mathcal{H}}_e = \sum_{I}C_I \hat{T}_{I} \tag{2}
\end{align}

$C_I$は$h_{ij}, \brakett{ij}{kl}$からなる係数で、$\hat{T}_{I}$は$C_I$に対応する演算子であり

\begin{align}
    \hat{T}_{I} &= \cdots \hat{\sigma}^{(I)}_{1} \hat{\sigma}^{(I)}_{0} \\
    &= \prod^{N_q}_{j=1}\hat{\sigma}^{(I)}_{j}
\end{align}

と一般的に表される。
$\hat{\sigma}^{(I)}_{i}$はi番目の電子に作用する演算子であり、$\bm{1}, \hat{\sigma}^{(x)}_{i}, \hat{\sigma}^{(y)}_{i}, \hat{\sigma}^{(z)}_{i}$のいずれかである。
この論文ではパウリ演算子$\hat{\sigma}^{(x)}_{i}, \hat{\sigma}^{(y)}_{i}, \hat{\sigma}^{(z)}_{i}$を$\hat{x}_i, \hat{y}_i, \hat{z}_i$と表している。

B. Quibit Coupled Cluster Method

Quibit Coupled Cluster(QCC)は2種類の変換を用いて試行関数・変分仮設を準備する。
1つ目がQubit Mean-Field(QMF)で、2つ目が電子間相互作用を取り入れるためのMulti-Qubit Unitary Transformationである。
まずはQMFについて説明する。

B.1 Qubit Mean-Field(QMF)

1つ目のステップでは変分仮説(Variational Ansatz)として

\begin{align}
    \ket{\bm{\Omega}} &= \prod^{N_q}_{i=1}\ket{\Omega_i} \\
    \ket{\Omega_i} &= \cos{\biggl(\frac{\theta_i}{2}\biggr)}\ket{0}_i + e^{\mathrm{i}\phi_i}\sin{\biggl(\frac{\theta_i}{2}\biggr)}\ket{1}_i \tag{3}
\end{align}

を準備する。
これは1電子の状態を個別にかけた状態である(エンタングルしていなくてそれぞれの電子状態が因数分解できることが重要)。$\theta$はブロッホ球の極角(天頂角)、$\phi$は方位角(偏角)に対応している。$\theta, \phi$の定義域は

\begin{align}
    \phi_i &\in [0, 2\pi) \tag{4}\\
    \theta_i &\in [0, \pi), \;\;\;(i=1,\dots, N_q) \tag{5}
\end{align}

である。
これらをまとめて$\bm{\Omega}= (\phi_i \theta_i )^{N_q}_{i=1}$と表し、

\begin{align}
    E_{\text{QMF}} := \min_{\bm{\Omega}}\bra{\bm{\Omega}} \hat{H} \ket{\bm{\Omega}} \tag{6}
\end{align}

を最小にする$\bm{\Omega}$を求める。
(6)に(3)を代入して具体的に式を書き下す必要がある。
論文ではこれを計算するにはハミルトニアン(2)に含まれるパウリ演算子に対して次の変換(直交座標を極座標に変換する時と同じ変換)

\begin{align}
    \hat{x}_i &\to \sin{\theta_i} \cos{\phi_i} \tag{7} \\ 
    \hat{y}_i &\to \sin{\theta_i} \sin{\phi_i} \tag{8} \\
    \hat{z}_i &\to \cos{\theta_i} \tag{9}
\end{align}

を施せば良いとのこと。何故この変換で良いのかについて説明する。

ハミルトニアン(2)の(3)による期待値を計算する。
(3)がそれぞれの電子状態に分解できる形をしているので、

\begin{align}
    \bra{\bm{\Omega}} \hat{H} \ket{\bm{\Omega}} &= \sum_{I}C_{I} \bra{\bm{\Omega}} \hat{T}_{I} \ket{\bm{\Omega}}  \\
    &= \sum_{I}C_{I} \prod^{N_q}_{i=1}\bra{\Omega_i} \hat{T}_{I} \ket{\Omega_i} \\
    &= \sum_{I}C_{I} \prod^{N_q}_{i=1} \prod^{N_q}_{j=1} \bra{\Omega_i} \hat{\sigma}^{(I)}_{j}\ket{\Omega_i} \\
    &= \sum_{I}C_{I} \prod^{N_q}_{i=1} \bra{\Omega_i} \hat{\sigma}^{(I)}_{i} \ket{\Omega_i} \tag{10}
\end{align}

となる。(10)に含まれるパウリ演算子の期待値$\bra{\Omega_i} \hat{\sigma}^{(I)}_{i} \ket{\Omega_i}$を計算すれば良いことが分かる。

まずは$\hat{x}_i$に対して

\begin{align}
    \hat{x}_i \ket{\Omega_i} &= \cos{\biggl(\frac{\theta_i}{2}\biggr)}\hat{x}_i \ket{0}_i + e^{\mathrm{i}\phi_i}\sin{\biggl(\frac{\theta_i}{2}\biggr)}\hat{x}_i \ket{1}_i \nonumber \\
    &= \cos{\biggl(\frac{\theta_i}{2}\biggr)} \ket{1}_i + e^{\mathrm{i}\phi_i}\sin{\biggl(\frac{\theta_i}{2}\biggr)}\ket{0}_i
\end{align}

となる。また、

\begin{align}
    \bra{\Omega}_i = \cos{\biggl(\frac{\theta_i}{2}\biggr)}\bra{0}_i + e^{-\mathrm{i}\phi_i}\sin{\biggl(\frac{\theta_i}{2}\biggr)} \bra{1}_i
\end{align}

である。これらと$\brakett{\alpha}{\beta} = \delta_{\alpha\beta}$より、

\begin{align}
    \braket{\Omega_i}{\hat{x}_i}{\Omega_i} &= e^{\mathrm{i}\phi_i}\sin{\biggl(\frac{\theta_i}{2}\biggr)}\cos{\biggl(\frac{\theta_i}{2}\biggr)}\brakett{0}{0} + e^{-\mathrm{i}\phi_i}\sin{\biggl(\frac{\theta_i}{2}\biggr)}\cos{\biggl(\frac{\theta_i}{2}\biggr)}\brakett{1}{1} \\
    &= \sin{\biggl(\frac{\theta_i}{2}\biggr)}\cos{\biggl(\frac{\theta_i}{2}\biggr)} \biggl(e^{\mathrm{i}\phi_i} + e^{-\mathrm{i}\phi_i}\biggr) \\
    &= \frac{1}{2} \sin{\theta_i}\times 2\cos{\phi_i} \\
    &= \sin{\theta_i}\cos{\phi_i}
\end{align}

となり、(7)と一致する。
同様に$\hat{y}_i$の期待値を計算する。

\begin{align}
    \hat{y}_i \ket{\Omega_i} &= \cos{\biggl(\frac{\theta_i}{2}\biggr)}\hat{y}_i \ket{0}_i + e^{\mathrm{i}\phi_i}\sin{\biggl(\frac{\theta_i}{2}\biggr)}\hat{y}_i \ket{1}_i \nonumber \\
    &= \cos{\biggl(\frac{\theta_i}{2}\biggr)} (i)\ket{1}_i + e^{\mathrm{i}\phi_i}\sin{\biggl(\frac{\theta_i}{2}\biggr)(-i)}\ket{0}_i
\end{align}

より、

\begin{align}
    \brakett{\Omega_i}{\hat{y}_i|\Omega_i} &= e^{\mathrm{i}\phi_i}\sin{\biggl(\frac{\theta_i}{2}\biggr)}\cos{\biggl(\frac{\theta_i}{2}\biggr)}(-i)\brakett{0}{0} + e^{-\mathrm{i}\phi_i}\sin{\biggl(\frac{\theta_i}{2}\biggr)}\cos{\biggl(\frac{\theta_i}{2}\biggr)}(i)\brakett{1}{1} \\
    &= \sin{\biggl(\frac{\theta_i}{2}\biggr)}\cos{\biggl(\frac{\theta_i}{2}\biggr)}(-i) \biggl(e^{\mathrm{i}\phi_i} - e^{-\mathrm{i}\phi_i}\biggr) \nonumber \\
    &= \frac{1}{2} \sin{\theta_i}\times(-i)\times 2i\sin{\phi_i} \nonumber \\
    &= \sin{\theta_i}\sin{\phi_i}
\end{align}

となり、(8)と一致する。
最後にに$\hat{z}_i$の期待値を計算する。まず、

\begin{align}
    \hat{z}_i \ket{\Omega_i} &= \cos{\biggl(\frac{\theta_i}{2}\biggr)}\hat{z}_i \ket{0}_i + e^{\mathrm{i}\phi_i}\sin{\biggl(\frac{\theta_i}{2}\biggr)}\hat{z}_i \ket{1}_i \nonumber \\
    &= \cos{\biggl(\frac{\theta_i}{2}\biggr)}\ket{0}_i + e^{\mathrm{i}\phi_i}\sin{\biggl(\frac{\theta_i}{2}\biggr)(-1)}\ket{1}_i
\end{align}

より、

\begin{align}
    \brakett{\Omega_i }{\hat{z}_i|\Omega_i} &= \cos^2{\biggl(\frac{\theta_i}{2}\biggr)}\brakett{0}{0} - \sin^2{\biggl(\frac{\theta_i}{2}\biggr)}\brakett{1}{1} \nonumber \\
    &= \cos^2{\biggl(\frac{\theta_i}{2}\biggr)} - \sin^2{\biggl(\frac{\theta_i}{2}\biggr)} \nonumber \\
    &= \cos{\theta_i}
\end{align}

となり、(9)と一致する。

上記をまとめると、試行関数・仮説(3)でハミルトニアン(2)の期待値を計算する。
その時、ハミルトニアン(2)のパウリ演算子を変換規則(7),(8),(9)に従って演算子から実数に変換する。
ハミルトニアンは$\bm{\Omega}=(\phi_i \theta_i)^{N_q}_{i=1}$の関数なので、この変数について最小値を求めることになる。

B.2 Multi-Qubit Unitary Transformation

2つ目ののステップでは次のMulti-Qubit Unitary Transformation

\begin{align}
    \hat{U}(\bm{\tau}) = \prod^{N_{\text{ent}}}_{k=1}\exp{(-\mathrm{i}\tau_k \hat{P}_k/2)} \tag{11}
\end{align}

を導入して変文仮設を設計していく。
$\hat{P}_k$は複数の量子ビットのまたがって作用するパウリ演算子であり、エンタングラーと呼ばれている。
QMFのの変分仮説(3)は異なる電子状態間に相互作用がなかったが、(11)ではエンタングラーを導入して相関を持たせるのが目的である。$\tau_k$は上記のユニタリ変換の強度を制御するパラメータで定義域は、

\begin{align}
    \tau_k \in [0, 2\pi) ,\;\;\; (k=1,\dots, N_{\text{ent}}) \tag{12}
\end{align}

である。$\hat{P}_k$の例としては制御ゲート系が該当すると思います。
制御ゲートは主に2量子ビット間に作用し制御ビットが$\ket{1}$の時に標的ビットに特定の演算子を作用させる種類のゲートになる。
例えば制御Xゲートは、

\begin{align}
    \hat{C}_X = \hat{x}_2\ket{1}_1\bra{1}_1 + \hat{I}_2\ket{0}_1\bra{0}_1
\end{align}

と表せられる。実際に$\ket{1}_1\ket{0}_2$に作用させると、

\begin{align}
    \hat{C}_X\ket{1}_1\ket{0}_2 &= \hat{x}_2\brakett{1}{1}_1\ket{0}_2 + \hat{I}_2 \brakett{0}{1}_1 \ket{0}_2 \nonumber \\
    &= \ket{1}_1 (\hat{x}_2 \ket{0}_2) \nonumber \\
    &= \ket{1}_1 \ket{1}_2 \tag{13}
\end{align}

となる。この制御Xゲートをパウリ演算子だけで表現すると

\begin{align}
    \hat{C}_X = \frac{1}{2}\biggl(\hat{I} + \hat{z}_1 + \hat{x}_2 - \hat{z}_1\hat{x}_2 \biggr)
\end{align}

となる。先ほどと同様に$\ket{1}_1\ket{0}_2$に作用させると、

\begin{align}
    \hat{C}_X \ket{1}_1\ket{0}_2 &= \frac{1}{2}\biggl(\hat{I} + \hat{z}_1 + \hat{x}_2 - \hat{z}_1\hat{x}_2 \biggr) \ket{1}_1\ket{0}_2 \nonumber \\
    &= \frac{1}{2}\biggl(\ket{1}_1\ket{0}_2 - \ket{1}_1\ket{0}_2 + \ket{1}_1\ket{1}_2 + \ket{1}_1\ket{1}_2 \biggr) \nonumber \\
    &= \ket{1}_1 \ket{1}_2
\end{align}

となり、(13)と一致する。より詳しい制御ゲートの作り方は制御ゲートの作り方が参考になります。

この$\hat{U}(\bm{\tau})$を$\ket{\bm{\Omega}}$に作用させた状態を作り出して$\hat{H}$の期待値、

\begin{align}
    E_{QCC} := \min_{\bm{\Omega, \bm{\tau}}}  \braket{\bm{\Omega}} {\hat{U}^{\dagger}(\bm{\tau}) \hat{H} \hat{U}(\bm{\tau})}{\bm{\Omega}} \tag{14}
\end{align}

を計算する。
このエネルギーをQCCエネルギーと呼ぶ。ユニタリ変換(11)によりハミルトニアンは、$\hat{U}^{\dagger}(\bm{\tau}) \hat{H} \hat{U}(\bm{\tau})$に変換されたと読み替えることが出来る。
演算子の時間発展を

\begin{align}
    \hat{A}^{(0)} &= \hat{H} \\
    \hat{A}^{(1)} (\tau_1) &= e^{\mathrm{i} \tau_1\hat{P}_1/2} \hat{A}^{(0)} e^{-\mathrm{i} \tau_1\hat{P}_1/2} \\
    \hat{A}^{(2)} (\tau_2, \tau_1) &= e^{\mathrm{i} \tau_2\hat{P}_2/2} \hat{A}^{(1)} (\tau_1) e^{-\mathrm{i} \tau_2\hat{P}_2/2} \\
   \vdots \\
    \hat{A}^{(k)} (\tau_k, \dots \tau_1)  &= e^{\mathrm{i} \tau_k\hat{P}_k/2} \hat{A}^{(k-1)} (\tau_{k-1}, \dots \tau_1) e^{-\mathrm{i} \tau_k\hat{P}_k/2}
\end{align}

と定義する。$k$と$k-1$の関係は

\begin{align}
    \hat{A}^{(k)} (\tau_k, \dots \tau_1)  &= e^{\mathrm{i} \tau_k\hat{P}_k/2} \hat{A}^{(k-1)} (\tau_{k-1}, \dots \tau_1) e^{-\mathrm{i} \tau_k\hat{P}_k/2} \nonumber\\
    &= \hat{A}^{(k-1)} - \mathrm{i}\frac{\sin{\tau_k}}{2}[\hat{A}^{(k-1)}, \hat{P}_k] + \frac{1}{2}(1 - \cos{\tau_k}) \hat{P}_k [\hat{A}^{(k-1)}, \hat{P}_k] \tag{15}
\end{align}

となる。この関係式(15)の導出を行う。まず、$\hat{P}_k$が、

\begin{align}
    \hat{P}_k &= \hat{P}^{\dagger}_k \\
    \hat{P}^2_k &= \hat{I}
\end{align}

を満たすとき、

\begin{align}
    e^{-\mathrm{i} \tau_k\hat{P}_k/2} &= \cos{\frac{\tau_k}{2}}\hat{I} -\mathrm{i} \sin{\frac{\tau_k}{2}} \hat{P}_k \tag{16}
\end{align}

となる。何故なら、

\begin{align}
    e^{-\mathrm{i} \tau_k\hat{P}_k/2} &= \sum^{\infty}_{n=0}\frac{(-\mathrm{i} \tau_k\hat{P}_k/2)^n}{n!} \nonumber \\
    &= \sum^{\infty}_{m=0}\biggl(\frac{(-\mathrm{i} \tau_k\hat{P}_k/2)^{2m}}{2m!} + \frac{(-\mathrm{i} \tau_k\hat{P}_k/2)^{2m+1}}{(2m+1)!} \biggr) \nonumber \\
    &= \sum^{\infty}_{m=0} \frac{(- \tau_k/2)^{2m}}{2m!} (\hat{P}^2_k)^m + (-\mathrm{i}) \sum^{\infty}_{m=0} \frac{(- \tau_k/2)^{2m+1}}{(2m+1)!} (\hat{P}^2_k)^m\hat{P} \nonumber \\
    &= \cos{\frac{\tau_k}{2}}\hat{I} -\mathrm{i} \sin{\frac{\tau_k}{2}} \hat{P}_k
\end{align}

となり、(16)と一致する。(16)を利用すると、

\begin{align}
    e^{\mathrm{i} \tau_k\hat{P}_k/2}\hat{A} e^{-\mathrm{i} \tau_k\hat{P}_k/2} &=  \biggr(\cos{\frac{\tau_k}{2}}\hat{I} + \mathrm{i} \sin{\frac{\tau_k}{2}} \hat{P}_k \biggr)\hat{A}\biggl(\cos{\frac{\tau_k}{2}}\hat{I} -\mathrm{i} \sin{\frac{\tau_k}{2}} \hat{P}_k \biggr) \nonumber \\
    &= \cos^2{\frac{\tau_k}{2}} \hat{A} -\mathrm{i} \sin{\frac{\tau_k}{2}} \cos{\frac{\tau_k}{2}} \hat{A}\hat{P}_k + \sin{\frac{\tau_k}{2}} \cos{\frac{\tau_k}{2}} \hat{P}_k \hat{A} + \sin^2{\frac{\tau_k}{2}} \hat{P}_k \hat{A} \hat{P}_k \nonumber \\
    &= \cos^2{\frac{\tau_k}{2}} \hat{A} - \mathrm{i}\frac{\sin{\tau_k}}{2}[\hat{A}^{(k-1)}, \hat{P}_k] + \sin^2{\frac{\tau_k}{2}} \hat{P}_k\biggr( [\hat{A}, \hat{P}_k] + \hat{P}_k\biggl) \nonumber \\
    &= \hat{A} - \mathrm{i}\frac{\sin{\tau_k}}{2}[\hat{A}^{(k-1)}, \hat{P}_k] + \frac{1}{2}(1 - \cos{\tau_k})\hat{P}_k [\hat{A}, \hat{P}_k] \tag{17}
\end{align}

となる。途中で、$[\hat{A}, \hat{P}] =\hat{A}\hat{P} - \hat{P}\hat{A}$より、$\hat{A}\hat{P} = [\hat{A}, \hat{P}] + \hat{P}\hat{A}$を途中で利用した。
(16)を再帰的に$k$について繰り返すと(15)が得られることが分かる。

\begin{align}
    \hat{A}^{(k)} (\tau_k, \dots \tau_1)  &=  \hat{A}^{(k-1)} - \mathrm{i}\frac{\sin{\tau_k}}{2}[\hat{A}^{(k-1)}, \hat{P}_k] + \frac{1}{2}(1 - \cos{\tau_k}) \hat{P}_k [\hat{A}^{(k-1)}, \hat{P}_k] \nonumber
\end{align}

より、$k=1, \dots,N_{\text{ent}}$に対して、元のハミルトニアンに$3^{N_{\text{ent}}}$個の項が新しく追加されることが分かる。
$N_{\text{ent}}$の数が小さくても良い結果が得られることはすでに確認されているらしい。
エンタングラー$\hat{P}_k$の選び方はこの論文で提案されている。

$U^{\dagger}(\bm{\tau}) \hat{H}U(\bm{\tau})$を上記の関係式を用いて展開し、$\ket{\bm{\Omega}}$で期待値をとると変換規則(7)~(9)

\begin{align}
    \hat{x}_i &\to \sin{\theta_i} \cos{\phi_i} \\ 
    \hat{y}_i &\to \sin{\theta_i} \sin{\phi_i} \\
    \hat{z}_i &\to \cos{\theta_i} 
\end{align}

によりパウリ演算子はスカラー($\theta, \phi$)に変換される。
つまり、$E_{\text{QCC}}$(14)は$\bm{\Omega}=(\phi_i , \theta_i)^{N_q}_{i=1}$と$\bm{\tau} =(\tau_k)^{N_{\text{ent}}}_{k=1}$に依存しており、主に

\begin{align}
    \sin{\phi_i}, \cos{\phi_i}, \sin{\theta_i}, \cos{\theta_i}, \sin{\tau_k}, (1 - \cos{\tau_k}) \tag{18}
\end{align}

の要素から構成されている。
上記の変換では$\hat{x}^2 = \hat{y}^2 = \hat{z}^2 = \hat{I}$に注意すると、(18)の$\phi_i, \theta_i$に依存する項は1次の項までしか$E_{\text{QCC}}$に現れない($\sin^2{\phi_i},\sin^3{\phi_i} $などが現れない)。同様に(15)の変換からも$\tau_k$の要素は1次の項までしか現れない。

C. Domain Reduction by Folding

このセクションでは前のセクションで定義したQMFやQCCのエネルギーを最適化する時に利用するDomain Foldingと呼ばれる手法について説明する。

QMFやQCCのエネルギーは次の変数の1次項までが含まれる線形多項式で表される。

\begin{align}
    \sin{\phi_i}, \cos{\phi_i}, \sin{\theta_i}, \cos{\theta_i}, \sin{\tau_k}, (1 - \cos{\tau_k}) \nonumber
\end{align}

しかし三角関数は$\phi,\theta,\tau$について非線形である。三角関数は定義域で最低1つの極値を持つ。
1変数に関する三角変数であれば楽であるが多数の三角関数が集まると大域的な最小値に到達するのが難しくなる。
例えば$\sin{\phi_1}$の最小値は$\phi_1=3\pi/2$の時$-1$になる。$\sin{\phi_1}\cos{\phi_2}$では、$(\phi_1, \phi_2) = (3\pi/2, 0), (\pi/2, \pi)$の時に最小値$-1$をとる。
このように複数の三角関数がかけ合わさると定義域の中で関数が単調に増加(または減少)しないため最適化が難しくなる。
Domain Foldingでは元々の変数の定義域(4),(5)

\begin{align}
    \phi_i &\in [0, 2\pi) \\
    \theta_i &\in [0, \pi), \;\;\;(i=1,\dots, N_q)
\end{align}

を制限することで三角関数を単調関数に変換する。
この変換に伴って新たなバイナリ変数を追加する必要があり、量子アニーリングではそのバイナリ変数に対するイジングモデルを最適化することになる。

C.1 $\theta$に対するDomain Folding

まずは$\theta$に対するDomain Foldingを行なっていく。
$\theta$の定義域は$\theta \in [0, \pi)$である。
FIG.1(a)の実線の様に、この範囲では$\sin{\theta}$は単調変化な関数ではないが、$\cos{\theta}$は単調減少な関数である。

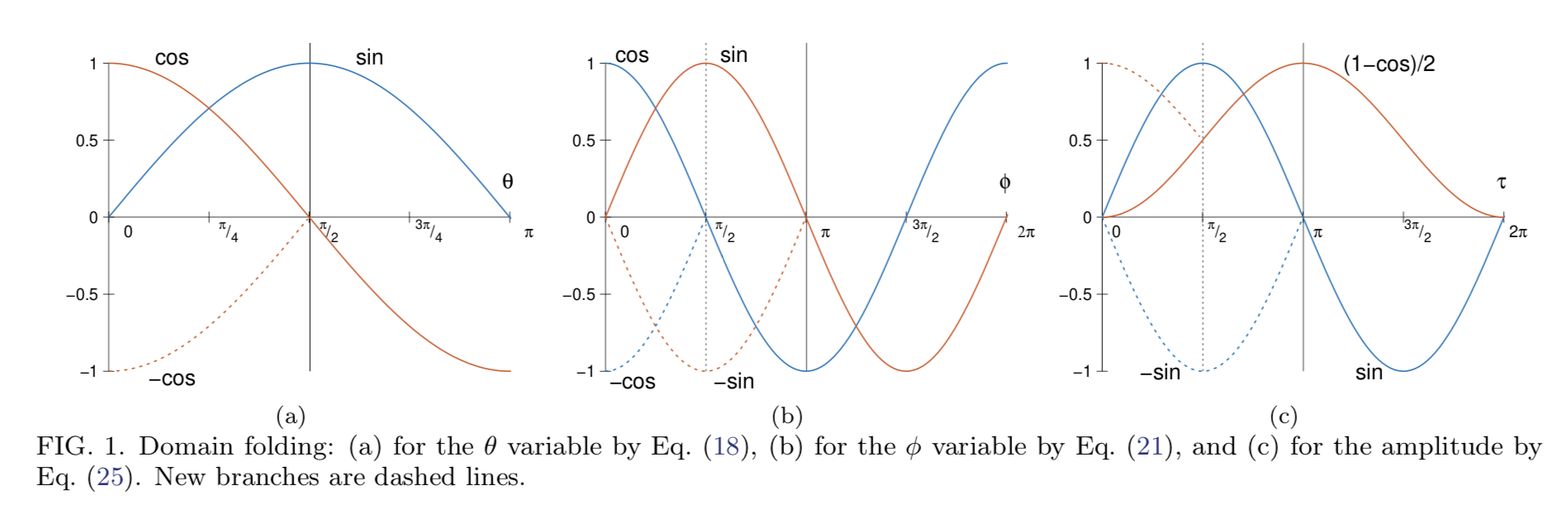
Domain Foldingでは定義域を制限して新たなバイナリ変数を追加することで$\sin{\theta}, \cos{\theta}$の両方を単調関数に変換する。
$\sin{\theta}$は$\theta= \phi/2$に関して対称であり、$\theta \in [0, \pi/2)$では単調増加な関数である。
まず$\theta = \pi/2$に関して折りたたむ(Folding)することを考える。
一方でこの範囲に$\theta$を制限してしまうと$\cos{\theta}$は$\theta= \pi/2$に関して半対称であるので$\theta \in [ \pi/2, \pi)$で取り得る値を失ってしまう。
これを補うために$Z_i \in {\pm 1}$を取るバイナリ変数を導入して、次の変換

\begin{align}
    \sin{\theta_i} &\to  \sin{\theta_i} \\
    \cos{\theta_i} &\to Z_i  \cos{\theta_i} \\
    \theta \in [0, \pi) &\to \theta \in [0, \pi/2), \;\;\; Z_i\in \{\pm 1\} \tag{19}
\end{align}

を施す。
$\cos{\theta}$の$\theta \in [\pi/2, \pi)$の範囲の値を表現するときは$Z_i = -1$とすれば良い。
$Z_i=-1$となった時の$\cos{\theta_i}$の概形はFIG.1(b)の波線で表されている。
元々の$\theta$の定義域(4)から(19)に変換することで、$Z_i$が固定されると$\sin{\theta_i}, \cos{\theta_i}$を単調関数になる。

C.2 $\phi$に対するDomain Folding

$\phi$に対しても同様の変換を施していく。
$\phi$の定義域は$\phi \in [0, 2\pi)$であり、
$\sin{\phi}, \cos{\phi}$の概形はFIG.(b)の実線で表せられる。
この範囲では両方とも単調関数ではない。今回は2段階のFoldingを行う。
まずは$\phi=\pi$でのFoldingを行うと、

\begin{align}
    \sin{\phi_i} &\to  Q_i\sin{\phi_i} \\
    \cos{\phi_i} &\to  \cos{\phi_i} \\
    \phi \in [0, 2\pi) &\to \phi \in [0, \pi)\\
    Q_i  &\in \{\pm 1\}
\end{align}

となる。
新たなバイナリ変数$Q_i$が$\sin{\phi_i}$に追加される。
$\cos{\phi_i}$は単調関数になったが$\sin{\phi_i}$は単調関数ではないので、さらに$\phi=\pi/2$でFoldingを行うと、

\begin{align}
    \sin{\phi_i} &\to  Q_i\sin{\phi_i} \\
    \cos{\phi_i} &\to  W_i\cos{\phi_i} \\
    \phi \in [0, \pi) \to \phi &\in [0, \pi/2) \\
    Q_i, W_i &\in \{\pm 1\} \tag{20}
\end{align}

となる。
$Q_i, W_i$がそれぞれ$-1$の場合のグラフの概形はFIG.(b)の波線で表せられる。

C.3 $\tau$に対するDomain Folding

$\tau$に対しても同様の変換を施していく。
$\tau$の定義域は$\tau \in [0, 2\pi)$であり、
$\sin{\tau}, (1-\cos{\tau})/2$の概形はFIG.(c)の実線で表せられる。
今回も2段階のFoldingを行う。まずは$\tau=\pi$でのFoldingを行うと、

\begin{align}
    \sin{\tau_i} &\to  F_i\sin{\tau_i} \\
    (1-\cos{\tau})/2 &\to  (1-\cos{\tau})/2 \\
    \tau &\in [0, \pi) \\
    F_i &\in \{\pm 1\}
\end{align}

となる。
新たなバイナリ変数$F_i$が$\sin{\tau_i}$に追加される。
$(1-\cos{\tau})/2$は単調関数になったが$\sin{\tau_i}$は単調関数ではないので、さらに$\tau=\pi/2$でFoldingを行うと、

\begin{align}
    \sin{\tau_i} &\to  F_i\sin{\tau_i} \\
    (1-\cos{\tau})/2 &\to  (1-G_i\cos{\tau})/2 \\
    \tau &\in [0, \pi) \\
    F_i, G_i &\in \{\pm 1\} \tag{21}
\end{align}

となる。
$F_i, G_i$がそれぞれ$-1$の場合のグラフの概形はFIG.(c)の波線で表せられる。

C.4 最適化手順

以上よりエネルギー関数に含まれる全ての三角関数を単調関数に変換することが出来た。

\begin{align}
    \text{連続変数} &: \sin{\phi_i}, \cos{\phi_i}, \sin{\theta_i}, \cos{\theta_i}, \sin{\tau_k}, (1 - \cos{\tau_k}) \nonumber \\
    \text{定義域} &: \phi_i, \theta_i,\tau_k \in [0, \pi/2) \nonumber \\
    \text{離散変数} &: Z_i, Q_i, W_i, F_i, G_i \in \{\pm 1\} \nonumber
\end{align}

この変換に伴い上記の様に新たな離散変数${Z_i, Q_i, W_i, F_i, G_i}$が導入された。最適化手順はまず離散変数の値を固定して連続変数に対して最適化する。次に前の手順で最適化された連続変数の値を固定して離散変数について最適化する。この2つの手順を繰り返していく。この最適化手法で利用されるイジングモデルは一般的に

\begin{align}
    \hat{H}^{\text{gen}}_{Is} = \sum_i A_i \hat{z}_i + \sum_{ij} B_{ij} \hat{z}_i \hat{z}_j + \sum_{ijk} C_{ijk} \hat{z}_i \hat{z}_j \hat{z}_k + \cdots \tag{22}
\end{align}

と表すことが出来る。離散変数、連続変数間の対応関係は

\begin{align}
    \hat{z}_i &\leftrightarrow \{Z_i, Q_i, W_i, F_i, G_i\} 
    \{A_i, B_{ij}, C_{ijk}\} &\leftrightarrow \sin{\phi_i}, \cos{\phi_i}, \sin{\theta_i}, \cos{\theta_i}, \sin{\tau_k}, (1 - \cos{\tau_k})
\end{align}

となる。

上記の変換から分かる様に一般的に$\hat{z}_i$に対して3次以上の項が現れる場合がある。
量子アニーリングマシン、イジングマシンを使う場合は2次以下のQUBOとして表現する必要がある。
3次以上の項が発生するのは、ハミルトニアンの形に由来する場合と、QCCに由来する場合の2パターンが考えられる。
ハミルトニアンに関しては元のハミルトニアン(2)から$E_{QMF}$(4)を計算してFoldingを行なった後に3次以上の項が含まれる場合が考えられる。
QCCでは変換(11)を3回以上施してFoldingを行うときに考えられる。
$\tau_k$の数が増えるにつれて$\tau_k$に関する高次項の数は増加してしまう。

D. Solving the generalized Ising Hamiltonians for various foldings

それぞれの三角関数が何回Foldingされたのかを次のノーテーションで表す。

\begin{align}
    (m, n),\;\;\text{where} \; 1\le m \le 3,\; 0\le n \le 2
\end{align}

$n$は$\tau$がFoldingされた回数を表す。$m$は$\theta, \phi$のFoldingされた回数の合計を表すが、次のように$m$の値によって微妙に場合分けされている。

• $m=1$ : $\theta$のみが1回だけFoldingされた
• $m=2$ : $\theta, \phi$が1回ずつFoldingされた
• $m=3$ : $\theta$が1回、$\phi$が2回Foldingされた

これより項の数は$(mN_q+nN_{ent})$となる。

$(m, n)=(3, 2)$で計算が行うのがベストであるが、最適化計算の難易度と必要なビット数の間のトレードオフを考慮する必要がある。$(m, n)$の値が低いと必要なビット数が減りハミルトニアンが簡素化されるのでエネルギー計算は容易になる。
ハミルトニアンの正確性は落ちる。$(m, n$を増加させると必要なビット数は増えより正確にハミルトニアンを表現できるが最適化計算が難しくなる。
Foldingの回数を増やすごとに補助変数$\hat{z}_i$が追加される。三角関数の積の次数が3以上の場合は2次以下にするためにさらに補助変数が必要となる。
使えるビット数に制限があるため全ての項を最大可能回数でFoldingできるとは限らない。
今回の手法と比較を行うために(22)のハミルトニアンを厳密対角化する時の手法を**Ideal Ising Machine(IIM)**と呼ぶことにする。
C$_6$H$_6$はフォック空間の次元が$2^{36}$になるため厳密対角化は出来ないようです。

3. 計算結果

LiHとH$_2$OはQMFとQCCの両方で、C$_6$H$_6$はQMFだけで計算を行っています。
計算結果はFIG.2に載っています。量子アニーリングマシンにはD-Wave 2000Qを使用しています。
D-waveでの計算は全ての分子に対して計算時間は$100\mu[s]$で行われています。
サンプルの個数は全て1000個です。
ブロッホ角度と強度の最適化には{\bf L-BFGS-B}と呼ばれる勾配最適化アルゴリズムを利用しています。
それぞれの分子のハミルトニアンに必要な量子ビット数はFigure.\ref{fig:TABLE}に記載されています。

平衡状態の近くでは$\le 1$kcal;mol$;^{-1}$の精度の結果をQCCでは得られているようです。
平衡状態の計算ではLiとH間の距離$R$を$R=1.54\mathrm{\mathring{A}}$として計算される。
そこから少し離れた$R=3.20\mathrm{\mathring{A}}$でも計算を行っています。
同様にO-H間では対称的にストレッチされた長さである$R=2.05\mathrm{\mathring{A}}$(平衡状態では$R=0.96\mathrm{\mathring{A}}$)、C-C間では対称的に引き伸ばされた$R=1.5914\mathrm{\mathring{A}}$(平衡状態では$R=1.34\mathrm{\mathring{A}}$)でも計算を行っています。

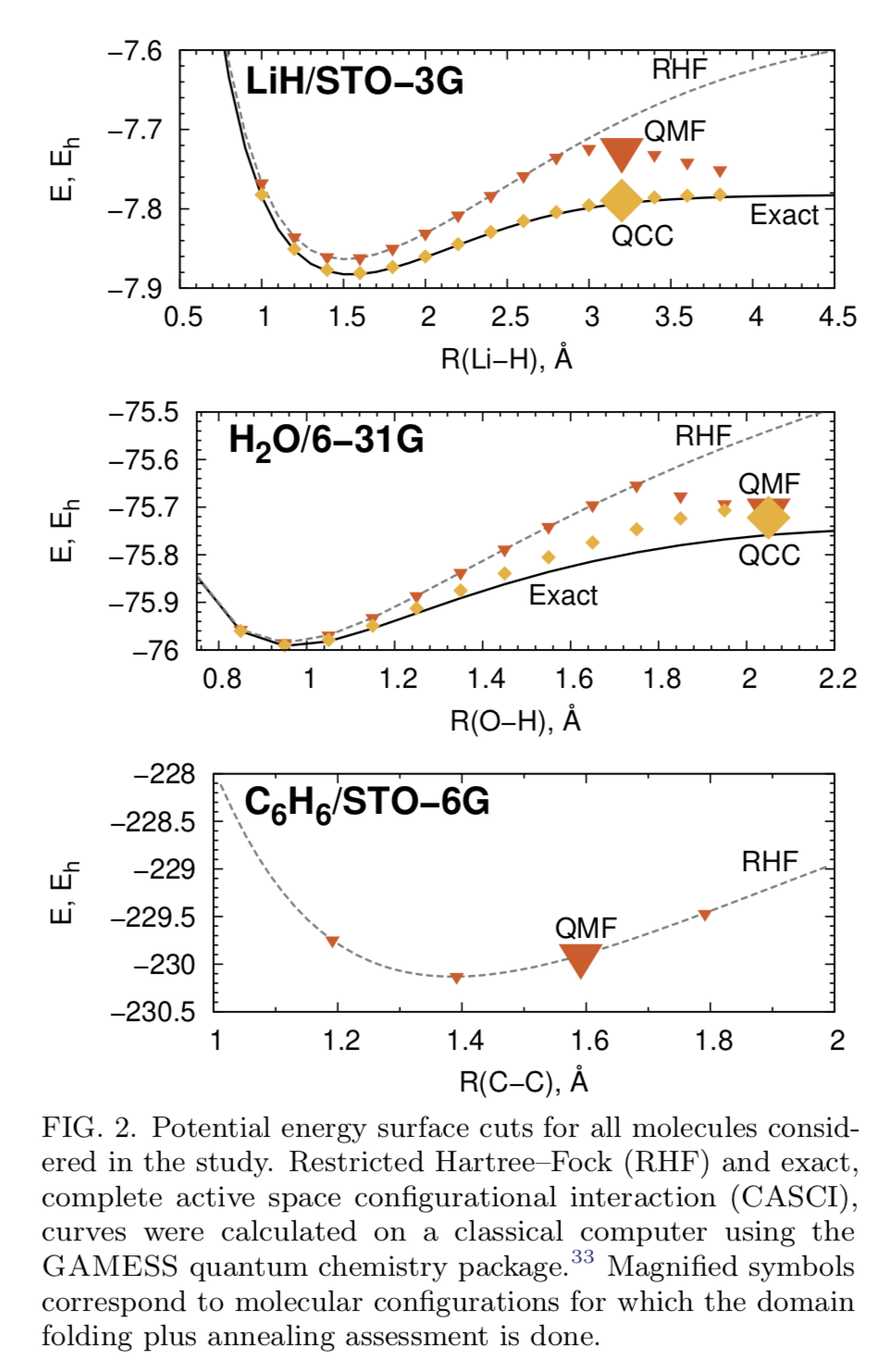
C$_6$H$_6$以外は厳密対角化が行える。
マークが大きくなっている場所が平衡状態から離れた原子間距離を示している。
QMFの結果はRHFとほとんど一致している。QCCの結果はIIMとほとんど一致している。

LiH, H$_2$Oに対してFoldingを行わない場合と比較した計算結果がFIG3, 4にそれぞれ記載されています。

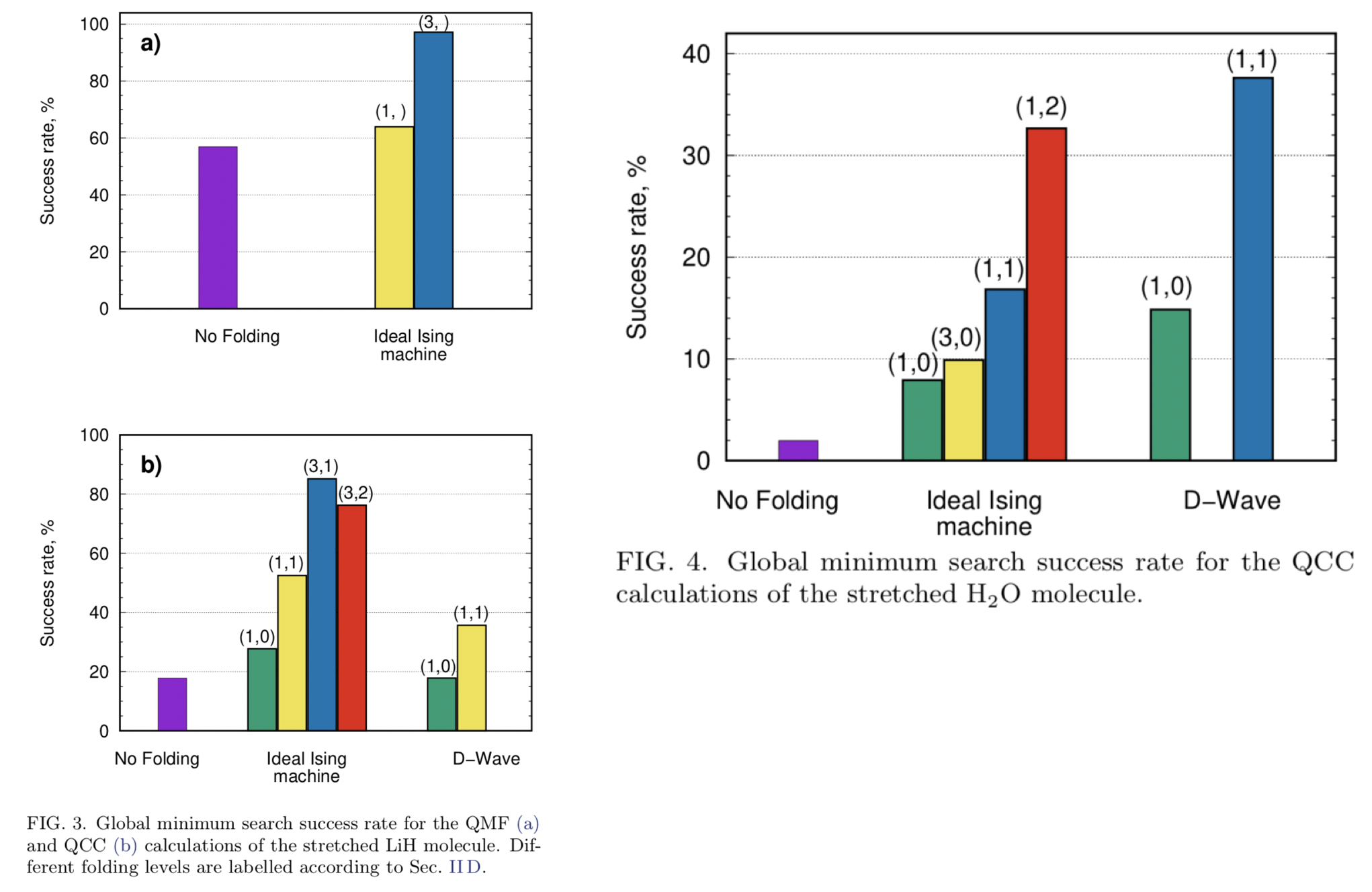
図にはそれぞれの手法で計算を行った場合に最適解に到達した割合が記載されています。
FIG.3(a)にはLiHに対してQMFをFoldingを行わなかった場合と行った場合の計算結果が載っています。
IIMでの結果ですがFoldingを行った方が最適解に到達する割合が増加しています。
FIG.3(b)には同様にQCCの計算結果が記載されています。
こちらもFoldingを行った方が結果は良くなっています。
こちらはD-waveでの計算も行っています。Foldingを行わない場合に比べて若干良くなっています。

FIG.4ではH$_2$OでQCCで計算した時の結果が記載されています。
こちらはD-waveでFoldigを行った場合の結果が最も良くなっています。

C$_6$H$_6$は原子軌道が$36$個でフォック空間が$2^{36}\simeq 6.87\times 10^{10}$になるためIIMでの
計算が行えないため比較結果はありません。

まとめ

Domain FoldingではQMF, QCCに現れていた局所的な対称性(三角関数の?)を利用して大域的な最小値に到達する割合が高まっています。
QMF, QCCは元々ゲート方式で(ユニバーサルな量子コンピュータ)で定式化された手法であるがDomain Foldingを用いれば量子アニーリングでも計算が行える。LiH, H$_2$O,C$_6$H$_6$の分子では今回の手法の有効性が示せたようです。

QMF, QCCでは古典コンピュータでの計算が必要になるが、対称性が破れていたり電子相関の強い系でも量子アニーリングと組み合わせる事で計算が効率的に行えることが期待される。
これらの系では複数の局所解が発生する事が多いので量子アニーリングが役に立つ。
QCCとDomain Foldingを組み合わせた手法は平均場近似を超えて強電子相関系の計算が行えることが期待される。

非常に面白い論文だと思いました(小並感)。
量子系に限らず三角関数の入った最適化問題？でもこのハイブリット解法が使えるんじゃないかと思いました。
どれだけ効率的かはわかりませんが...。
QMFやQCCについて手を動かしながら理解できたので良かったです。