整数計画問題の良い線形緩和について

CouseraのDiscrete Optimization(離散最適化)の授業を受けています。
課題が非常に難しくてなかなか先に進めないのですがようやくweek6が終了しました。
week6の授業で解説されていて「なるほどな！」と思った、整数計画問題と線形緩和問題のギャップについてメモを残しておきます。
MIPソルバーを使う上で良い定式化とは何なのかが少し分かります。
(数理最適化のプロからすれば当たり前かと思われる内容かもしれません。)
(そして私は数理最適化のプロではないのでこの記事に誤った内容が記載されている場合もあります。)

上界と下界について

整数計画問題の基本型は

\begin{align}
\min_{x}\;\;\;& \sum^n_{j=1}c_jx_j \\
s.t. \;\;\;& \sum^n_{j=1}a_{ij}x_j \ge b_i \;\;\; (i=1,\dots,m)\\
&x_j \in Z_{+} \;\;\; (\text{0を含む正の整数の集合})
\end{align}

と表すことができます。
この問題をMIPソルバー(Pulp, CPLEX, Gurobiなど)で解く場合、内部では元の問題の条件を緩和した問題(緩和問題)を解いて探索する変数の範囲を制限したり、得られた解が厳密解(最適解)であるかどうかを判定しています。
条件を緩和しているので緩和問題は元の問題よりも良い値(低い値、見積もりが甘い値)を解として出力します。
(もちろん整数値でなく実数値の場合があるので元の問題の解にはなり得ません。)

今、$x_j$は整数ですがこれを連続値に緩和した問題(線形緩和問題)であれば比較的楽に解けます。
この線形緩和問題を解いて得られた解の値は常に元の問題の最小値以下になります。
つまり線形緩和問題の解は元の問題の下界を与えてくれます。
元の問題で現在得られているベスト解が上界になり、上界と下界がぴったり一致すると厳密解(最適解)であると判定されるようです。
この上界とか下界の差のことをギャップと呼びます。

このあたりの関係を視覚的に分かりやすく説明してくれているスライドが以下にあります：

組合せ最適化入門：線形計画から整数計画まで(梅谷 俊治先生)
(上記スライドのp52を参照して下さい。)

MIPソルバーの内部ではp53で説明されている「分枝限定法」が利用されています。
緩和問題を解いて得られた変数の中で整数値でない変数$x_t$を選び、その値を$\bar{x_t}$とします。
$x_t$の探索領域を$x_t\le \lfloor \bar{x_t} \rfloor$と、$x_t\ge \lceil \bar{x_t} \rceil$に分割して再び問題を解いていきます。

$x_t\le \lfloor \bar{x_t} \rfloor$の領域で緩和問題を解いた時にその下界が現在の上界よりも高い場合は、この領域ではどう頑張っても現在のベスト解よりも良い値にならないので探索を終了します。
つまり$x_t\le \lfloor \bar{x_t} \rfloor$には厳密解がないことが判明しました。
($x_t\ge \lceil \bar{x_t} \rceil$だけを気兼ねなく探索すれば良い。)

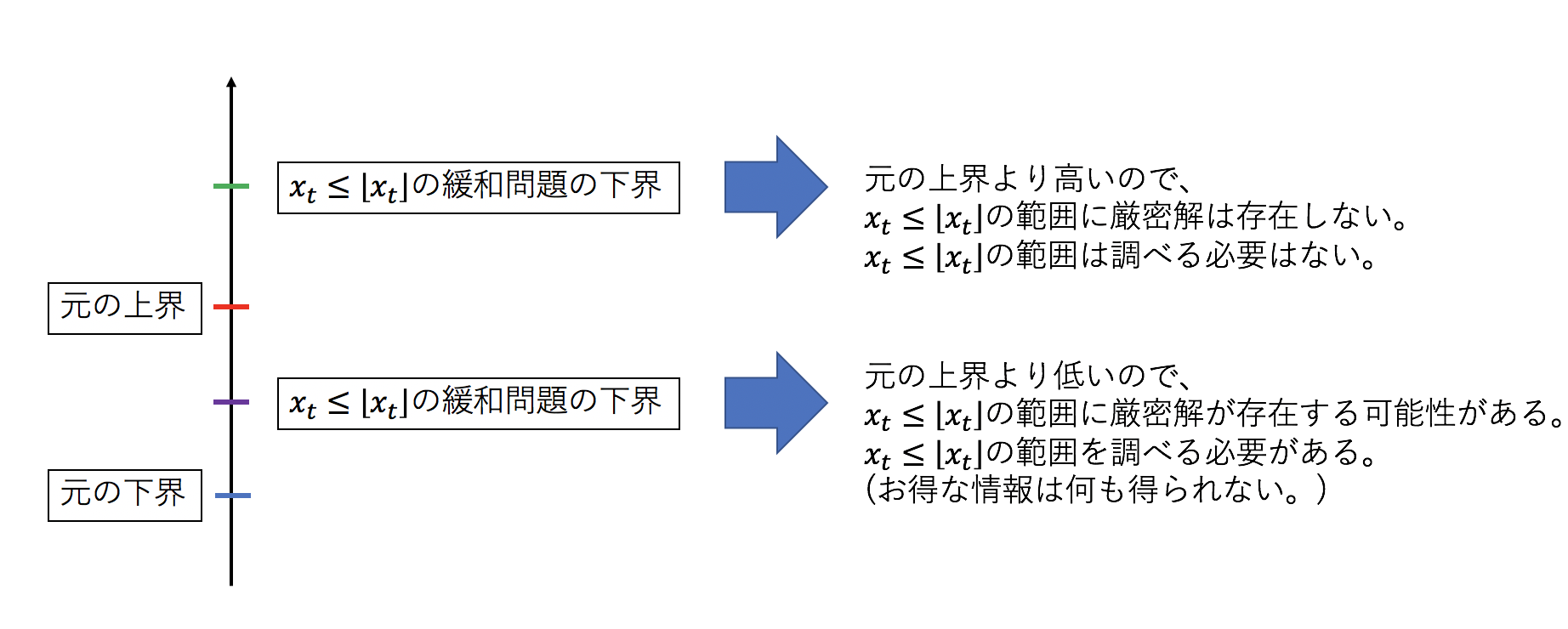
一方で$x_t\le \lfloor \bar{x_t} \rfloor$の領域の下界が元の問題の上界と下界の間にある時は何の情報も得られません。
$x_t\le \lfloor \bar{x_t} \rfloor$の領域に厳密解が存在する可能性があるので、$x_t\le \lfloor \bar{x_t} \rfloor$での探索を続ける必要があります。

これを注目する変数を繰り返しながら行います。
良い定式化を行なった場合は図の緑の位置まで変数をある範囲に制限した問題の下界が上昇してくれます。
一方で悪い定式化を行なった場合は図の紫の位置まで下界が下降します。
定式化の良し悪しにより緩和問題の下界の位置が変動します。

上界と下界のギャップが大きいと変数の範囲を制限して緩和問題を解いても、その結果がギャップの範囲に入ると何も有益な情報が得られません。
このように下界はできるだけ高い方が良く、上界はできるだけ低い方がギャップが小さくなるので良いことが分かります。
MIPソルバーに投げるモデルの定式化を工夫することで下界をより高く引き上げることができます。
逆に悪い定式化だと下界を低く見積もってしまい計算時間が長くなってしまいます。

倉庫配置問題

講義の中で取り上げられていたのが倉庫配置問題(Warehouse Location Problem, Uncapacitated facility Location Problem?)になります。

顧客をどの倉庫に割り当てるかを決める問題で、倉庫をオープンさせるコストとオープンさせた倉庫と顧客との間の距離を最小化する問題です。

変数は倉庫$w$をオープンさせるかどうかを決める変数$x_w$と、顧客$c$が倉庫$w$に割り当てるかどうかを決める変数$y_{w, c}$になります。
係数は倉庫$w$をオープンさせた時のコスト$c_w$と、倉庫$w$と顧客$c$との距離$t_{w, c}$になります。

制約条件は

1. 顧客はオープンした倉庫にしか割り当ててはいけない。
2. 顧客はどこか1つの倉庫にしか割り当ててはいけない。

になります。
(実際の講義の課題ではこの制約に加えて倉庫のキャパシティ制約が加わります。)
これらを定式化すると、次のモデルが得られます。

モデル1

\begin{align}
\min_{x,y}\;\;\;& \sum_{w\in W}c_wx_w + \sum_{w\in W, c\in C}t_{w,c}y_{w,c} \\
s.t. \;\;\;& y_{w, c} \le x_{w} \;\;\; (w\in W, c\in C) \\
& \sum_{w\in W}y_{w, c} = 1 \;\;\; (c\in C) \\
& x_w \in \{0, 1\} \;\;\; (w\in W) \\
& y_{w, c} \in \{0, 1\} \;\;\; (c\in C)
\end{align}

また別の定式化として制約条件1

y_{w, c} \le x_{w} \;\;\; (w\in W, c\in C)

を少し変形して、顧客$c$に関して和をとって、

\sum_{c\in C}y_{w, c} \le |C|x_{w} \;\;\; (w\in W)

としたモデル2を考えます。

モデル2

\begin{align}
\min_{x,y}\;\;\;& \sum_{w\in W}c_wx_w + \sum_{w\in W, c\in C}t_{w,c}y_{w,c} \\
s.t. \;\;\;& \sum_{c\in C}y_{w, c} \le |C|x_{w} \;\;\; (w\in W) \\
& \sum_{w\in W}y_{w, c} = 1 \;\;\; (c\in C) \\
& x_w \in \{0, 1\} \;\;\; (w\in W) \\
& y_{w, c} \in \{0, 1\} \;\;\; (c\in C)
\end{align}

数値計算

上記2つのモデルをMIPソルバーで解いた時の下界の精度について調べます。
データセットはweek6の課題に含まれている物を使用しました。
以下のページにあるdataフォルダを参照して下さい。

コードは上記にあるsolver_test.pyを使用しました。
PULPを使って実装しています。
PULPは計算時間の上限を60秒に設定しています。
後はログを出力するフラグを立てているだけでそれ以外はデフォルト設定です。

倉庫数が増えすぎるとPULPだと解けなくなるので倉庫数が200個までのデータセットで計算をしました。

結果は以下のようになりました。

データセット	倉庫数	顧客数	モデル1(下界)	モデル2(下界)	%(下界)	モデル1(計算時間[s])	モデル2(計算時間[s])
fl_50_1	50	50	2.76543e+06	2.72751e+06	1.4	0.1	0.18
fl_50_5	50	100	1.12678e+06	784725	30.4	0.36	0.58
fl_50_6	50	200	3.72316e+06	3.3984e+06	8.7	1.09	0.8
fl_100_7	100	100	1965.55	1743.85	11.3	0.81	34.06
fl_100_11	100	500	7.10975e+06	5.37458e+06	24.4	3.31	6.33
fl_100_14	100	800	5.07341e+06	4.09975e+06	19.2	14.26	12.17
fl_200_1	200	200	3807.32	3421.99	10.1	9.55	60*
fl_200_2	200	200	3964.14	3664.48	7.6	10.6	60*
fl_200_6	200	400	2.578e+06	1.51211e+06	41.3	4.63	13.57
fl_200_7	200	800	4.57142e+06	3.13896e+06	31.3	20.21	29.64

(*は60秒間で厳密解に到達しなかったケース。)
%には(下界1- 下界2)/下界1の割合を表記しています。

どのデータセットを見てもモデル1の方が下界が高くなっています。
またデータセットfl_100_14を除いて厳密解に到達した時の計算時間もモデル1の方が早くなっています。
(fl_100_14もその差は2秒ほどしかない。)
下界の質が良いと計算時間も短くなることが分かります。

モデル1の不安要素

モデル1の不安要素を無理やり挙げるとすれば実装時に倉庫$w$と顧客$c$の変数に対してループを回す必要がある点です。
私はPulpしか使用したことがないのですが、以下のコードの様に愚直に+=で不等式を追加するしかない場合はモデルの生成に結構時間がかかってしまいます。

for i in range(warehouse_num):
    for j in range(customer_num):
        model += y_wc[i, j] <= x_w[i]

今回計算したデータセットの規模であれば一瞬なのですが。
一方でモデル2ではPulpの中のpulp.lpSumを使用できるためモデル1に比べてモデルの生成時間自体は若干早く済みます。
(参考ページ：python pulp 変数和(サブロウ丸さん))

for i in range(warehouse_num):
    model += pulp.lpSum([y_wc[i, j] for j in range(customer_num)]) <= customer_num * x_w[i]

まぁこの辺りは使用するソルバーごとに違うのでそれほどデメリットにはならないと思います。
モデル2の実装も結局変数が多くなるとモデル生成に時間がかかってしまいます。
CPLEXやGurobiなどの商用ソルバーは使ったことはないですが、きっとこの辺りの実装面の最適化も行われているのでしょう。

原因

モデル1とモデル2で下界の精度が異なる原因は何なのでしょうか？
講義で説明されていたのは、それぞれのモデルの緩和解に対して制約条件1の不等式の包含関係を調べることで下界の精度を判定できるという説明でした。

具体的に説明します。
まず、モデル1の緩和問題の解は制約条件1

y_{w, c} \le x_{w} \;\;\; (w\in W, c\in C)

を当然満たします。一方でモデル2の制約条件1

\sum_{c\in C}y_{w, c} \le |C|x_{w} \;\;\; (w\in W)

も必ず満たします。(単純に顧客について和をとるだけなので。)
つまりモデル1の緩和解は必ずモデル2の緩和解に含まれます。

一方でモデル2の緩和問題の解はモデル2の制約条件1

\sum_{c\in C}y_{w, c} \le |C|x_{w} \;\;\; (w\in W)

は当然満たしますが、モデル1の制約条件1を必ず満たすとは限りません。
モデル1の方が解の範囲を絞れていることが分かります。

例えば$|C|=4, x_w=0.5$で、$y_{w,1}=1, y_{w,2}=1, y_{w,3}=0, y_{w,4}=0$の場合、モデル2の制約条件1は満たされます。
一方でこの時、$y_{w,3}, y_{w,4}$はモデル1の制約条件1を満たしますが、$y_{w,1}, y_{w,2}$は満たしません。
モデル2の緩和問題の解の一部はモデル1から見ると実行不可能な領域を探索してしまっています。
一方でモデル1の緩和問題の解は必ずモデル2の実行可能領域に所属しています。

モデル2の制約条件1ではある倉庫$w$に対応する$y_{w,c}$が$C$全体で右辺の$|C|$を超えない範囲で変化することが出来ます。
これによりモデル1に比べて$y_{w,c}$が取り得る値のバリエーションは増えて、その中に目的関数の値を下げる値の組合せがあれば下界を下げることが出来ます。

(図はイメージです。)

モデル2の制約条件1のようにそれぞれの制約条件をまとめて1つにすると数式的にはコンパクトにシンプルに見えますがその問題を緩和した時に余計な領域を探索する確率が高くなってしまいます。
不等式の右辺に比較的大きな数$|C|$が入ることで$y_{w, c}$が動くことのできる領域が増えるためだと考えられます。
(大きな値の定数(Big M)が不等式に入ると途端にMIPソルバーの精度が悪くなるのも上記のようなことが原因かと思われます。)
一方で不等式の数自体は多くなりますがモデル1の制約条件1だと変数1つ1つにをより細かく制限することができるためより良い下界を得ることができると考えられます。

下界を下げ過ぎてしまうと分枝限定法の精度が悪くなったり、厳密解の判定に時間がかかってしまうため計算時間が長くなってしまいます。
この事はモデル1とモデル2の計算時間を比較した表からも確認できます。

まとめ

定式化を行う時の制約条件は1つの式にまとめ過ぎると下界の精度が悪くなる可能性がある。
(下界を下げ過ぎてしまう。)
複数の制約条件に分離できる場合は分離した方が良い。
不等式の右辺に大きな値があっても同様の現象が起きる。
何らかの前処理でこの値の範囲を制限できれば計算時間の短縮に繋がる。

以上が私の学びのメモでした。

おまけ

ちなみにモデル1とモデル2の制約条件1を両方に取り入れたモデル3でも数値計算を行いました。

モデル3

\begin{align}
\min_{x,y}\;\;\;& \sum_{w\in W}c_wx_w + \sum_{w\in W, c\in C}t_{w,c}y_{w,c} \\
s.t. \;\;\;& y_{w, c} \le x_{w} \;\;\; (w\in W, c\in C) \\
& \sum_{c\in C}y_{w, c} \le |C|x_{w} \;\;\; (w\in W) \\
& \sum_{w\in W}y_{w, c} = 1 \;\;\; (c\in C) \\
& x_w \in \{0, 1\} \;\;\; (w\in W) \\
& y_{w, c} \in \{0, 1\} \;\;\; (c\in C)
\end{align}

計算結果は以下のようになります。

データセット	倉庫数	顧客数	モデル3(下界)	モデル3(計算時間[s])
fl_50_1	50	50	2.76543e+06	0.24
fl_50_5	50	100	1.12678e+06	0.57
fl_50_6	50	200	3.72316e+06	1.32
fl_100_7	100	100	1965.55	1.97
fl_100_11	100	500	7.10975e+06	7.41
fl_100_14	100	800	5.07341e+06	12.58
fl_200_1	200	200	3807.32	17.78
fl_200_2	200	200	3964.14	18.51
fl_200_6	200	400	2.578e+06	12.24
fl_200_7	200	800	4.57142e+06	43.19

下界はモデル1と同じになりましたが、計算時間がモデル1に比べてfl_100_14以外は遅くなっています。

制約式を取捨選択して分離するのが面倒な場合はとりあえず全て入れたモデルで一度計算して見るのが良いのかもしれません。
そこから速度をさらに向上させたい場合はもう一度式と睨めっこして無駄な箇所を省く処理を施す必要があります。