1.はじめに
量子コンピューター Advent Calendar 2020に向けて論文の紹介(レビュー)を行いたいと思います。
普段はイジングマシンに関する研究開発やコンサルティングサービスの提供を行なっています。
業務の中で量子アニーリングを用いてベイジアンネットワークの構造最適化を行なっている以下の論文を読んだのでその内容を紹介したいと思います。
- 題名:Bayesian Network Structure Learning Using Quantum Annealing
量子アニーリングマシンやイジングマシンで計算を行うには最適化したい問題をQUBO(Quadratic Unconstrained Binary Optimization)として表現する必要があります。
上記の論文ではベイジアンネットワークの構造最適化を行うためのQUBOの定式化が提案されています。
QUBOの定式化を説明する前にまずはベイジアンネットワークの基礎事項について説明したいと思います。
(定式化についての説明がメインで実装に関してはこの記事で触れていません。)
Overleafにも同じ内容でまとめているのでこちらを参照して頂いても構いません。
https://ja.overleaf.com/read/rmcrpnnjctrv
※間違いなどがあれば遠慮なくご指摘お願いします。
2.ベイジアンネットワーク
ベイジアンネットワークの用途としては以下の2種類に分類できると思います。
- ベイジアンネットワークの構造を利用して確率を計算する。
- ベイジアンネットワークの構造を観測データから学習する。
1を行うために2が必要になります。
今回の記事では2のベイジアンネットワークの構造を量子アニーリングで計算するためのQUBOの定式化について説明します。
まずはなぜベイジアンネットワークを考えるのか、どういった利点があるのかを説明した後に構造を最適化するための計算手段について順番に説明していきます。
ベイジアンネットワークの利点
ベイジアンネットワークは多変数の同時確率分布を計算する時に役立ちます。
なぜ役立つかというと確率変数間の(非)条件付き独立性が有向グラフとして与えられるからです。
グラフのノードが確率変数、エッジが変数間の因果関係(依存関係)に対応しています。
ノード間にエッジが存在しない場合は対応する確率変数同士が独立であることを意味しています。
ノード$x,y$にエッジが存在しない場合は
\begin{align}
f(x, y) = f(x)f(y)
\end{align}
となります。
多変数の同時確率分布は事後確率を計算するときに必要になります。
例えば、3変数$x,y,z$に関して事後確率$f(y,z|x)$を求めたい場合、ベイズの定理より
\begin{align}
f(y, z|x) = \frac{f(x|y,z)f(y,z)}{f(x)}
\end{align}
条件付き確率$f(x|y,z)$と$y,z$の事前分布f(y,z)が与えられているとして、分母の$f(x)$を計算する必要があります。
これは$f(x,y,z)$を$y,z$に対して周辺化することで求められます。
\begin{align}
f(x) = \sum_{y,z} f(x,y,z) = \sum_{y,z} f(x|y,z)f(y,z)
\end{align}
$f(x,y,z)$に含まれる変数間の依存関係がベイジアンネットワークに図示されており、その情報を参照することで上記の周辺化が効率的に行える場合があります。
以下では具体的にそのメリットについて説明していきます。
あるノードに$x_i$に注目します。
このノードに向かってエッジをだしている側を親、エッジが向かっているノードを子と呼びます。
$x_i$の親のノードの集合を$\Pi(x_i)$と定義すると同時確率分布は
\begin{align}
f(\boldsymbol{x}) = \prod_i f(x_i|\Pi(x_i))
\end{align}
と表すことが出来ます。
$\Pi(x_i)=\emptyset$の場合は$f(x_i|\Pi(x_i))=f(x_i)$と定義されます。
ベイジアンネットワークには$\Pi(x_i)$が図示されています。
これを参照することで同時確率分布の計算が効率的に行えます。
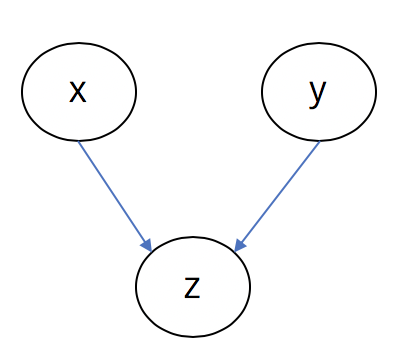
例えば、上図のようなベイジアンネットワークについて考えます。
エッジが$x\to z, y\to z$についているので、
\begin{align}
\Pi(x) &= \emptyset\\
\Pi(y) &= \emptyset\\
\Pi(z) &= \{x, y\}\
\end{align}
である事が分かります。
これより同時確率分布は
\begin{align}
f(x, y, z) = f(x|\Pi(x))f(y|\Pi(y))f(z|\Pi(z)) = f(x)f(y)f(z|x,y)
\end{align}
と表す事ができます。
以下の図のように変数の数を増やして考えてみます。

このベイジアンネットワークが与えられていない場合、形式的には次の形までベイズの定理を使って展開することが出来ます。
\begin{align}
f(w, x, y, z) &= f(w)f(x,y,z|w)\\
& = f(w)f(x|w)f(y,z|w,x)\\
&= f(w)f(x|w)f(y|w,x)f(z|w,x,y)
\end{align}
各変数が2値変数の場合、計算量は248*16=1024になります。
一方で上図のベイジアンネットワークが与えられている場合は、
\begin{align}
f(w, x, y, z) &= f(w)f(x|w)f(y|w)f(z|x,y)
\end{align}
この時の計算量は244*8=256になり計算量は4倍減っている事が分かります。
このようにベイジアンネットワークに図示された確率変数間の条件付き独立を利用する事で同時確率分布の計算が効率的に行える事が分かります。
ベイジアンネットワークは有向グラフであればどんなグラフでも良いわけではなく、**有向非巡回グラフ(DAG:Directed Acyclic Graph)**である必要があります。
DAGとは有向エッジを辿っていく中で巡回するループが存在しないグラフです。
例えば$z\to y\to x\to z$というループが存在していると、
\begin{align}
f(z|x)f(x|y)f(y|z)
\end{align}
となり、$z$に関する条件付き確率を計算する際に矛盾が生じます。
故にベイジアンネットワークはDAGである必要があります。
この条件は後でQUBOに制約条件として反映されます。
以上がベイジアンネットワークを利用する利点の簡単な説明になります。
ベイジアンネットワークが与えられると効率的に同時確率分布が計算できるという話でした。
より詳しい話は以下の資料を参照して下さい。
- ベイジアンネットワーク入門 (須鎗 弘樹)
ベイジアンネットワークの構造学習
観測したデータからベイジアンネットワークを構築(学習)していく方法を以下のpdfを参考にしながら説明していきます。
- 情報意味論 (9) ベイジアンネットワーク(櫻井 彰人)
この構造学習ではある構造を決めるとスコアが求まり、このスコアを最大化するような構造を決定していきます。
構造$m_1,m_2$を考える場合、両方のスコアを計算してスコアの高い方の構造を採用します。
具体的にはデータが与えられた後の構造の事後確率をスコアとして採用します。
データの集合を$D$、構造を$m$で表記すると
\begin{align}
P(m|D) = \frac{P(D|m)P(m)}{P(D)}
\end{align}
を最大化するような$m$を求めていきます。
$P(m)$が一様分布と仮定すると、
\begin{align}
P(m|D) \propto P(D|m)
\end{align}
になります。$P(D|m)$は構造$m$に対応した連続的なパラメータ$\theta_m$を用いて
\begin{align}
P(D|m) = \int P(D|\theta_m, m)P(\theta_m|m)d\theta_m
\end{align}
とパラメトライズすると、Cooper and Herskovits(1992)より以下の式を得ることが出来ます。
\begin{align}
P(D|m) = \prod^{n}_{i=1}\prod^{q_i}_{j=1} \frac{\Gamma(\alpha_{ij})}{\Gamma(\alpha_{ij}+N_{ij})}\prod^{r_i}_{k=1}\frac{\Gamma(\alpha_{ijk}+N_{ijk})}{\Gamma(\alpha_{ijk})}
\end{align}
- $n$: 全ノード数
- $q_i$: ノード$X_i$の親ノードの値の組み合わせ総数
- $r_i$: ノード$X_i$(離散確率変数)のあたいの総数
- $N_{ijk}$: $x_i$の親のあたいの組む合わせが$j$,$x_i$の値が$k$のデータ数
- $\alpha$: 事前分布であるDirichlet分布のパラメータ($i$はノード、$1\ge j\ge q_i$)
また、$N_{ij}=\sum_k N_{ijk},\alpha_{ij}=\sum_k \alpha_{ijk}$になっています。
$N_{ijk}$はどちらかというと「$x_i$の値が$k$で、$x_i$の親のデータの値の組合せが$j$である場合のデータ数」と読み替えたほうが分かりやすいかもしれません。
具体的なデータを使ってスコアを計算していきます。
| データID | X | Y |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 2 |
| 3 | 1 | 1 |
| 4 | 2 | 2 |
| 5 | 1 | 1 |
| 6 | 2 | 1 |
| 7 | 1 | 1 |
| 8 | 2 | 2 |

ネットワークの構造として上図の$m_1,m_2$を仮定してそれぞれのスコアを計算していきます。
まずは$m_1$のスコアから計算していきます。
ノード数は$n=2$で$i=1$を$X$、$i=2$を$Y$に対応させます。
まずは子である$Y(i=2)$に注目していきます。
次に求める必要があるのが$q_2, r_2$になります。
\begin{align}
\prod^{q_i}_{j=1} \frac{\Gamma(\alpha_{2j})}{\Gamma(\alpha_{2j}+N_{2j})}\prod^{r_2}_{k=1}\frac{\Gamma(\alpha_{2jk}+N_{2jk})}{\Gamma(\alpha_{2jk})}
\end{align}
$q_2$は$Y$の親ノードである$X$が取る値の組み合わせになるので2パターン存在します。
$j=1$が$X=1$、$j=2$が$X=2$の状態を表すことにします。
まずは$j=1$に注目すると、
\begin{align}
\frac{\Gamma(\alpha_{21})}{\Gamma(\alpha_{21}+N_{21})}\prod^{r_2}_{k=1}\frac{\Gamma(\alpha_{21k}+N_{21k})}{\Gamma(\alpha_{21k})}
\end{align}
$r_2$は$Y$が取る値の組み合わせなので2パターン存在します。
$k=1$が$Y=1$, $k=2$が$Y=2$を表すことにします。
\begin{align}
\frac{\Gamma(\alpha_{21})}{\Gamma(\alpha_{21}+N_{21})}\frac{\Gamma(\alpha_{211}+N_{211})}{\Gamma(\alpha_{211})}\frac{\Gamma(\alpha_{212}+N_{212})}{\Gamma(\alpha_{212})}
\end{align}
$\alpha$はDirichlet分布のハイパーパラメータなので後で議論することにして、まずは$N_{ijk}$をそれぞれ求めていきます。これはデータから値が求まります。
$N_{ijk}$は「$x_i$の値が$k$で、$x_i$の親のデータの値の組合せが$j$である場合のデータ数」でした。
$N_{211}$は「$Y$の値が1で$Y$の親$X$の値が1であるデータの個数」なので$N_{211}=4$になります。
$N_{212}$は「$Y$の値が2で$Y$の親$X$の値が1であるデータの個数」なので$N_{212}=1$になります。
また、$N_{21}=N_{211}+N_{212}=4+1=5$になります。
続いて$\alpha$の値を決めていきます。
R.E. Neapolitan, Learning Bayesian Networks (2004)によると、
\alpha_{ijk} = \frac{N^{\prime}}{r_i\cdot q_i}
で決めているようです。
$N^{\prime}$はEquivalent Sample Sizeを表しているようです。
今回はおそらく$N^{\prime}=4$になります。(異なるデータのパターン数?)
これより、$\alpha_{211}=\alpha_{212}=1$になります。
また、$\alpha_{21}=\alpha_{211}+\alpha_{212}=2$になります。
以上より$j=1$の場合は、
\begin{align}
&\frac{\Gamma(\alpha_{21})}{\Gamma(\alpha_{21}+N_{21})}\frac{\Gamma(\alpha_{211}+N_{211})}{\Gamma(\alpha_{211})}\frac{\Gamma(\alpha_{212}+N_{212})}{\Gamma(\alpha_{212})} \\
&= \frac{\Gamma(2)}{\Gamma(2+5)}\frac{\Gamma(1+4)}{\Gamma(1)}\frac{\Gamma(1+1)}{\Gamma(1)}
\end{align}
と計算する事が出来ます。
同様に$Y$の$j=2$についても計算します。
($X$が2を取るときのパターン数に対応する量を計算していく。)
$N_{221},N_{222}$を求める必要があります。
これらは$N_{221}=1, N_{222}=2$になります。
これより$N_{22}=3$である事が分かります。
$\alpha$に関しては先ほどと同じ値になります。
よって$j=2$の場合は、
\begin{align}
&\frac{\Gamma(\alpha_{22})}{\Gamma(\alpha_{22}+N_{22})}\frac{\Gamma(\alpha_{221}+N_{221})}{\Gamma(\alpha_{221})}\frac{\Gamma(\alpha_{222}+N_{222})}{\Gamma(\alpha_{222})} \\
&= \frac{\Gamma(2)}{\Gamma(2+3)}\frac{\Gamma(1+1)}{\Gamma(1)}\frac{\Gamma(1+2)}{\Gamma(1)}
\end{align}
以上より$Y$に関する項の計算が終わりました。
続いて$i=1$の$X$について計算を行います。
$X$は親が存在しないので$q_1=1$になります。
よって$j=1$のみを考えます。
\begin{align}
\frac{\Gamma(\alpha_{11})}{\Gamma(\alpha_{11}+N_{11})}\prod^{r_1}_{k=1}\frac{\Gamma(\alpha_{11k}+N_{11k})}{\Gamma(\alpha_{11k})}
\end{align}
$q_i=1$の場合は親が存在しないので自分自身に注目してそれぞれの量を計算していきます。(親が空集合$\emptyset$だと読み替えれば分かりやすいです。)
$r_1$は$X=1,2$を取ることから2パターン存在します。
$k=1$を$X=1$, $k=2$を$X=2$に対応させます。
$N_{ijk}$を計算していくのですが$q_i=1$の場合は少し注意点が必要です。
以前は、
$N_{211}$は「$Y$の値が1で$Y$の親$X$の値が1であるデータの個数」なので$N_{211}=4$になります。
と計算していたのですが、そこを
$N_{111}$は「$X$の値が1で($X$の親$\emptyset$で)あるデータの個数」なので$N_{111}=5$になります。
同様にして、$N_{112}$は「$X$の値が2で($X$の親$\emptyset$で)あるデータの個数」なので$N_{112}=3$になります。
これより、$N_{11}=8$になります。
$\alpha$は$q_1=1$なので$\alpha_{111}=\alpha_{112}=2, \alpha_{11}=4$になります。
以上より、$X$に関しては
\begin{align}
&\frac{\Gamma(\alpha_{11})}{\Gamma(\alpha_{11}+N_{11})}\frac{\Gamma(\alpha_{111}+N_{111})}{\Gamma(\alpha_{111})}\frac{\Gamma(\alpha_{112}+N_{112})}{\Gamma(\alpha_{112})}\\
&= \frac{\Gamma(2)}{\Gamma(2+8)}\frac{\Gamma(2+5)}{\Gamma(2)}\frac{\Gamma(2+3)}{\Gamma(2)}
\end{align}
となります。
長々と計算しましたが以上をまとめると、
\begin{align}
P(D|m_1) & = \prod^{n}_{i=1}\prod^{q_i}_{j=1} \frac{\Gamma(\alpha_{ij})}{\Gamma(\alpha_{ij}+N_{ij})}\prod^{r_i}_{k=1}\frac{\Gamma(\alpha_{ijk}+N_{ijk})}{\Gamma(\alpha_{ijk})}\\
&= \biggl(\frac{\Gamma(2)}{\Gamma(2+8)}\frac{\Gamma(2+5)}{\Gamma(2)}\frac{\Gamma(2+3)}{\Gamma(2)}\biggr)\cdot \biggl(\frac{\Gamma(2)}{\Gamma(2+5)}\frac{\Gamma(1+4)}{\Gamma(1)}\frac{\Gamma(1+1)}{\Gamma(1)} \biggr) \\
& \;\;\;\cdot \biggl(\frac{\Gamma(2)}{\Gamma(2+3)}\frac{\Gamma(1+1)}{\Gamma(1)}\frac{\Gamma(1+2)}{\Gamma(1)}\biggr)\\
&= 7.2150\times 10^{-6}
\end{align}
となり、$m_1$のスコアを求める事が出来ました。
同様に$m_2$のスコアを計算していきます。
計算の詳細は省略しますが、以下のようになります。
\begin{align}
P(D|m_2) & = \biggl(\frac{\Gamma(4)}{\Gamma(8+4)}\frac{\Gamma(5+2)}{\Gamma(2)} \frac{\Gamma(3+2)}{\Gamma(2)}\biggr)\cdot \biggl(\frac{\Gamma(4)}{\Gamma(8+4)}\frac{\Gamma(5+2)}{\Gamma(2)} \frac{\Gamma(3+2)}{\Gamma(2)}\biggr)\\
&= 6.7465\times 10^{-6}
\end{align}
$P(D|m_1)$と$P(D|m_2)$を比較すると$P(D|m_1)$のスコアの方が高いのでこちらの構造$m_1$を採用するのが良いという結論になります。
後は$Y\to X$へエッジが向いている構造も考えて同様の計算を行えば全てのネットワーク構造のスコアの比較が行えます。
上の例では2変数だけだったので考えられる構造を全て列挙することが可能でしたが変数の数が増えると指数関数的に構造の候補数が増えてしまいます。
このスコアの計算はQUBOの定式化でも必要になります。
上記のスコアを計算する上で重要だったのはある確率変数の親がどのような確率変数で構成されるかという点です。
確率変数間に親子関係が存在すると、親から子へ有向エッジが貼られることになります。
有向エッジの貼り方によりスコアの値が決まります。
量子アニーリングでの最適化ではこのスコアを最大化するような有向エッジの貼り方を求めることになります。
QUBOの定式化
少々長くなりましたがベイジアンネットワークの基礎事項についての説明が終わりました。
これからは最適なベジアンネットワークの構造を決定するためのQUBOの定式化について説明していきます。
QUBOは次の3つのパートから構成されています。
- Score Hamiltonian: スコア最大化を大なうためのハミルトニアン
- Max Hamiltonian: 変数の親の候補数を制限するためのハミルトニアン
- Acyclicity Hamiltonian: DAGを保証するためのハミルトニアン
これらの定式化について順番に説明していきます。
$$
\def\bm#1{\boldsymbol{#1}}
$$
変数の定義
目的は確率変数に対応したノードがありノード間にどのような向きでエッジを貼っていくかを決めることです。
よって次のように有向エッジを変数として定義する必要があります。
\begin{align}
\def\bm#1{\boldsymbol{#1}}
\bm{d}=\{d_{ij}\in \{0,1\}:1\le i \le j \le n\; (i\neq j)\}
\end{align}
$d_{ij}=1$の場合は$X_i$から$X_j$に有向エッジが貼られていることを意味します。
有向グラフについて考えているので$d_{ij}$と$d_{ji}$は区別する必要があります。
よって確率変数の数が$n$個の場合、必要な$d$の要素数は$n(n-1)$個になります。
またこれらの定式化を行う上でそれぞれ以下の補助変数を導入する必要が出てきます。
- Score Hamiltonian: 高次項のリダクションに対する補助変数。
- Max Hamiltonian: 整数範囲の不等式制約に対する補助変数。
- Acyclicity Hamiltonian: 変数間の順序関係を表すための補助変数。
Score Hamiltonian
確率変数$X_i$の親の組み合わせを$J$とする。
$J$に応じてハミルトニアンの係数が定まる。
このハミルトニアンの係数が上で説明していたスコアに対応しています。
この値事後確率から計算でき、その係数を$w_i(J)$と定義します。
$w_i(J)$の計算方法について後で具体的に説明します。
このときのスコアハミルトニアンは、
\begin{align}
\mathcal{H}_{\text{score}} &:= \sum^n_{i=1}\mathcal{H}^{(i)}_{\text{score}}(\bm{d}_i) \\
\mathcal{H}^{(i)}_{\text{score}}(\bm{d}_i) &:= \sum_{J\subset\{1,\dots, n\}\setminus\{i\}}\biggl(w_i(J)\prod_{j\in J}d_{ji} \biggr)
\end{align}
と定義することが出来ます。
$\mathcal{H}^{(i)}_{\text{score}}(\bm{d}_i)$は確率変数$X_i$に注目した時の局所的なスコアハミルトニアンである。
このハミルトニアンについて説明する。
親の組み合わせ$J$に含まれる親の数を$|J|$と表すことにする。
$|J|=1$の場合
\begin{align}
\sum_{J\subset\{1,\dots, n\}\setminus\{i\}}\biggl(w_i(J)\prod_{j\in J}d_{ji} \biggr) = \sum_{j(\neq i)}w_i(j)d_{ji}
\end{align}
となる。グラフで表すと以下のようになる。
QUBOを実装するにはあらかじめ$w_i(j,k)$を事後確率から計算しておく必要があります。

$|J|=2$の場合、
\begin{align}
\sum_{J\subset\{1,\dots, n\}\setminus\{i\}}\biggl(w_i(J)\prod_{j\in J}d_{ji} \biggr) = \sum_{j,k(\neq i, j \neq k)}w_i(j,k)d_{ji}d_{ki}
\end{align}
となる。グラフで表すと以下のようになる。

後で具体的に計算して示しますが、一般的に
\begin{align}
w_i(j, k) \neq w_i(j) + w_i(k)
\end{align}
であることに注意する必要があります。
$|J|=3$の場合、
\begin{align}
\sum_{J\subset\{1,\dots, n\}\setminus\{i\}}\biggl(w_i(J)\prod_{j\in J}d_{ji} \biggr) = \sum_{j,k,l(\neq i, j \neq k\neq l)}w_i(j,k, l)d_{ji}d_{ki}d_{li}
\end{align}
となる。
3次項が含まれるため補助ビットを導入して2次以下にリダクションする必要がある。
次は$w_i(J)$の計算方法について説明します。
wの計算方法
事後確率の対数をとったものをスコア関数と呼ぶ。
スコア関数の最大化を行うのが目的であるが、量子アニーリングでは最小化問題を解くので全体にマイナスをつける必要がある。
これに注意するとスコア関数は
\begin{align}
s(B_S) :&= \sum^n_{i=1}s_i(\Pi_i(B_S)) \\
s_i(\Pi_i(B_S)) &= -\log{\biggl(\prod^{q_i}_{j=1}\frac{\Gamma(\alpha_{ij})}{\Gamma(N_{ij} + \alpha_{ij})}\prod^{r_i}_{k=1}\frac{\Gamma(N_{ijk} + \alpha_{ijk})}{\Gamma(\alpha_{ijk})}\biggr)}
\end{align}
と表すことが出来る。
$\Pi_i(B_S)$は$B_S$における確率変数$X_i$の親の集合を表す。$s_i(\Pi_i(B_S))$は確率変数$X_i$に注目した時の局所的なスコア関数である。このスコア関数の値を計算するには確率変数$X_i$の親の数$|J|$を設定する必要がある。
$|J|$を決めた時に$\mathcal{H}^{(i)}_{\text{score}}(\bm{d}_i)$が$s_i(\Pi_i(B_S))$と一致するように$w_i(J)$を求める必要がある。
確率変数$X_i$に注目して$w_i(J)$を計算していく。
$|J|=0$の場合は$w_i(\emptyset)$と表記し、$w_i(\emptyset)=s_i(\emptyset)$である。
この場合、確率変数$X_i$に親が存在しないことを意味するので、上の例で紹介したような計算を行えば値が求まる。
J=1の場合
$|J|=1$の場合、$d_{ji}=1$とするとスコアハミルトニアンは、
\begin{align}
\mathcal{H}^{(i)}_{\text{score}}(\bm{d}_i) &= w_i(\emptyset) + w_i(\{j\})
\end{align}
である。これが$s_i({X_j})$と一致することから、
\begin{align}
w_i(\{j\}) &= s_i(\{X_i\}) - w_i(\emptyset) \nonumber\\
&= s_i(\{X_j\}) - s_i(\emptyset)
\end{align}
となる。
J=2の場合
$|J|=2$の場合、$d_{ji}=d_{ki}=1$とするとスコアハミルトニアンは、
\begin{align}
\mathcal{H}^{(i)}_{\text{score}}(\bm{d}_i) &= w_i(\emptyset) + w_i(\{j\}) + w_i(\{k\}) + w_i(\{j, k\})
\end{align}
である。これが$s_i({X_j, X_k})$と一致することから、
\begin{align}
w_i(\{j, k\}) &= s_i(\{X_j, X_k\}) - w_i(\{j\}) - w_i(\{k\}) -w_i(\emptyset) \nonumber \\
&= s_i(\{X_j, X_k\}) - (s_i(\{X_j\}) - s_i(\emptyset)) - (s_i(\{X_k\}) - s_i(\emptyset)) - s_i(\emptyset) \nonumber \\
&= s_i(\{X_j, X_k\}) - s_i(\{X_j\}) - s_i(\{X_k\}) + s_i(\emptyset)
\end{align}
となる。
これより
\begin{align}
w_i(\{j, k\}) \neq w_i(\{j\}) + w_i(\{k\})
\end{align}
であることが分かる。
一般のJの場合
$|J|\ge 3$についても同様に計算することが出来る。
上記の計算を繰り返していくと$w_i(J)$の一般式は、
\begin{align}
w_i(J) = \sum^{|J|}_{l=0}(-1)^{|J|-1}\sum_{\substack{K\subset J\\ |K|=l}}s_i(K)
\end{align}
と表すことが出来る。
$|J|=m$の$w_i(J)$を計算するには$|J|=m-1$の$w_i(J)$が既に計算されている必要がある。
最大の親の数$|J|$はハイパーパラメータとして設定する必要がある。
$|J|=m$を最大の親の数とすると、
\begin{align}
\mathcal{H}^{(i)}_{\text{score}}(\bm{d}_i) &:= \sum_{\substack{J\subset\{1,\dots, n\}\setminus\{i\}\\ |J|\le m}}\biggl(w_i(J)\prod_{j\in J}d_{ji} \biggr)
\end{align}
となる。
Max Hamiltonianでは指定した親の数$m$を超えないような制約条件を追加する。
Max Hamiltonian
指定した親の上限数$m$を超えないような不等式制約条件を追加する必要がある。確率変数$X_i$の親の数は、
\begin{align}
d_i := |\bm{d}_i| = \sum_{\substack{1\le j \le n\\ j\neq i}}d_{ji}
\end{align}
で表すことが出来る。これに対して、
\begin{align}
d_i \le m
\end{align}
となる制約条件をQUBOで表せば良い。この論文ではバイナリエンコーディングで整数を表現している。
補助変数$y_i$を、
\begin{align}
y_i &:= \sum^{\mu}_{l=1}2^{l-1}y_{il} \\
\mu &= \lceil \log_2{(m+1)} \rceil
\end{align}
導入すればMax Hamiltonianは、
\begin{align}
\mathcal{H}_{\text{max}} &:= \sum^{n}_{i=1} \mathcal{H}^{(i)}_{\text{max}}(\bm{d}_i, \bm{y}_i) \\
\mathcal{H}^{(i)}_{\text{max}}(\bm{d}_i, \bm{y}_i) &:= \delta^{(i)}_{\text{max}}\biggl(m - d_i - y_i \biggr)^2
\end{align}
と表すことが出来る。
Acyclicity Hamiltonian
ベイジアンネットワークは有効非循環グラフ(DAG)である必要があります。
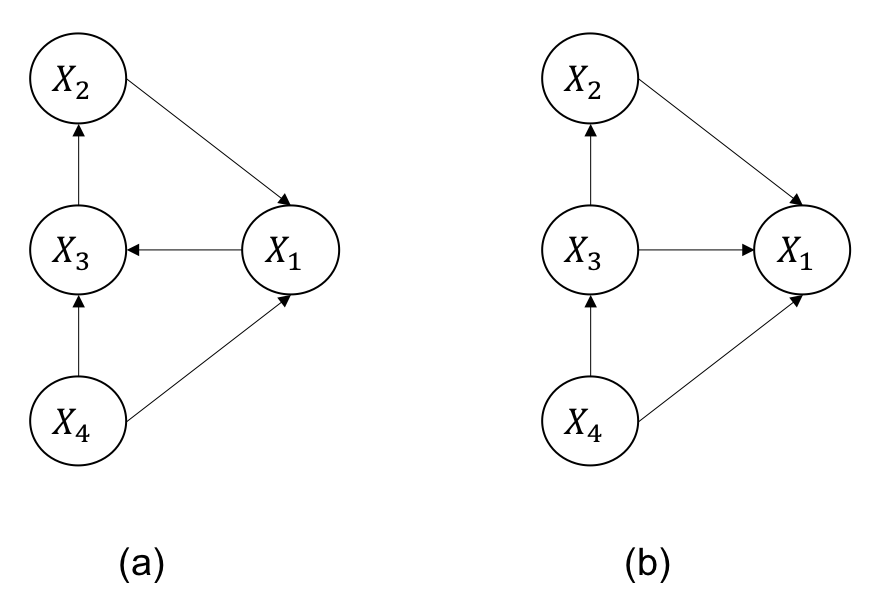
下図(a)に現れる循環閉路($X_2\to X_1\to X_3 \to X_1$)を禁止する必要があります。
変数間の順序関係を表現するために"$\le$"という記号を導入します。
これはTopological Orderと呼ばれており、$X_i$が$X_j$に対して親側のノードに含まれている場合、$X_i\le X_j$を意味します。
有向グラフが与えられた後にこの順序に並び替えるソート手法をTopological Sortと呼びます。
上図(b)をTopological Orderで表現すると
\begin{align}
X_4 \le X_3 \le X_2 \le X_1
\end{align}
になります。
一方で上図(a)は
\begin{align}
X_4 \le X_1 \le X_3 \le X_2 \le X_1
\end{align}
となります。
循環閉路が発生していると上記のように同じ変数$X_1$が2回以上登場しています。
順序関係を表したときに同じ変数が2回以上出現しているかどうかでDAGかそうでないかを区別することが出来ます。
この対応関係を表現するために次の$r_{ij}$を導入します。
\begin{align}
r_{ij} := \begin{cases}
1 & (X_i\le X_J) \\
0 & (X_i \le X_j)
\end{cases}
\end{align}
上図(a)の場合、
\begin{align}
r_{43} = r_{42} &= r_{41} = 1 \\
r_{32} &= r_{31} = 1 \\
r_{21} &= 1 \\
(\text{otherwise}&\;\; r_{ij} = 0)
\end{align}
上図(b)の場合、
\begin{align}
r_{43} = r_{42} &= r_{41} = 1 \\
r_{13} &= r_{12} = 1 \\
r_{32} &= r_{31} = 1 \\
r_{21} &= 1 \\
(\text{otherwise}&\;\; r_{ij} = 0)
\end{align}
となる。
3つの確率変数$X_i, X_j, X_k$に注目して
\begin{align}
X_i \le X_j \le X_k \le X_i\;\;\;(DAG1)\\
X_i \ge X_j \ge X_k \ge X_i\;\;\;(DAG2)
\end{align}
のいずれかが生じているとDAGではないことが分かる。
4変数以上のグラフに関してもその中から異なる3つを選んで順序関係を書き出すと、DAGではない場合上の順序関係が成立してしまう組み合わせが存在する。

上図を例に考えてみる。
上図の変数から異なる3つの変数の選び方は$(X_i, X_j, X_k), (X_j, X_k, X_l), (X_k, X_l, X_i), (X_l, X_i, X_j)$の4通りである。
それぞれの順序関係を表すと、
\begin{align}
X_i \le X_j \le X_k \le X_i \\
X_j \le X_k \le X_l \le X_j \\
X_k \le X_l \le X_i \le X_l \\
X_l \le X_i \le X_j \le X_l
\end{align}
となり、いずれも条件に違反することになる。
つまり、4変数であっても全体の順序から3変数だけ
\begin{align}
X_i \le X_j \le X_k \le X_l \le X_i \to X_i \le X_j \le X_k \le X_i
\end{align}
のように切り取って調べていけば良い。
以上より、3変数の順序関係が(DAG1), (DAG2)のいずれを満たすときにコストが生じるようなハミルトニアンを定義すれば良い。
これを実現させるために以下のハミルトニアンを定義します。
\begin{align}
\mathcal{H}^{(ijk)}_{\text{trans}}(r_{ij},r_{ik}, r_{jk}) &:= r_{ij}r_{jk}(1-r_{ik}) + (1-r_{ij})(1-r_{jk})r_{ik} \nonumber \\
&= r_{ik} + r_{ij}r_{jk} - r_{ij}r_{ik} - r_{jk}r_{ik} \\
&= \begin{cases}
1 & ((DAG1) \vee (DAG2) \\
0 & (otherwise)
\end{cases}
\end{align}
係数を含めてハミルトニアン全体を
\begin{align}
\mathcal{H}_{\text{trans}}(\bm{r}) &:= \sum_{1\le i < j \le n} \mathcal{H}^{(ijk)}_{\text{trans}}(r_{ij},r_{ik}, r_{jk}) \\
\mathcal{H}^{(ijk)}_{\text{trans}}(r_{ij},r_{ik}, r_{jk}) &:= \delta^{(ijk)}_{\text{trans}}\biggl( r_{ij}r_{jk}(1-r_{ik}) + (1-r_{ij})(1-r_{jk})r_{ik} \biggr)
\end{align}
と定義する。
最後に$d_{ij}$と$r_{ij}$がコンシストである必要があることに注意する。
$d_{ji}=1$の場合、$X_j\to X_i$へとエッジが伸びている。
一方でこの時、$r_{ij}=1$になったとすると、$X_i \le X_j$なので$X_i \to X_j$へとエッジが伸びていることになり両者の関係が矛盾する。
この場合、同時に両方の変数が1にならないような制約条件を追加する必要がある。
つまり$r_{ij}=d_{ji}=1$と$r_{ij}=1- d_{ij}=0$となる場合にコストが増加するようにハミルトニアンを定義する。
これを実現させるハミルトニアンは、
\begin{align}
\mathcal{H}_{\text{consist}}(\bm{d}, \bm{r}) &:= \sum_{1\le i < j\le n} \mathcal{H}^{(ij)}_{\text{consist}}(d_{ij}, d_{ji}, r_{ij}) \\
\mathcal{H}^{(ij)}_{\text{consist}}(d_{ij}, d_{ji}, r_{ij}) &:= \delta^{(ij)}_{\text{consist}} (d_{ji}r_{ij} + d_{ij}(1-r_{ij}))
\end{align}
となる。
以上より、DAGを保証するためのハミルトニアンは、
\begin{align}
\mathcal{H}_{\text{cycle}}(\bm{d}, \bm{r}) &:= \mathcal{H}_{\text{trans}}(\bm{r}) + \mathcal{H}_{\text{consist}}(\bm{d}, \bm{r})
\end{align}
となる。
補助変数の個数
以上で最適化に必要なQUBOの定式化が出来ました。
それぞれの項で新たに必要になる補助変数の個数についてまとめました。
Score Hamiltonian
$m$次項のリダクションで必要となる。
$m$次項を2次項にリダクションするには$(m-2)$個の補助変数が必要になる。1変数に対して3次から$m$次項までをリダクションする補助ビットが必要になるので、
\begin{align}
\sum^{m}_{n=3}(n-2) = \frac{(m-1)(m-2)}{2}
\end{align}
となる。これが変数の個数$n(n-1)$個に対して必要なので、
\begin{align}
\frac{n(n-1)(m-1)(m-2)}{2}
\end{align}
Max Hamiltonian
親の上限が$m$の場合、
\begin{align}
\mu &= \lceil \log_2{(m+1)} \rceil
\end{align}
$\mu$個の補助変数が1確率変数あたりに必要である。全部で$n$個の確率変数が存在するので$n\mu$個の補助変数が必要である。
Acyclicity Hamiltonian
$r_{ij}$の個数である$n(n-1)/2$個のだけ補助変数が補助変数が必要になる。
最後に
論文ではD-Wave2で実装可能なサイズである$n=7,m=2$のモデルに対して、その論理量子ビットの配置方法がグラフィカルに図示されていました。

ただ古典手法との性能比較などは記載されていませんでした。
扱える問題の規模が小さいのでマトまな比較にならないのかもしれません。
論文ではさらに詳しくそれぞれのハミルトニアンに設定する係数の範囲についてまで議論されているので興味のある方はご覧ください。
課題としては親の上限を増やす連れてビット数が指数関数的に増えるので、ビットリソースと性能とのトレードオフが古典手法に対して優位性があるか検証が必要になると思います。