Rで時系列データを時系列解析する
モデルを推定し実測値と予測値を比較してみたら面白かったので、記事にしてみました。
さらに予測の精度が悪かった箇所を考察してみました。(2018/6/2更新)
主な参考文献は、田中考文著「Rによる時系列分析入門」です。
使用する時系列データは、経済産業省 鉱工業指数 集計結果より2008年1月から2016年12月までの酒類の総合原指数月次付加価値額生産(IIP)とします。
2017年の酒類のIPPは予測値と比較するために使用します。
なんとなく目についたので酒類にしてみました。
この時系列データを使って2017年の酒類のIIPを予測し、2017年の酒類のIPPを実測値として比較することで予測精度を確認してみます。
データの増減に規則性があり予測しやすそうですが、このグラフだけでは確証が持てません。
そのため時系列分析に向いている時系列データかどうか確認した上でモデルを推定していきます。
今回は以下の手順でモデルを推定し、実際に予測します。
- 時系列オブジェクトにする
- 時系列データの特徴を捉える
- 時系列データが定常過程かどうか確認する
- 自己相関・偏自己相関を確認する
- モデルを推定する
- 推定モデルを使って予測する
サンプルコードをまとめたものはこちら。
data.csvに2008年1月から2016年12月までの酒類のIIPを書き込んでおく必要があります。
# 時系列オブジェクト生成
data <- read.csv("data.csv")
IIP <- ts(data,start=c(2008),frequency=12)
# 要素分解
plot(decompose(IIP))
# ADF検定
library(tseries)
adf.test(IIP)
# 自己相関
acf(IIP,lag.max=96,ylim=c(-.2,1.0))
# 偏自己相関
pacf(IIP,lag.max=96,ylim=c(-.2,1.0))
# モデルの自動適合
# auto.arima関数からSARIMA(1,0,0)(0,1,2)[12]が推定される
library(forecast)
Fit <- auto.arima(IIP,ic="aic",trace=F,stepwise=F,approximation=F,allowmean=F,allowdrift=F);Fit
# モデルの推定
# 推定されたSARIMA(1,0,0)(0,1,2)[12]をarima関数で作成する
Model <- arima(IIP,order=c(1,0,0),seasonal=list(order=c(0,1,2),period = 12));Model
# 残差検定の診断
tsdiag(Model)
# 予測値の取得
Model.pred <- predict(Model,12)
value <- (Model.pred$pred);value
時系列オブジェクトにする
まずは使用するデータをcsvファイルにし、ts関数で時系列データを時系列オブジェクトにします。
data <- read.csv("data.csv")
IIP <- ts(data,start=c(2008),frequency=12)
時系列データの特徴を捉える
時系列データを3つの要素(トレンド+周期変動、季節変動、不規則変動)に分解しデータの特徴を捉えることで、時系列分析に向いているデータか確かめます。
各要素に対し以下の状態であれば時系列データの特徴を捉えることができます。
トレンド、周期変動、季節変動に以下の状態が見られれば時系列分析しやすい時系列データであるといえます。
| 要素名 | データの状態 | データの特徴 |
|---|---|---|
| トレンド | データが上昇,または下降している状態 | 長期間にわたり増加または減少する変化がある |
| 周期変動 | データが上昇と下降を繰り返している状態 | 一定の間隔で同じような増減の変化がある |
| 季節変動 | データが季節的変動を繰り返している状態 | 毎年同じような増減の変化がある |
| 不規則変動 | データの動きが時間の経過に依存しない状態 | 時間に関係なく増減する変化がある |
先ほどのグラフのように原データのままでは要素の特徴を捉えにくいため時系列データを分解する必要があります。
そこで、decompose関数を使うとトレンド+周期変動、季節変動、不規則変動をtrend、seasonal、randomとして分解することができます。
plot(decompose(IIP))
trendを見ると、酒類のIIPは長期的に減少傾向にあり、トレンドのあるデータだと判断できそう。
こうして見ると年々酒類の生産量は減っていることがわかります。
seasonalを見ると、酒類のIIPは毎年規則性のある変動を繰り返しており、季節変動のあるデータだと判断できそうです。
酒類のIIPは夏と12月に最も多く、1月に最も少ないという特徴が見られました。
時系列データが定常過程かどうか確認する
定常過程とは、平均や分散が時間変化せず時間的に変化しない一定の確率過程のことです。
分析したい時系列データが定常過程であればモデル推定の精度が良くなるといわれています。
定常過程であるか判断するには単位根過程でないことを確認する必要があります。
Rで計量時系列分析:単位根過程、見せかけの回帰、共和分、ベクトル誤差修正モデルによると
単位根過程とは、簡単に言うと時系列データは非定常過程だが差分を取った時系列データは定常過程である確率過程のことです。
今回はADF検定を行い、時系列データが定常過程かどうか確認します。
ADF検定とは、帰無仮説「過程が単位根である」が棄却されれば定常過程であるとする検定です。
今回はライブラリtseriesのadf.test関数を使ってADF検定を行います。
library(tseries)
adf.test(IIP)
上記のコードを実行すると以下の結果が得られます。
Augmented Dickey-Fuller Test
data: IIP
Dickey-Fuller = -5.8608, Lag order = 4, p-value = 0.01
alternative hypothesis: stationary
警告メッセージ:
adf.test(IIP) で: p-value smaller than printed p-value
p-valueが0.01以下であることから帰無仮説「過程が単位根である」が棄却され、酒類のIIPは定常過程であることが確認できます。
ひとまず、時系列分析に向いてそうな時系列データだということがわかりました。
さらに、ある時点のデータとの間に何らかの関係性があれば、次の年のIIPを正しく予測できそうです。
自己相関・偏自己相関を確認する
Rで計量時系列分析:はじめに覚えておきたいことによると
自己相関とは、同一時系列データの異時点間の相関関係を表す指標のことです。
偏自己相関係数とは、同一時系列データのある2つの時点間の直接の相関関係を表す指標のことです。
自己相関・偏自己相関のプロットを確認すると、時系列データが過去の各時点と相関関係があるかどうか確認できます。
相関関係があれば時系列分析に向いている時系列データだということが分かります。
自己相関はacf関数、偏自己相関はpacf関数にて確認することができます。
# 自己相関
acf(IIP,lag.max=96,ylim=c(-.2,1.0))
# 偏自己相関
pacf(IIP,lag.max=96,ylim=c(-.2,1.0))
上記のコードを実行すると以下のグラフを得られます。
自己相関は、Lagが1,2,3…と1ごとに95%の信頼区間(青い点線)を超える有意な相関があります。
これはある時点と1年ごとのデータに強い相関が見られ、一定間隔でデータ間に強い関係性があると考えられます。
偏自己相関は、Lagが1に95%の信頼区間(青い点線)を超える有意な相関があります。
これはある時点と1年前のデータ間に強い相関が見られ、年ごとのデータ間に強い関係性があると考えられます。
一定間隔で相関が見られることから周期変動があるデータであると考えられます。
さらに1年ごとの相関となると季節変動があるデータとも考えられます。
モデルを推定する
上記で酒類のIIPが時系列分析に向いていることが分かりました。
いよいよモデルを推定していきます。
ライブラリforecastのauto.arima関数でモデルを自動推定します。
今回モデルを推定する基準はAICを用います。
各引数の説明は、R Documentation auto.arima functionを参考にしてください。
library(forecast)
# モデルの自動適合
Fit <-auto.arima(IIP,ic="aic",trace=F,stepwise=F,approximation=F,allowmean=F,allowdrift=F);Fit
自動推定した結果がこちら。
Series: IIP
ARIMA(1,0,0)(0,1,2)[12]
Coefficients:
ar1 sma1 sma2
-0.2400 -0.0572 0.3041
s.e. 0.1054 0.1118 0.1769
sigma^2 estimated as 26.86: log likelihood=-293.86
AIC=595.71 AICc=596.15 BIC=605.97
今回推定されたモデルは$SARIMA(1,0,0)(0,1,2)_{12}$となりました。
ただし、推定されたモデルが適切であるかどうかきちんと確認する必要があります。
そこで、残差に自己相関が無い適切なモデルか判断します。
残差に自己相関が無いか判断するには、残差の自己相関を確認し、Liung-Box検定を行います。
【R】時系列データに関する基本的な検定【統計】によると、
Liung-Box検定とは、帰無仮説「残差に自己相関が無い」が棄却されなければモデルが適切であるとする検定です。
先ほど推定された$SARIMA(1,0,0)(0,1,2)_{12}$をarima関数で作成し、tsdiag関数で残差に自己相関が無いか確認します。
Model <- arima(IIP,order=c(1,0,0),seasonal=list(order=c(0,1,2),period = 12));Model
# 残差検定の診断
tsdiag(Model)
Call:
arima(x = IIP, order = c(1, 0, 0), seasonal = list(order = c(0, 1, 2), period = 12))
Coefficients:
ar1 sma1 sma2
-0.2400 -0.0572 0.3041
s.e. 0.1054 0.1118 0.1769
sigma^2 estimated as 26.02: log likelihood = -293.86, aic = 595.71
Rと時系列によると、
この図は、上から残差のプロット、残差の自己相関のプロット、Ljung-Box検定のp値のプロットになります。
残差の自己相関のプロットよりLag0.0のACF以外に95%の信頼区間(青い点線)を超える有意な相関がなく、残差に有意な自己相関がないことがわかります。
Ljung-Box検定のp値のプロットより全てのLagに対するp値において95%の信頼区間(青い点線)を超え、Liung-Box検定が棄却されないことがわかります。
よって、残差に自己相関が無い適切なモデルであることが分かりました。
推定モデルを使って予測する
先ほど推定したモデルを使って2017年の月別酒類のIIPを予測してみましょう。
Model.pred <- predict(Model,12).pred
value <- (Model.pred$pred);value
実行結果はこちら。
Jan Feb Mar Apr May Jun Jul
2017 56.09331 76.22289 93.17242 103.74415 82.17886 106.66486 96.41295
Aug Sep Oct Nov Dec
2017 92.24215 91.45305 90.10543 100.02132 126.86665
この予測値と実際に経済産業省で集計された酒類のIIPを比較したものが下のプロットです。
実線が実際の値、点線がモデルの予測値になります。
一部精度が悪い箇所がありますが概ね良い予測ができました。
因みに自動推定した後に予測結果を得たい場合はforecast関数を用いると便利です。
plot(forecast(Fit))
forecast関数の実行結果のプロットはこちら。
2018年まで予測してくれています。
何故、精度が低い箇所が出来てしまったのか
どの箇所の精度が悪いのか
予測値と2017年の酒類のIIPを比較したプロットを見てみます。
春頃の予測の精度が悪いようです。
次は実測値と予測値の差、残差の絶対値を見てみます。
特に2017年4月から2017年6月までの予測の精度が悪いことが分かります。
| 年・月 | 実測値 | 予測値 | 残差の絶対値 |
|---|---|---|---|
| 2017・01 | 55.4 | 56.09331 | 0.69331 |
| 2017・02 | 76.1 | 76.22289 | 0.12289 |
| 2017・03 | 95.3 | 93.17242 | 2.12758 |
| 2017・04 | 93.8 | 103.74415 | 9.94415 |
| 2017・05 | 97.4 | 82.17886 | 15.22114 |
| 2017・06 | 98.3 | 106.66486 | 8.36486 |
| 2017・07 | 94.9 | 96.41295 | 1.51295 |
| 2017・08 | 91.1 | 92.24215 | 1.14215 |
| 2017・09 | 86.1 | 91.45305 | 5.35305 |
| 2017・10 | 88.7 | 90.10543 | 1.40543 |
| 2017・11 | 98.6 | 100.02132 | 1.42132 |
| 2017・12 | 123.6 | 126.86665 | 3.26665 |
4月から6月までのデータの特徴が変わった可能性が考えられます。
データの特徴が変わったのか
2008年から2017年の実測値のプロットを見てみます。
確かに2017年の春頃の実測値の増減は例年に比べ穏やかになっていることが分かります。
decompose関数を使ってデータの特徴が変わったのか見てみます。
左図は2008年から2017年の実測値を用いたもので、右図は2008年から2016年の実測値を用いたものです。
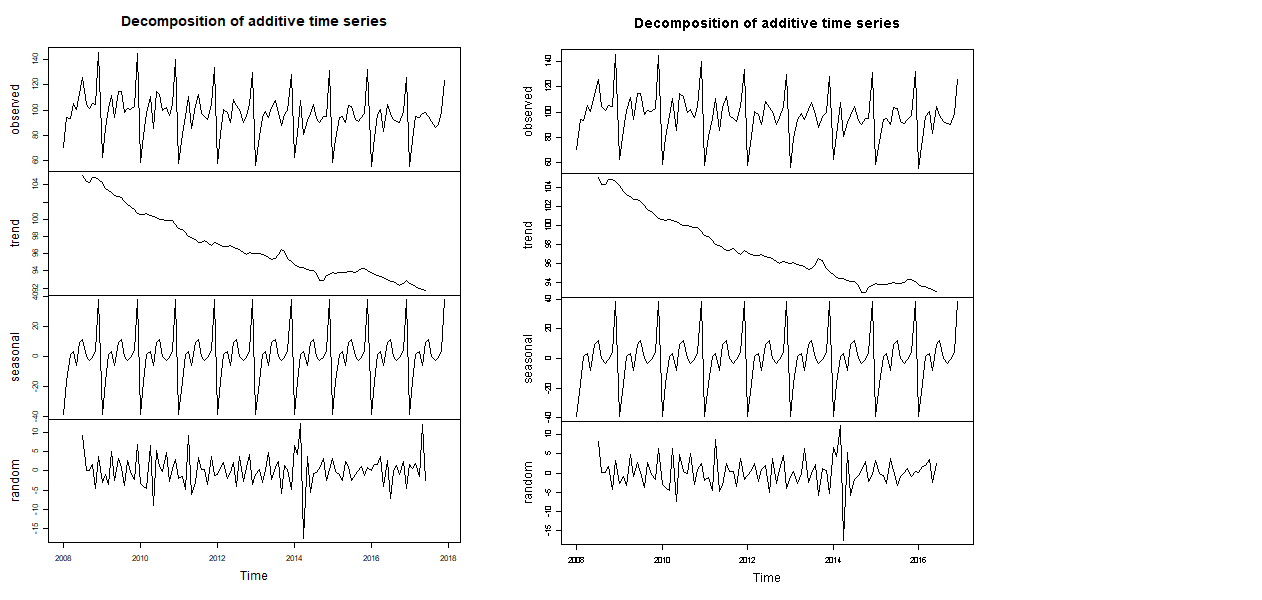
トレンドや季節変動はあまり変わりませんが、不規則変動が大きく変動していることが分かります。
結論
2017年の4月から6月までのデータの増減が過去の特徴と異なっているため上手く予測できなかったと考えられます。
2017年の4月から6月にトレンド、周期変動、季節変動以外の原因で何か増減に変化が出ることが起こったのではないかと考えられます。
2017年に酒関連のニュースを探してみると2017年4月の酒税法の改正がありました。酒税法の改正により酒類のIPPに何らかの影響があったと考えられます。
2016年の実測値と2017年の予測値が似ている?
因みに2016年の実測値と予測値を比べるとかなり似ています。
つまり、このモデルでは2017年の酒類のIIPは2016年の値とそれほど変わらないと予測していたことが分かります。









