これ何
このアドベントカレンダーはすっげーフリーダムな世界観のようなので、知り合いからリクエストのあった、OpenGLの非常にざっくりとした入門記事みたいなものを書きます。
申し訳ないことに題材を準備するのをうっかりしていたので、現在、趣味で制作しているものの基礎的な部分を解説しながら、チュートリアルとさせてもらう事になります。
OpenGLは同次座標系など3D特有の数学が頻繁に使われますが、このチュートリアル内ではそういうものは省きながらも、初心者にはそこそこの歯ごたえがあるくらいの内容を目指します。
では、早速始めていきます。
開発環境について
ShaderToyをつかいます。
このサイトはシェーダに渡す元画像の設定などが比較的に簡単にできて、また、エディタも比較的使いやすいと思っているのでおすすめです。
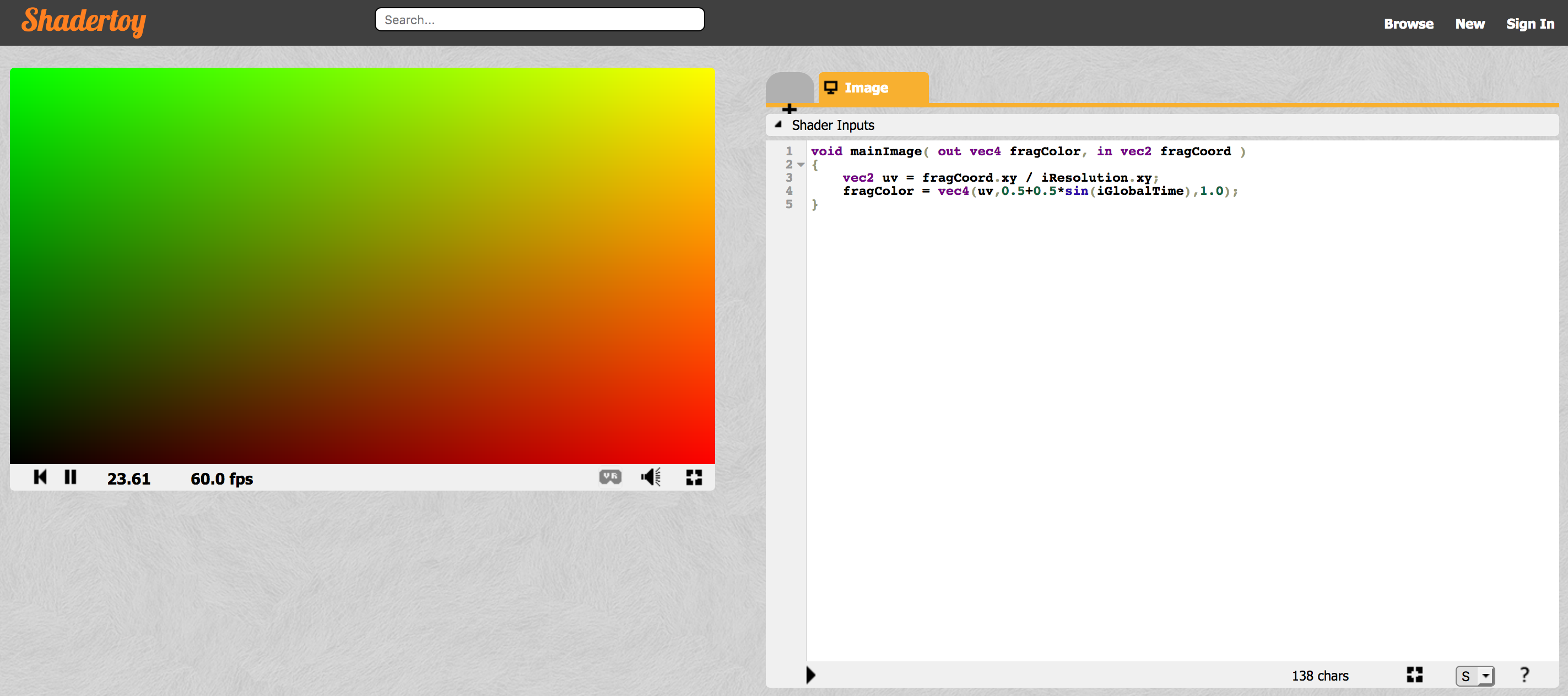
右上の方の「New」と書いてあるところをクリックすれば次のような画面になると思います。
実はなんと!この画面が表示された時点で、あなたはもう既にOpenGLのプログラムを実行することに成功しています!
右側がシェーダーのプログラムで、左側はそのレンダリング結果です。
プログラム内の定数を自由にいじってみて、エディタの下の方にある矢印ボタンを押してみましょう。左側のレンダリング結果が変わるのがわかると思います。
ちょっといじってみて、エディタの基本的な使い方がわかったら、次のステップへと進みましょう。
目標のもの
水面やガラスの屈折のようなものを作ります。
画像をみると、凸凹したガラスの奥にロンドンの風景があるように見えてきませんか?
(いまいち伝わらない理由はお察しください)
今回はこれが目標です。
プログラミングのモデル
まずはどのようにOpenGLでのプログラミングがなされるのかを説明します。
OpenGLのシェーダーのプログラムを記述するのには、GLSLという言語が用いられます。
このチュートリアル内では、組み込み型で2,3,4次元のベクトル型があること以外は、GLSLはC言語だと思っていいです。
ちなみにベクトル型は構造体のように扱うことができます。
つまるところC言語でプログラミングできるのですが、では具体的にどうやって絵を作るのかといいますと、
我々がGLSLのコードを書いて実行すると、OpenGLは「このピクセルの色は何色にしてほしいか?」という質問を投げてくるので、それに答えるプログラムを書けば良いということになります。
ShaderToyでデフォルトで実行されるコードについて見てみましょう。
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = fragCoord.xy / iResolution.xy;
fragColor = vec4(uv,0.5+0.5*sin(iGlobalTime),1.0);
}
fragCoordは色を尋ねられているピクセルの位置です。
何らかの計算をして、fragColorに結果の色を書き出してやることで、そのピクセルの色を自由に決めることができます。
また、fragColorはr,g,b,aの4つの色の要素のベクトルです。
上のプログラムでiResolutionは画面の解像度、iGlobalTimeは時刻を表すグローバル変数です。ここまで解説すると、上のプログラムが何をしているのか、どのような絵が作られるのか想像がつくのではないでしょうか。
大きな座標に行くと赤と緑が強くなっていき時間によって青みが変わるということです。
素材となる画像を読み込む
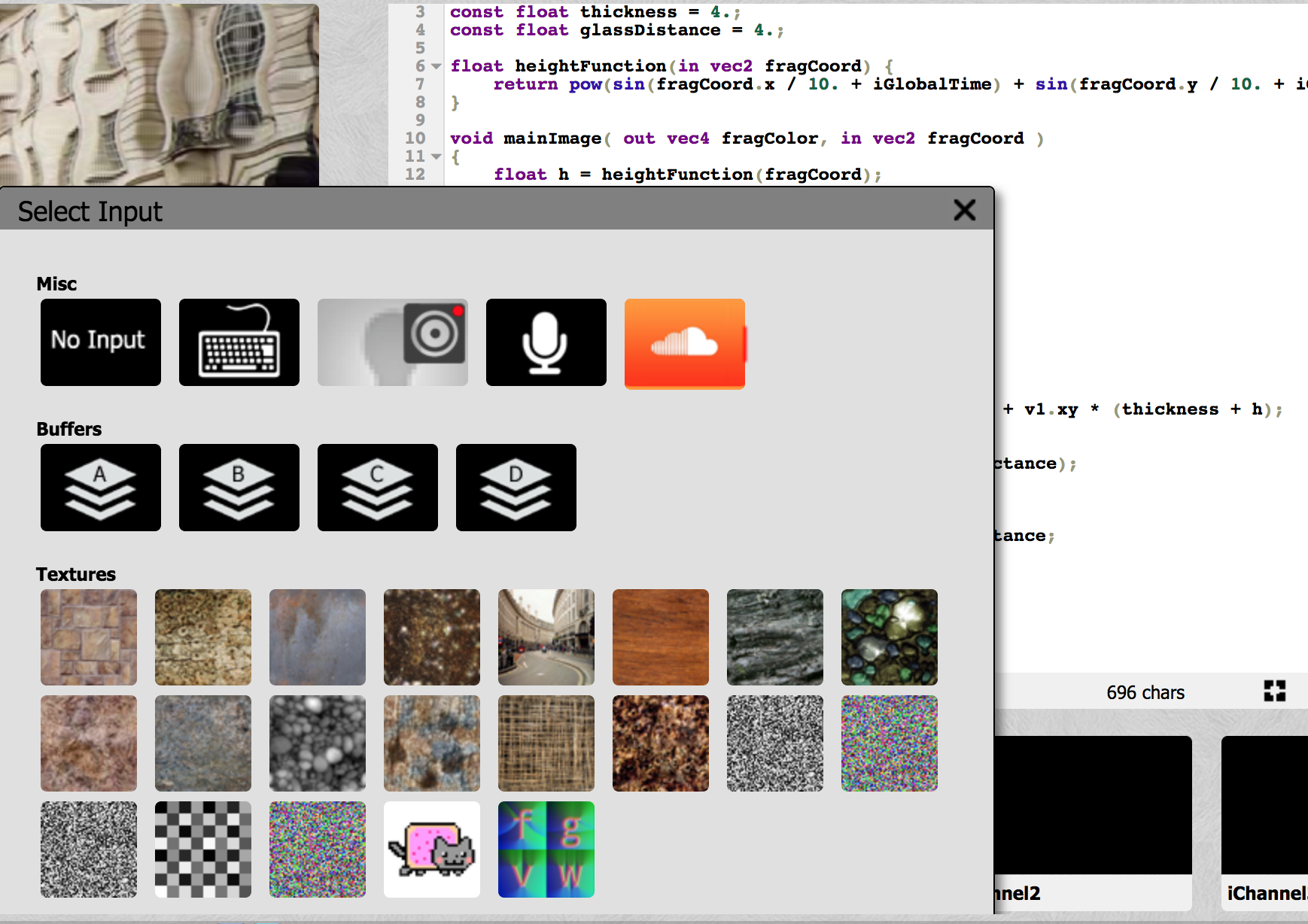
まず、エディタの下にあるiChannel0という欄をクリックして、Texturesの欄から、好きな画像を選びましょう。
これを行うことで、シェーダープログラムの中でこの画像を参照できるようになります。
では、この画像をそのまま表示するプログラムを書いてみましょう。
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = fragCoord.xy / iResolution.xy;
fragColor = texture2D(iChannel0, uv);
}
最初のプログラムとfragColorの部分が変わっています。
texture2Dと言うのは画像と座標から、色を持ってくる関数だと思ってください。
(texture2Dは座標として0〜1の間の値を取ります。そのためにflagCoordをiResolutionで割っています)
つまり、これはOpenGL側から尋ねられた座標に対して、画像の対応する位置の色をそのまま結果にするプログラムであることがわかります。
矢印ボタンを押してみましょう。あなたの選んだ画像がそのまま表示されるはずです。
屈折の原因となる素材の形状を表現する
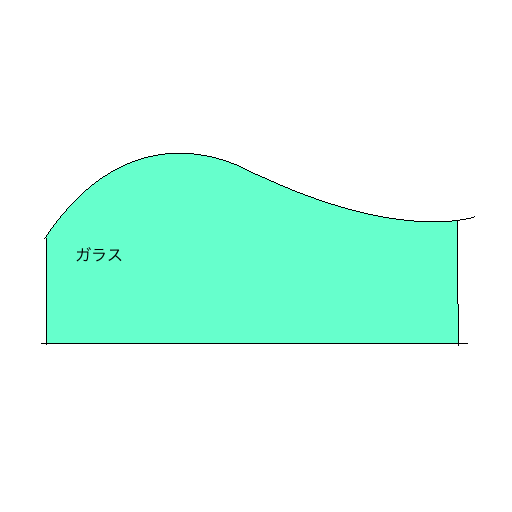
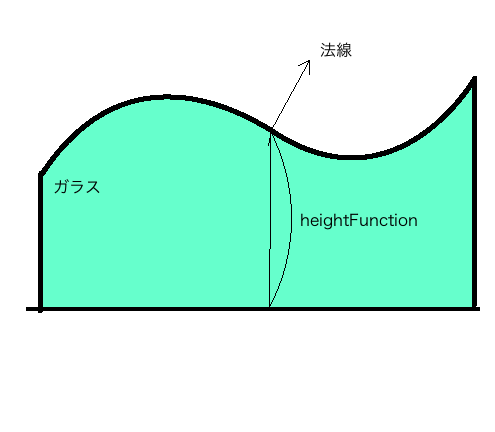
下のような形の物体の表面について考えます。
ある点で、基準となる面からどれくらい盛り上がっているか表現することができれば、表面の形状を表現することに成功しているといえます。
ここでは具体的に次のように表現します。
float heightFunction(in vec2 fragCoord) {
return pow(sin(fragCoord.x / 10. + iGlobalTime) + sin(fragCoord.y / 10. + iGlobalTime), 2.) * 0.01;
}
これが山が格子状に並んだ形を表していることがわかってもらえますでしょうか。
わかりにくい場合は可視化すると良いです。次のようにしてみましょう。
float heightFunction(in vec2 fragCoord) {
return pow(sin(fragCoord.x / 10. + iGlobalTime) + sin(fragCoord.y / 10. + iGlobalTime), 2.);
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec3 color = vec3(heightFunction(fragCoord));
fragColor = vec4(color, 1.);
}
高い部分が白色として、低い部分が黒色として表現されています。今回はこの形を使って、屈折表現に挑戦します。
法線ベクトルを取り出す
「偏微分」を使います
微分と聞いて怖くなった方もいらっしゃると思いますが、そんなに怖いものではありません。
x軸方向、y軸方向で隣り合うピクセルの計算結果との差分を取ってくるだけです。つまり、隣のピクセルとの計算結果と引き算するだけです。
ここで偏微分をするためにはdFdx, dFdyという関数を使います。使い方は次のようになります。
float h = heightFunction(fragCoord);
vec3 t1 = vec3(1., 0., dFdx(h));
vec3 t2 = vec3(0., 1., dFdy(h));
なんとも不思議な書き方ですが、このようにすると隣接するピクセルとの高さの差分を取ってくることができます。
ところでこのt1とt2は表面の線形独立な接線ベクトルとなっています。なのでt1とt2の外積を取ってきてやれば、その点での表面の法線を得ることができるようになるということです。
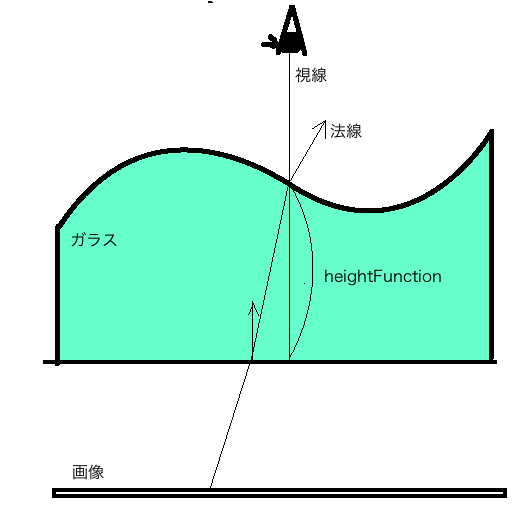
屈折の光をたどる
GLSLには組み込み関数として、屈折光の向きを計算する(!)refractという関数があります。なんともピンポイントですが、便利なのでこいつを使います。
向きさえわかれば、それを伸ばしてどこに突き当たるか求めるのはベクトルならばかんたんなことです。ごちゃごちゃやると以下のようになります。
const float refractance = 1.4;
const vec3 eyeVector = vec3(0., 0., -1.);
const float thickness = 4.;
const float glassDistance = 4.;
float heightFunction(in vec2 fragCoord) {
return pow(sin(fragCoord.x / 10. + iGlobalTime) + sin(fragCoord.y / 10. + iGlobalTime), 2.) * 0.01;
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
float h = heightFunction(fragCoord);
vec3 t1 = vec3(1., 0., dFdx(h));
vec3 t2 = vec3(0., 1., dFdy(h));
// 法線
vec3 n = normalize(cross(t1, t2));
// 表面での屈折
vec3 v1 = refract(eyeVector, n, refractance);
v1 /= v1.z;
// 裏面での位置
vec2 exitPoint = fragCoord.xy / iResolution.xy + v1.xy * (thickness + h);
// 裏面での屈折
vec3 v2 = refract(v1, vec3(0., 0., -1.), refractance);
v2 /= v2.z;
// 裏面から光を伸ばした先はどこ?
vec2 imagePoint = exitPoint + v2.xy * glassDistance;
// そこの画像の色を持ってくる
vec4 color = texture2D(iChannel0, imagePoint);
fragColor = color;
}
結果は...?
やりました!グニャグニャに歪んだ画像が現れました!
目標達成です。
この講座はここまでです。ありがとうございました。
最後に
ぶっちゃけ、自分で書いてて何が言いたいのか伝わらんだろうなあと思います。文章力の無さ。
「なんかよくわかんないけど、シェーダープログラミングで色々できそう!」と思ってもらえれば幸いです。
明日はGandTさんで、「出版甲子園でプログラミングの入門書を出版すると称して演説してきた結果」についてです。楽しみですね。