以下は、ある機械学習屋のボヤキである。
だれか、解決してくれる人がでてきてほしい。
サンプリング定理とは
標本化定理ともいう。
「標本化定理は、元の信号をその最大周波数の2倍を超えた周波数で標本化すれば完全に元の波形に再構成されることを示す。」
最大周波数の2倍を超えた周波数で標本化で十分であり、最大周波数の4倍の周波数で標本化(サンプリング)しても、追加で得られる情報はないことを意味する。
このことは、どこまでサンプリング頻度を高めれば十分なのかを言い切ってくれている。この定理があるからこそ、CDや時系列データの圧縮技術、DVD,Blu-ray, 動画配信が可能になっている。
機械学習に欠けているもの
その1: サンプリング定理に相当するものが不足している。
そのため、ポジティブサンプルをどれだけ密にサンプリングしなければならないのかを評価することができていない。
不足していること1:ポジティブサンプルのサンプリングの密度を計量する指標
不足していること2:その指標がどれくらいを上回っている(もしくは下回っていれば)、ポジティブサンプルの密度は十分なのかを判断する不等式。
その結果
- 学習結果の特徴量空間での連続性がどの程度確保されているのかがわからない。
- 敵対的なノイズを加えることで、推論を間違えさせることができるのは、そのような分類・検出の学習結果の連続性を確保できていないことを示している。
その2: サンプリングの空間の定義域の可視化
サンプリング定理の場合、関数の定義域がある。
しかし、機械学習の問題において、明確な定義域の存在するものは稀である。
学習のポジティブサンプルの定義域がどのようになっているのかがわからない。
例:自動車の検出
- 前方、側面、後方車両の自動車検出
- ドローンから検出する自動車検出
この2つの場合は、自動車の姿勢が異なる。すなわち、カバーする姿勢の定義域が異なっている。
しかし、現状の機械学習においては、個別のポジティブサンプルが与えられているだけで、どのようは範囲の定義域になっているかを知ることができない。
例:人検出の場合
- 人の目線の高さでの撮影画像での人検出
- 監視カメラなどの高い視点からの人検出
- エレベータなどの更に角度のある視点からの人検出
これらは、人検出としての定義域が異なる。
そのため、一方の用途の検出器は他方の用途には適さない。
検出器のモデルの比較をする際には、それがどのようなデータセットで訓練されているかを知ることだ。
(オープンのモデルの場合には、訓練データセットが公開されていることがある。
商用のモデルの場合だと、基本どのようなデータで訓練されているのかを知りようがない。
)
結果
ポジティブサンプルの定義域と、そのサンプリング密度がわからないため、ポジティブサンプルが十分な分布になっていることを確認できない。
お願い
- 機械学習の学習できている範囲を検証するポジティブサンプルの定義域を可視化できるような指標を見つけること。
- また、そのデータがどの程度の連続性を持っているのか、機械学習で十分な学習結果の再現性を満たすためには、どの程度を連続性を与えればいいのかを示す指標がほしい。
- 理論的な考察に腕の覚えがある人は、ぜひそのような理論を作ってほしい。
現状でのヒント
データの分布の可視化の取り組みには、t-SNE(=t分布型確率的近傍埋め込み法)
解説記事 t-SNEによる次元削減
パラメータの分布の連続性の確認
- 対象物によっては一部のパラメータが連続的に分布したり、離散的なパラメータがあったりする。
- 例:顔の見え方に対するパラメータ
- 回転角(roll, pitch, yaw)
- メガネの有無
- マスクの有無
- 学習データに対して、これらの分布を確認する。
CGデータによるパラメータ分布域の拡大
- CGデータを用いると、対象物の見え方の網羅性を改善できる。
- 例:顔の見え方に対するパラメータ
- 上記のパラメータの他に、以下のようなパラメータを増やすことができる。
− 光源の種類 - 光源の位置
- 顔の表情(口の開け具合など)
- 帽子の有無
- 髪型
こういったパラメータの組み合わせに対してCG画像をレンダリングしてデータを作ることで
実写だけではカバーしきれていない領域に対するデータを増やすことができる。
GANによるデータの分布域の拡大
- 実データに対するautoencoderは、実データをパラメータによって記述できるようにする。
- そのパラメータを元に逆に画像を生成させることができる。
- 単純に任意のパラメータで画像を生成させると、対象物らしくない画像を生成してしまう。
- そこで、対象物らしいものと対象物らしくないとを区別する。
- それがGANである。
- GANを使うと、学習させるデータの分布域を広げることができる。
このようにデータの分布域を広げることができる。
これらのようにデータの分布域の網羅性が重要なことがわかっている。
ただ、現状では、どのようにしたら、データの分布域・データの密度とを満たしているのかを確認するための
一般的な方法をまだ知らない。
追記(2023)
どうやら、期待する内容に近いのが、次のスライドの内容そうだ。
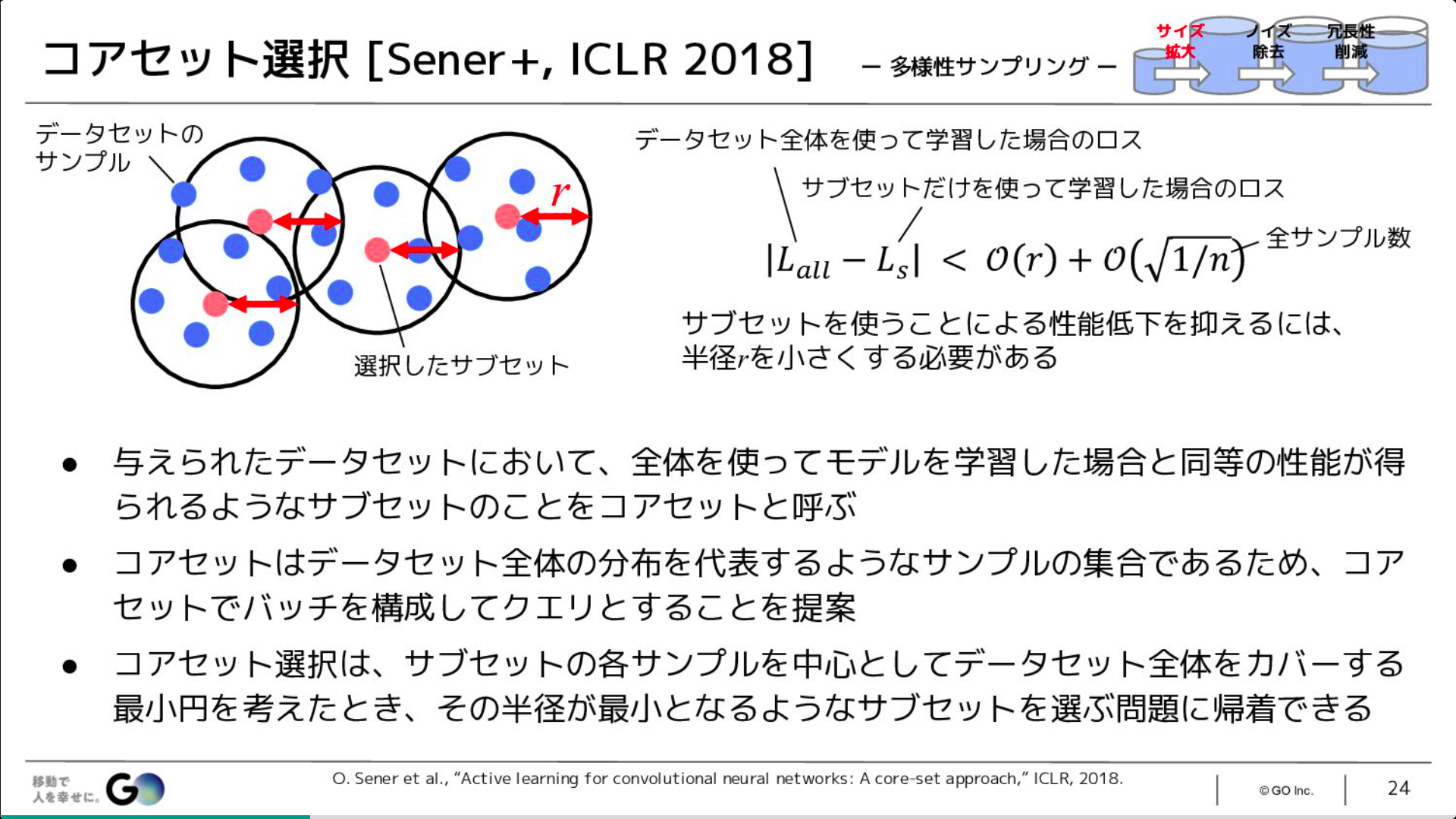
ある半径rでのサブセットで学習した場合の損失関数と
データセット全体を使って学習した場合の損失関数との差の絶対値が
右辺の値よりも小さくなるときに、
同等の性能が得られる。
Data-Centric AI - 関連する学術分野と実践例 のスライドから引用。
追記 2024.8.2
数式から自動生成した大規模画像データセットを用いて人工知能(AI)の画像認識モデル(学習済みモデル)を構築する手法
が発表されている。
このような手法によって、学習用のデータの分布が偏りが解消されるのではないか。
Replacing Labeled Real-image Datasets with Auto-generated Contours
https://hirokatsukataoka16.github.io/Replacing-Labeled-Real-Image-Datasets/
github
機械学習のタスクは最小化問題だ。
機械学習のその最小化問題をどう上手に解くかが機械学習に成功するコツだ。
最小化問題を解く例題の宝庫は物理学だ。
物理学では、多くの問題を異なる解き方で解く。
それは、対象を厳密に解くのが簡単じゃないからだ。
今回はその手法のなかから変分法を説明する。
変分法の説明を見てみよう
変分法は、汎函数の引数である関数のわずかな変化によって生じる小さな変動としての汎函数の変分に注目する。
変分法を前提として考えると、十分に最適化された近傍では、ある微少量の変動を加えても、一次変分は0になる。
つまり、微小な変分を加えても、汎関数は値が変わらない。
これを画像認識の機械学習のタスクに読み替えてみる。
・機械学習の損失関数は、学習サンプルのデータに対する汎関数である。
・機械学習は、その損失関数を関数を最小化するプロセスである。
・十分に安定な機械学習結果であれば、その近傍で微小な変動を加えても、画像認識の結果は安定した結論を返すべきであると考える。
機械学習の安定性をあげるには、微小な変動に対する安定性をあげることだ。
たぶん、見たことがあるだろう。
パンダの画像にノイスを与えると、別の分類になってしまうという事例を。
あなたの機械学習の結果の安定性を上げるには、元画像に対する微小変動を加えても
認識結果が影響を受けないようにすることだ。
損失関数の定義は、学習データを入力とする汎関数と考えることができる。
ここで、汎関数的な考え方がでてくる。
十分に最小化された汎関数であれば、微小な変動を加えても汎関数の微分は0になるべきであるということである。
パンダの画像へのノイズの付与は、解釈結果を劇的に変えてしまいうるという報告は、
畳み込みニューラルネットワークの学習が、微小な変動に対するロバスト性を前もっては用意してくれてはいない。
だから、自分の行う学習を改善するには、そのようなロバスト性の改善を自分で実装することとなる。
ロバスト性を改善するには
- 元画像に微小変動を加えた画像を、元画像ともに学習に加える。
- そうすれば、元画像と、微小変動を加えた画像とに対して共通な推定結果を返しやすい。
90度回転を加えてるのと、5度回転加えるのに違いがあるの。
- 畳み込みニューラルネットワークは、ある画像と、それを5度回転した画像とが同じ分類ができるかは確かではない。
- ほとんどの機械学習では、物体検出の回転不変性は組み込まれていない。
- 学習時のデータ拡張があるから十分ではないの?
- ええ、学習時のデータ拡張はそのための有用な手段です。
- そのため、たいがいの物体検出タスクでは、回転させるデータ拡張が用意されています。
- しかし、たいがいのフレームワークでは、元画像と回転後の画像とで同じ結果になるべきという束縛はない。
そのため、別な画像が1つ加わった程度の効果としかならない。
微小な変動に対するロバスト性を上げること
- 微小な変動に対するロバスト性をあげられば、機械学習の安定性が向上するのでないだろうか。
- 機械学習の重みの学習の前半は、画像からの特徴量抽出の意味あいが高い。
− だから、微小変度の有無に対して類似した特徴量抽出ができるようにすれば、学習のロバストさが向上するのではないだろうか。
画像の機械学習の画像の彩度が高い理由
-
機械学習処理では、内挿は簡単だが、外挿は難しい。
-
だから、入力として起こりうる範囲を網羅的にカバーするほうが、問題は単純になりやすい。
-
そのことを画像認識に当てはめると、機械学習の入力データのとりうる範囲を広めたほうがいい。
-
グレースケール画像をあたえるのならば、[0,255]の範囲になるように最小値と最大値をコントロールしてから入れたほうがいい。
-
このことは画像の彩度についても当てはまる。
彩度が低いデータだけを学習させたときには、彩度が高いデータに対してどのように推論をすればよいのかが与えられていなくなってしまう。