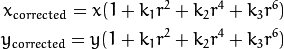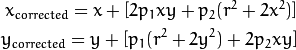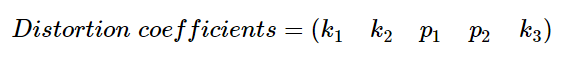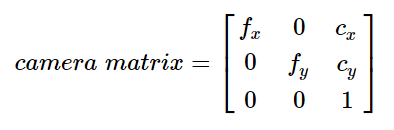以下の訳が鳥取大学内のサイトにあることがわかりました。
私のつたない訳は、必要性がなくなりました。
「OpenCV-Python Tutorials」 和訳の中の
Camera Calibration
の訳を作成しました。
3.1 での原文
つたない訳ですので、用語の訳や文の解釈に間違いが残っている可能性があります。
しっかりした理解のためには「詳解 OpenCV」
を読むことを強く推奨します。
原著は、その後OpenCV3に対応した版が出版されています。
Learning OpenCV 3 Computer Vision in C++ with the OpenCV Library
の和訳が早くでるとうれしいな。
訂正:circular gridに対して間違った訳を与えていました。円を並べた格子と訳しなおしました。(2016/5/7)
カメラ校正 Camera Calibration {#tutorial_py_calibration}
Goal
この節では
- カメラの歪み、カメラの内部パラメータ、外部パラメータなどについて学びます。
- これらのパラメータの求め方を学び、画像を歪み補正したりします。
Basics
今日の安価なピンホールカメラには、たくさんの歪みがあります。主な2つの歪みは
半径方向歪み、円周方向歪みです。
半径方向歪みのため、直線が曲がって見えます。その効果は、画像の中心から離れるほど大きくなります。1例として、1枚の画像を以下に示します。チェスボードの2つのエッジが赤い線で示されています。しかし、境界がまっすぐな線ではなく、赤い直線と一致していないことに気づくでしょう。期待される全ての直線は、外に向けて膨らんでいます。詳しくは、[歪曲収差]
(https://ja.wikipedia.org/wiki/%E6%AD%AA%E6%9B%B2%E5%8F%8E%E5%B7%AE)をたずねてください。
この歪み(訳注:半径方向歪み)は以下のように表されます。
同様に、もう一方の歪みは、円周方向歪みで、画像面に完璧に平行に取り付けられたわけではないレンズで撮られた写真で生じる歪みです。 そのため、画像の中のいくつかの領域は、期待されているよりも近づいて見えるかもしれません。その歪みは次のように表されます。
要するに、歪み係数として知られる以下の5つのパラメータを見つける必要があります(訳者注)。
訳者注:
2つの歪みがあるときの補正式は「詳解 OpenCV」p.399 に記載があります。
この他にも、ちょっとした情報を見つける必要があります。カメラの内部パラメータと外部パラメータです。内部パラメータは個々のカメラに固有のものです。焦点距離 (\f$f_x,f_y\f$)、光学中心 (\f$c_x, c_y\f$)などの情報を含んでいます。カメラ行列とも呼ばれています。内部パラメータは、カメラだけに依存しているので、いったん計算されれば、その後の利用のために保存しておくことができます。内部パラメータは、3x3行列で表されます。
外部パラメータは、ある3D点の座標を別の座標系に対応させる回転と移動ベクトルに対応します。
ステレオの用途のためには、まずこれらの歪みが補正されねばなりません。これらのパラメータ全てを見つけるためにしなければならないことは、1つのよく定義されたパターン(たとえばチェスボード)のたくさんのサンプル画像を提供することです。
それにある複数の特徴点(チェスボードの正方形のコーナー)をみつけます。それらの実空間の座標を知っており、画像中の座標を知っています。これらのデータを用いると、この歪み係数を得るためにある数学的な問題が背後で解かれます。それが全体像の要約です。よい結果を得るために少なくとも10枚のテストパターンが必要になります。
Code
上に述べたように、カメラ校正のためには少なくとも10枚のテストパターンを必要とします。
OpenCVには複数のチェスボード画像が付属しています。(samples/cpp/left01.jpg -- left14.jpg を参照のこと) そこで、それを用います。理解のために、たった1枚のチェスボードを考えます。カメラ校正に必要な重要な入力データは、3Dの実空間の点と対応する2Dの画像上の点からなる集合です。2Dの画像上の点は画像から容易に見つけ出すことができます。(これらの画像点は、チェスボード上で2つの黒い正方形が互いに接している場所です。)
訳者注:
$(opencv)\sources\samples\data
にleft01.jpg -- left14.jpgがあります。
実空間からの3D点はどうしましょう。これらの画像は固定したカメラから撮影されたものであり、チェスボードは異なる位置と向きで置かれている。 だから、(X,Y,Z)を知る必要があります。しかし、単純化のため、チェスボードはXY平面にあり(つまり 常にZ=0)、カメラの方が動いているとみなすことができます。この考察によって、X,Yの値だけ見つければよくなります。X,Yの値としては、(0,0), (1,0), (2,0),... といった流儀で複数の点を単に渡せばよくなります。この場合、私たちが得る結果は、チェスボードの正方形の大きさ(30mm)での縮尺での値になります。それで、(0,0), (30,0), (60,0),... といった値を渡すことででき、mmでの結果を受け取ります。(この例では、これらの画像を私たちがとっているわけではないので、正方形の大きさを知りません。だから正方形の大きさを単位として渡しています。)
3Dの点はオブジェクト点、2D画像上の点は画像点と呼ばれます。
Setup
チェスボードのパターンを見つけるために、
cv2.findChessboardCorners() 関数を用います。探しているのはどんな種類のパターンなのか、たとえば、8x8の格子なのか、5x5の格子なのかを渡す必要があります。
この例では、私たちは、7x6の格子を用います。(通常、チェスボードは8x8の正方形を持ち、7x7の内部のコーナーをもつ。) その関数は、複数のコーナー点と、パターンが検出されたときにTrueを返すretvalとを返す。
これらの複数のコーナーは、左から右、上から下への順序になっている。
@sa この関数は、全ての画像中の必要とされるパターンを見つけつくすことができないかもしれません。その場合のよい選択肢は、コードを書き、カメラを起動させ各フレームで必要なパターンをチェックさせることです。いったんパターンが得られると、コーナーを探してリストの中に保存します。次のフレームを読み取る前に間を空けます。それによってチェスボードを別な向きに調整することができるようにします。この過程をよいパターンが必要な数に達するまで続けます。ここにある例題においても、与えられた14を離れて考えたとき、何枚がよいのかが私たちは確信をもっていません。そこで、全ての画像を読み込んで、よいものとして扱っています。
@sa チェスボードの代わりに、円を並べた格子(circular grid)を使うことができます。そのときには、cv2.findCirclesGrid() をパターンを見つけるために使ってください。円を並べた格子を使うときには、少ない枚数で足りると言われています。
コーナーを見つけると、**cv2.cornerSubPix()**を用いてコーナーの精度をあげることができます。**cv2.drawChessboardCorners()**を用いてパターンを描画することができます。これらのステップの全ては、以下のコードに含まれています。
import numpy as np
import cv2
import glob
# termination criteria
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)
# Arrays to store object points and image points from all the images.
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.
images = glob.glob('*.jpg')
for fname in images:
img = cv2.imread(fname)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
# Find the chess board corners
ret, corners = cv2.findChessboardCorners(gray, (7,6),None)
# If found, add object points, image points (after refining them)
if ret == True:
objpoints.append(objp)
cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
imgpoints.append(corners)
# Draw and display the corners
cv2.drawChessboardCorners(img, (7,6), corners2,ret)
cv2.imshow('img',img)
cv2.waitKey(500)
cv2.destroyAllWindows()
パターンが書き込まれた1枚の画像を以下に示します。
校正(Calibration)
今では、オブジェクト点と画像点とを持っているので、校正の準備ができています。
校正のためには、 **cv2.calibrateCamera()**を使います。この関数は、カメラ行列、歪み係数、回転と並進ベクトルなどを返します。
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1],None,None)
歪み補正(Undistortion)
やろうとしていることが分かりました。さあ、写真をとって、その写真を歪み補正しましょう。OpenCVには2つの方法があります。以下に示します。でもその前に、**cv2.getOptimalNewCameraMatrix()**を使って free scaling parameter に基づいてカメラ行列を改善することができます。scaling parameter alpha=0 のときは、その関数は、歪み補正した画像をほしくない画素を最小限にしたやりかたで返します。そのため、画像の隅にあるいくつかの画素を除去するかもしれません。alpha=1のときには、全ての画素は保たれ、元データのない部分は黒い画像となります。その関数は画像のROIをも返し、結果を切り出すために用いることができます。
それでは、新しい画像を1枚とります(ここではleft12.jpgを使います。この章での最初の画像です)。
img = cv2.imread('left12.jpg')
h, w = img.shape[:2]
newcameramtx, roi=cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))
訳者注:left12.jpg は 以下のURLから入手できます。 https://github.com/rajatsaxena/OpenCV
1. **cv2.undistort()**の利用
これはてっとりばやい手順です。関数を呼び出して、その結果から上で得られたROIを用いて切り出します。
# undistort
dst = cv2.undistort(img, mtx, dist, None, newcameramtx)
# crop the image
x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite('calibresult.png',dst)
2. remapの利用
これは、まわりくどい手順です。
まず、歪み画像から歪み補正画像への写像関数を求めます。次にそのremap関数を利用します。
# undistort
mapx,mapy = cv2.initUndistortRectifyMap(mtx,dist,None,newcameramtx,(w,h),5)
dst = cv2.remap(img,mapx,mapy,cv2.INTER_LINEAR)
# crop the image
x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite('calibresult.png',dst)
両方の手法は同じ結果を与えます。以下の結果をご覧ください。
結果の画像では、全てのエッジがまっすぐであるのを見てとれます。
ここで、カメラ行列、歪み係数をNumpyの書き込み関数(np.savez, np.savetxt など)を使って、後での利用のために保存することができます。
再投影誤差(Re-projection Error)
再投影誤差は、見つかったパラメータがどれだけ正確かを示すよい評価方法です。その値が可能な限り0に近いほど望ましい。内部パラメータ、歪み、回転、並進行列が与えられたときに、まず**cv2.projectPoints()**を使ってオブジェクト点を画像点に変換する。その後、変換結果とコーナー検出アルゴリズム(の結果)との間の差のノルムを計算する。平均誤差を求めるために、校正画像の全てについて誤差の算術平均を計算する。
mean_error = 0
for i in xrange(len(objpoints)):
imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
tot_error += error
print "total error: ", mean_error/len(objpoints)
Additional Resources
訳者による追記
「超広角低歪なレンズの高次多項式モデルを用いたカメラキャリブレーション」
http://www.roboken.esys.tsukuba.ac.jp/~ohya/pdf/Robomech2014-KNS.pdf
Exercises
-# Try camera calibration with circular grid.
訳者による補足
OpenCV-Python Tutorialsの「カメラ校正」への補足
として別記事にいたしました。
OpenCV 2.4.0 のサンプルソースの一覧(samples/cpp)
https://github.com/YusukeSuzuki/opencv_sample_list_jp/blob/master/samples_cpp.rst
からC++でのステレオに関係するサンプルプログラムを読むのも有益です。
Tsaiのモデル
Tsai Camera Calibration
http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/DIAS1/
pyTsai - automated camera calibration in Python
https://github.com/Csega/pyTsai/blob/master/doc/index.rst