More than 5 years have passed since last update.

ABC-C第4弾

Last updated at 2018-10-05Posted at 2018-03-24

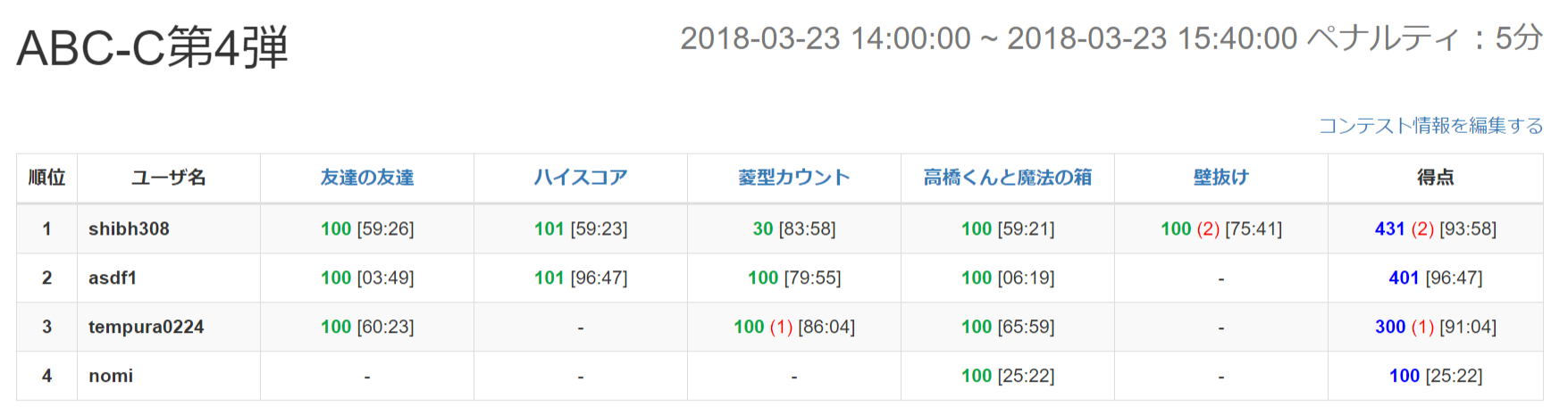
バチャでC問題を解く
1問しか解けなかった。悲しいね。

ABC016 「友達の友達」

解法1：自分でアルゴリズムを考える

最低条件を考えてみる

いきなりいろんなことを考えると頭が爆発する。
なので、まずはAさんとBさんが友達の友達になる最低条件を考える。
AさんとBさんが友達の友達になる最低条件は以下の2つを満たすときである。
1. AさんとBさんが友達でない
2. AさんとCさん、BさんとCさんがそれぞれ友達である

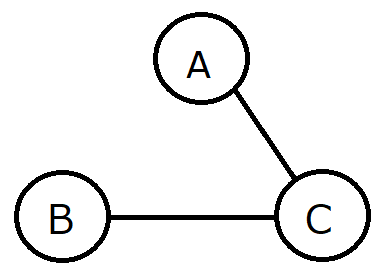
上の図では適当にCさんを仲介人として挙げたが、AさんとBさんの仲介となる人は誰でもいい。大事なのは、AさんとBさんが友達の友達であるかどうかである。なので、AさんBさんを固定して、それ以外の人を仲介として全探索する。

もしAさんとBさんを仲介する人が見つかり、かつAさんとBさんが友達でないならば、AさんとBさんは友達の友達となる。見つからなければ、AさんとBさんは友達の友達ではない。

全体的なことを考える

AさんとBさんが友達の友達かどうかを判定する方法はわかった。
次に、Aさんの友達の友達は何人になるかを考える。これは簡単で、AさんとBさんを固定して仲介を全探索すれば、AさんとBさんは友達の友達かどうかを判定できた。なので、次はAさんとCさんを固定して全探索すればAさんとCさんが友達かどうかを判定できる。次はAさんとDさんを固定して仲介を全探索。次はAさんとEさんを固定して仲介を全探索。
以上の探索で条件が当てはまる個数が、Aさんの友達の友達の人数になる。
B, C, D, Eさんの友達の友達は何人かを数える場合も同様の探索をすれば答えが求められる。

解法1のまとめ

AさんとBさんが友達の友達かを判定するには、AさんとBさんを固定して仲介する人を全て調べる。条件に当てはまる人が一人でもいればAさんとBさんは友達の友達となる。
Aさんの友達の友達の人数を求めるには、AさんとCさんを固定して仲介を全探索、AさんとDさんを固定して仲介を全探索...のように調べていく。条件に当てはまる人数がAさんの友達の友達の数となる。

コード

# include <bits/stdc++.h>
using namespace std;

int N, M;
int B[11][11];

int main() {
   // 入力 
   cin >> N >> M;
   for (int i = 0; i < M; i++) {
      int a, b;
      cin >> a >> b;
      a--, b--;
      B[a][b] = B[b][a] = 1;
   }

   // iとjは友達の友達か？kを仲介として調べる
   for (int i = 0; i < N; i++) {
      int cnt = 0; // iの友達の友達の人数
      for (int j = 0; j < N; j++) {
         bool exist = false; // iとjが友達の友達となる条件を満たすようなkがいるか？
         for (int k = 0; k < N; k++) {
            if (i == j || j == k || k == i) continue;
            if (B[i][k] && B[k][j] && !B[i][j]) exist = true;
         }
         if (exist) cnt++; // iとjが友達の友達ならカウントをインクリメント
      }
      cout << cnt << endl;
   }

   return 0;
}

解法2：最短経路アルゴリズムを使う

解法1と同様に、友達の友達となる条件を考える。
ここでは解法1よりもグラフっぽく考えてみる。

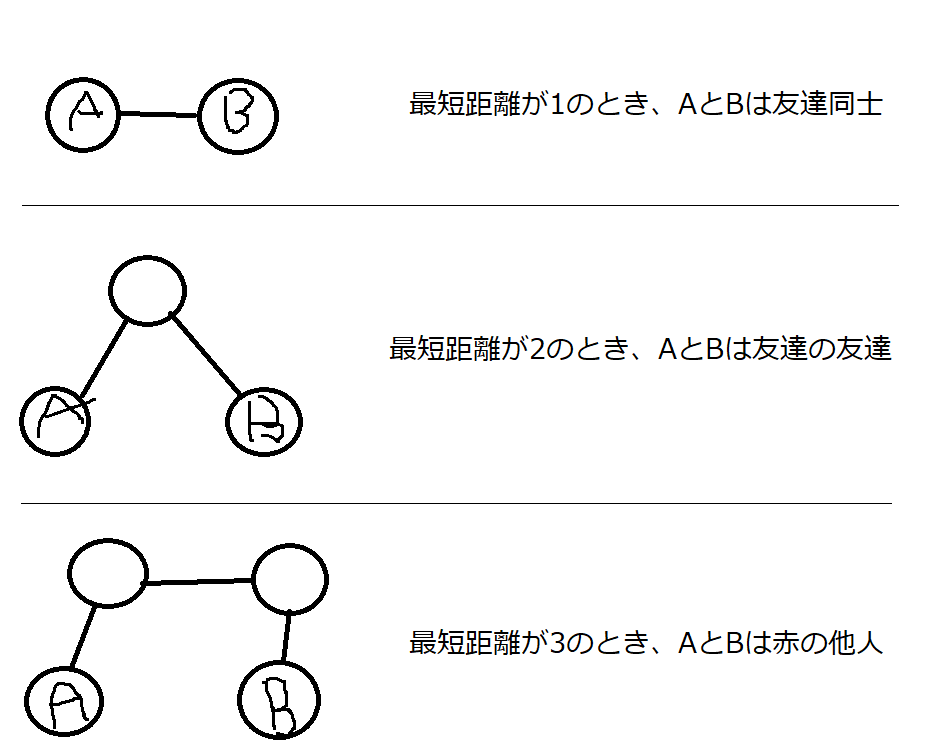
最短距離が1だと友達となる。
最短距離が3以上のときは赤の他人となる。
- 最短距離が3以上ということは、AにとってBは友達の友達の友達となるので赤の他人みたいなもの。
AとBが友達の友達となるには、AとBの最短距離が2であればいいことになる。
最短経路アルゴリズムにはワーシャルフロイド法をつかう。たぶん一番実装が楽

コード

# include <bits/stdc++.h>
using namespace std;

const int INF = 1e8;
int N, M;
int B[11][11];

int main() {
   // 初期化
   for (int i = 0; i < 11; i++) {
      for (int j = 0; j < 11; j++) {
         if (i == j) continue;
         B[i][j] = INF;
      }
   }

   // 入力
   cin >> N >> M;
   for (int i = 0; i < M ; i++) {
      int a, b;
      cin >> a >> b;
      a--, b--;
      B[a][b] = B[b][a] = 1;
   }

   // ワーシャルフロイド法
   for (int k = 0; k < N; k++) {
      for (int i = 0; i < N; i++) {
         for (int j = 0; j < N; j++) {
            B[i][j] = min(B[i][j], B[i][k] + B[k][j]);
         }
      }
   }

   for (int i = 0; i < N; i++) {
      int cnt = 0;
      for (int j = 0; j < N; j++) {
         if (i == j) continue;
         if (B[i][j] == 2) cnt++;
      }
      cout << cnt << endl;
   }

   return 0;
}

感想

解法1も2も自分で思いつける気がしない
友達の友達となる最低条件を定義することが大事だったように思う。
最低条件が分かれば、あとはそれを全体に適応させるというイメージ...?
この問題を見たときは一気にたくさんの処理をしないといけない気がして頭が爆発した。
でも、Aさんの友達の友達は何人か、Bさんの友達の友達は何人か、Cさんの(ryのように、1人1人友達の友達の人数を順番に求めていけば思考がスッキリする。
この問題を解くときに、なぜか仲介人を中心として考えてしまったため、内容が複雑に感じた。自分の中では1人1人について順番に考えていくというのが大事だったように思う。
実際に問題を解くときも、一気にいろんな事を考えずにできるだけ単純に考えられるようにしたい。

ABC017 「ハイスコア」

いきなり計算量の少ない解法を考えるのは難しいので3段階に分けて計算量を落としていく

第1段階：全探索

遺跡 $i(1\leq i \leq N)$ に訪れるか訪れないかを全通り試す。
例えば遺跡が3つある場合は以下のようになる。（o : 訪れる｜x : 訪れない）

遺跡1	遺跡2	遺跡3
x	x	x
x	x	o
x	o	x
x	o	o
o	x	x
o	x	o
o	o	x
o	o	o

このように、訪れるか訪れないかの組み合わせを全列挙するには2つ方法がある。
1つ目はビット全探索、2つ目は深さ優先探索である。
どちらも本質的な処理は同じなので好きな方で実装すると良いと思う。
計算量は$O(2^N\times N \times M)$ となる。

部分点コード(30点)

bit全探索のコード
深さ優先探索のコード
ちなみに、処理はほとんど同じなのにbit全探索のコードはWAになって深さ優先探索がTLEになるのには理由がある。それは、bit全探索のコード中にある$2^N$ において、$N$が大きいとオーバーフローを起こして値がおかしくなるからである。

第2段階：問題文を読み替える

これについては、頑張って思いつくしかないです。
問題文の「全ての宝石が揃ってはいけない」を「少なくとも取ってはいけない宝石が1種類ある」に読み替える。
つまり、取ってはいけない宝石の種類を1つ固定して、それを取らないような遺跡に訪れれば良い。
外のループで、絶対に取らない宝石の番号を固定する。中のループでは、取らないと決めた宝石を取らないような遺跡に訪れる。その結果、一番大きい値が答えとなる。
計算量は$O(MN)$ となる。
問題文を読み替えると解くのが劇的に簡単になる問題が割とあるので、問題文を読み替えて簡単にするという発想が大事なのかなーと思う。

部分点コード(100点)

部分点コード

第3段階：集合として考える

取ってはいけない宝石に注目するという点では第2段階と同じ方針でいく。
第2段階の方針の本質は、「宝石 $i$ を取らないような遺跡を訪れる」だった。
それを図にすると以下のようになる。黒い部分が求めたい部分となる。

外側の丸が全体となり、内部は宝石 i を取るものと宝石 i を取らないものに分かれている
この図を見ると気づきを得ることができる。
全体のスコアから宝石 i を取る遺跡に訪れたときに獲得するスコアを引くことで、宝石 i を取らない遺跡に訪れたときに獲得するスコアが求められるのでは？
つまり、第3段階の方針は「$全体-いらないデータ=欲しいデータ$を計算する」こととなる。
よって、求めるべきものは以下の2つとなる。
1. 全ての遺跡に訪れたときに獲得するスコア
2. 宝石iを取る遺跡に訪れたときに獲得するスコア
全ての遺跡に訪れたときに獲得するスコアは、入力で与えられるスコアを全て足し合わせれば求めることができる。
宝石 i を取る時のスコアは入力例1を例にとって考えてみる。図にすると以下のようになる

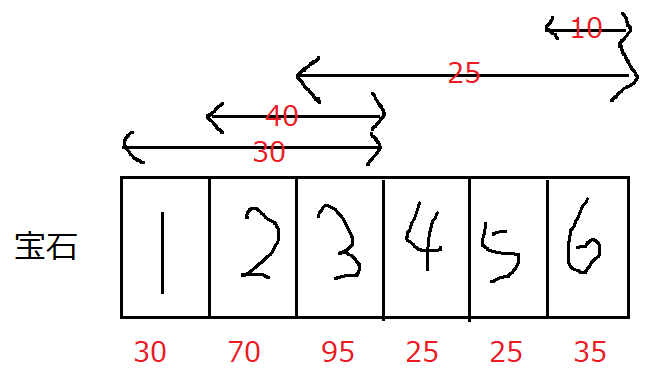
宝石1を取ると30点、宝石2を取ると70点、宝石3を取ると95点、宝石4を取ると25点、宝石5を取ると25点、宝石6を取ると35点となる。
つまり、宝石 i を取る時のスコアを表現する配列を作り、遺跡に訪れたときに獲得する宝石の範囲にスコアを足せば欲しいデータを得ることができる。
実装にはいもす法を使うが、ここでは説明しない。

ACコード

# include <bits/stdc++.h>
using namespace std;

const int MM = 111111; // Mの最大値。少し多めに取る
int N, M;
int imos[MM]; // いもす法を使うための配列

int main() {
   cin >> N >> M;
   long long sum = 0; // 全体の合計スコア
   for (int i = 0; i < N; i++) {
      int l, r, s;
      cin >> l >> r >> s;
      l--, r--;
      imos[l] += s, imos[r+1] -= s;
      sum += s;
   }

   for (int i = 1; i <= M; i++) {
      imos[i] += imos[i-1];
   }

   sort(imos, imos+M);
   // 全体 - 取ったときに一番スコアが少ない宝石
   cout << sum - imos[0] << endl;

   return 0;
}

感想

むっっっずうううううううううううううううううううううう。難しい。。。
全探索はかろうじて思いつくけど
問題文の「全ての宝石が揃ってはいけない」を「少なくとも取ってはいけない宝石が1種類ある」に読み替える部分、あれが無理だね。少なくとも1つだけって言う表現、中学数学とかでよく見かけた希ガス。
問題文の読み替え、苦手なんだよなー。
でも問題文を読み替えることで難易度が激減する問題が結構あったりするからな－。
ということで、この問題で大事だったのは問題文の読み替えだった。
取ってはいけない宝石を固定するっていうのも大事だよねー、多分。
計算量を落とすときは値を固定するっていう考えをよく使う気がする。
つまり、固定できそうな値をひとつみければ計算量が落ちるのでは？？？？？とか思ったり
あと、図を書くと方針がつかめることがよくある気がする。
今回の場合、「全体」の集合を書いて、その中を「宝石iを取る」「宝石iを取らない」に分けた。
ベン図を書くと問題文中の値とかを綺麗に分けて考えられるからいいと思う。たぶん。
こんだけ長々と説明しないと自分で理解できないのでとても悲しいね。みんななんでこんな問題解けるんだ？たぶん異星人の血とか混ざってて強いんだと思う。

ABC018 「菱型カウント」

いきなり計算量が少ない解法を考えるのは難しいので、2段階に分けて計算量を落とす

第1段階：全探索

以下の操作を全てのマスについて行う
1. 1つのマスを菱形の中央とする。
2. 中央からのマンハッタン距離$K-1$以内が全てoであればそのマスを中心とした菱形が作れる。
計算量は$O(RCK^2)$ となる。

部分点コード(30点)

部分点コード

第2段階：

考察の流れ

全てのマスを見るという操作は外せそうにない。これを外すと処理が面倒になりそう(直感)
なので、菱形を素早く判定する方法を考える。
$K \times K$のマス目を全て見なくても菱形だと判定するにはどうすれば...？
菱形判定を$O(K^2)$ から計算量を減らすには、$O(K)$くらいが妥当かなー？
菱形、横から見るか？縦から見るか？
突然ですが、ここである考え方を使います。それは、データ列が現れたときはとりあえず累積和を取ってみるというものです。計算量を落とす考察に行き詰まったらとりあえず累積和を取ります。自分もこの考え方に何度か救われました。
とりあえずoを$1$、xを$0$とした整数型の配列を作ります。
2次元座標だから2次元累積和を取ろうか？でも菱形は正方形じゃないから扱いにくそう
1次元の累積和を考えてみよう。こんな感じでいろいろ実験してみる。
ここで、縦に連続した値が大事そうだということに気がつく。この値を見れば、上にどれだけoがあるのかを$O(1)$で求めることができる。なんかこれ使えそうじゃない？
菱形の列を左から走査する。そのとき菱形の底の値を見て、全ての底の値が菱形が作れそうな値になっていたら菱形を作ることができる。このとき見るのは$K$個だけなので、計算量が一つ落とせた！やったぜ！
考察終了！

解法

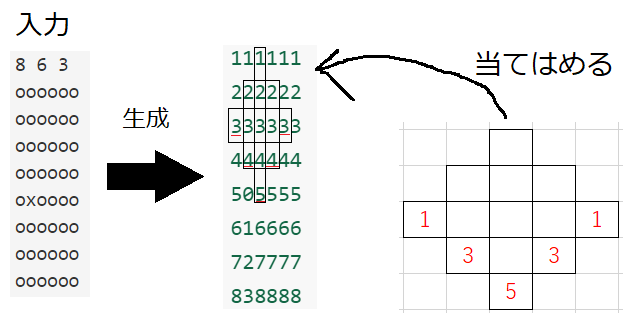
与えられた長方形を縦に見て、連続したマスをカウントする。
例えば、入力例3が与えられたとき、縦に連続してカウントした長方形は上の図のようになる。
そして、マス目に対して菱形を当てはめる。そして、当てはめた場所と対応する赤い数字を見る
見ているマスについて、菱形の底の数字が全てが赤い数字以上なら菱形をつくることができる。
全体的な計算量は$O(RCK)$ となる。
- 部分点解法では全てのマスについて$K\times K$個の菱形全体をみた。
- 満点解法では菱形の底の数字だけを見た。これは菱形の横の長さなので$K$個だけをみたことなる。
- なので、部分点解法の計算量の$K$が1つ落とせた。

ACコード

# include <bits/stdc++.h>
using namespace std;

int R, C, K;
int A[555][555];

bool check(int y, int x) {
   for (int i = -K; i <= K; i++) {
      int num = K - abs(i); // yからnumだけ座標が下がる
      int nx = x + i, ny = y + num; // nx, nyが赤い数字の座標となる
      if (nx < 0 || nx >= C || ny < 0 || ny >= R) return false; // 範囲外ならfalse
      int need = num * 2 + 1; // 縦に見た、必要な菱形の長さ
      if (A[ny][nx] < need) return false; // 底の値が必要な値に達していないならfalse
   }

   return true;
}

int main() {
   cin >> R >> C >> K;
   K--; // デクリメントした方が都合が良い
   for (int i = 0; i < R; i++) {
      for (int j = 0; j < C; j++) {
         char b;
         cin >> b;
         A[i][j] = b == 'o';
      }
   }

   // 縦の連続したマスについて累積和
   for (int i = 0; i < C; i++) {
      for (int j = 1; j < R; j++) {
         if (!A[j][i]) continue;
         A[j][i] += A[j-1][i];
      }
   }

   int ans = 0;
   // 全てのマスについて調べる
   for (int i = 0; i < R; i++) {
      for (int j = 1; j < C; j++) {
         if (check(i, j)) {
            ans++;
         }
      }
   }
   cout << ans << endl;

   return 0;
}

感想

自分が思いつくとしたらこんな感じだろうって感じで考察書いたけど、こんなん普通思いつかなくね？
しかも、実装めっちゃバグるし。こんなの時間内に通せねーよ、といった感じ。
$R, C, K$ の最大値はそれぞれ$500$だから$RCK_{MAX}=1.25\times 10^8$ になるんだが、計算量ギリッギリじゃね？
どうやらBFSで解くと、さらに計算量が落とせるみたい。わからないので誰か記事書いて！

ABC019 「高橋くんと魔法の箱」

考察

$x$ を入れたときと$2x$ を入れたときに出てくる整数は同じである。
つまり、$x$と$2x$ は仲間である。
$x$の仲間は他にいないだろうか？という事を考える。

$$
x ⇔ 2x \
x'=2x とする。\
x'⇔2x'\
展開すると \
2x⇔4xとなる。\
繋げると\
x⇔2x⇔4xになる。
$$

これを繰り返していくと、$x, 2x, 4x, 8x, 16x,..$ のようになることがわかる。
つまり、$x$と、$2^{n}x$ は同じグループとなる。
入力された値を$2$で割り切れなくなるまで割った数字をそのグループの代表の数字とする。
その数字の種類が答えとなる。
具体的な数字で考えると以下のようになる

コード

# include <bits/stdc++.h>
using namespace std;

int get(int x) {
   while (x % 2 == 0) {
      x /= 2;
   }
   return x;
}

int main() {
   int n;
   cin >> n;
   set<int> s;
   for (int i = 0; i < n; i++) {
      int x;
      cin >> x;
      s.insert(get(x));
   }
   cout << s.size() << endl;

   return 0;
}

感想

この問題で大事だったのはグループ分けの法則がつかめるかどうか？だと思う。
難しくね？この問題。毎回言ってるけど
$x, 2x,4x, 8x, ..$が仲間だと見抜けなければおしまい。
自分で解説書いたけど、自力で解ける気がしない。
にゃーん

ABC020 「壁抜け」

考察

どうすれば最大の $x$ を求める事ができるのかを考える。
深さ優先探索で$x$の個数が少なくなるような進み方をする...?でもそれが最適とは言い切れない
そもそもどういう進み方をするのが最適なのかわからない。進み方の組み合わせが多すぎて頭が爆発する
良い感じの探索をする方法を思いつけそうにない。だったらシミュレーションすれば良い。
$x$ を自分で決めて、実際にゴールまでの最小コストを求めれば良い。ゴールまでの最小コストは最短路アルゴリズムとか使えば簡単に求められそう。$x$について$1$からループを回して、最小コストが$T$以下になる最大の$x$が答えとなる。
しかしここで問題が発生する。$x$ の値の範囲は$1\leq x \leq 10^9$ であるため、$x$を線形探索していては計算量が多すぎて答えが出るのに時間がかかる。
そこで、2分探索の出番である。2分探索は値が連続する区間において任意の値を見つけるのが得意だ。
2分探索を使えば$x$を探索する計算量は$O(log{T})$ になる。線形探索が$O(T) $ なのに比べて劇的によくなった。
この考察、考えた事をそのまま書き出しただけなので読みにくいかもしれません。

解法

以下の2つの操作を繰り返していけば最大の$x$の値を求めることができる。

$x$の値を決め打つ。
- $x$の値は2分探索によって定める。
スタートからゴールまでの最小コストを求める。操作1に戻る。
- 最小コストは最短路アルゴリズムなどで求める。(僕はダイクストラ法を使いました)
- コストが$T$以下になるか、$T$より大きくなるかに応じて2分探索の範囲を適切に狭める。

実装方法

最短路アルゴリズムの実装でちょっと詰まったのでメモしておく
結論から言うと、ダイクストラ法で解くのが安全ということになった。

メモ化再帰

僕にとって最短路はメモ化再帰で求めるのが一番楽でアルゴリズム的にも効率的だと思っていた。なので初めはメモ化再帰で実装した。
でも、メモ化再帰で最短路を求めるのは少し危険である。なぜなら、値の書き換えが何度も発生する可能性があるからである。
毎回値の書き換えが起こった場合、計算量は$O(4^{HW})$ となるので、間に合わない。
でも、意地悪なテストケースがなかったからこの問題はメモ化再帰でACできた。

コード

メモ化再帰での実装例

幅優先探索

最短路をお手軽に求めるならBFSでしょって感じのアルゴリズム。
計算量が$O(HW)$ なのが魅力的
でも、実装でちょっとバグりそうなので止めた
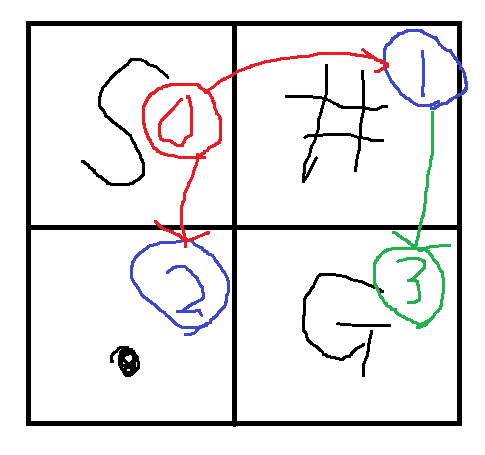
#が10のとき、以下の画像だと最短距離は11になってしまう。
BFSは1手目、2手目、3手目...のように埋めていくアルゴリズムなので、探索順序によっては不都合が発生する。
多分工夫すればBFSで解けるけど、できることなら工夫せずに何も考えずに解きたい。

最短路アルゴリズム

というわけで、おとなしく最短路アルゴリズムを使うことにする。
そっちの方が何も考えずに解けそう。
計算量が少ないダイクストラ法を使う。

ダイクストラ法の手順

キューから頂点を取り出す
取り出した頂点に隣接するマスを調べる。

蟻本に載ってるダイクストラの手順2は、取り出した頂点に隣接する頂点を調べるものとなっている。この問題では、隣接する頂点の代わりに隣接するマスを調べている。

2分探索+ダイクストラ法で解いたコード

# include <bits/stdc++.h>
using namespace std;

using ll = long long;

// 座標(y, x)を管理
struct P { ll y, x; };

// (最短距離, 座標)の情報
struct V { 
   ll dist; 
   P pos;
   // デフォルト
   bool operator>(const V &t) const {
      return dist > t.dist;
   }
   // greater
   bool operator<(const V &t) const {
      return dist < t.dist;
   }
};

const int dy[] = {0, 0, -1, 1};
const int dx[] = {1, -1, 0, 0};

const ll MAX = 1e9;
const ll INF = 1e15;
int H, W; // 高さ、幅
ll T; // 制限時間
int sy, sx, gy, gx; // スタート座標、ゴール座標
char B[50][50]; // 盤面の文字の情報
ll dist[50][50]; // 盤面の距離の情報

// ダイクストラ法で距離を求める。cは'#'のコスト
ll dijkstra(ll c) {
   for (int i = 0; i < H; i++) for (int j = 0; j < W; j++) dist[i][j] = INF;
   dist[sy][sx] = 0;
   priority_queue<V, vector<V>, greater<V>> Q;
   Q.push({0, P{sy, sx}});

   while (Q.size()) {
      V v = Q.top(); Q.pop();
      int y = v.pos.y, x = v.pos.x;
      // 隣接頂点を調べる代わりに隣接マスを調べる
      for (int i = 0; i < 4; i++) {
         int ny = y + dy[i], nx = x + dx[i];
         if (ny < 0 || ny >= H || nx < 0 || nx >= W) continue;
         ll cost = B[ny][nx]=='.' ? 1LL : c;
         if (dist[ny][nx] > dist[y][x] + cost) {
            dist[ny][nx] = dist[y][x] + cost;
            Q.push( V{dist[ny][nx], P{ny, nx}} );
         }
      }
   }
}

// 2分探索でxを決め打つ
ll bin() {
   auto check = [&](ll x) -> bool {
      dijkstra(x); // ダイクストラで距離を計算
      return dist[gy][gx] <= T;
   };

   // [l, r)の半開区間
   ll l = 1, r = T+1;
   while (r - l > 1) {
      ll m = (l + r) / 2;
      if (check(m)) {
         l = m;
      } else {
         r = m;
      }
   }

   return l;
}

int main() {
   // 入力
   cin >> H >> W >> T;
   for (int i = 0; i < H; i++) {
      for (int j = 0; j < W; j++) {
         cin >> B[i][j];
         if (B[i][j] == 'S') {
            sy = i, sx = j;
            B[i][j] = '.';
         }
         if (B[i][j] == 'G') {
            gy = i, gx = j;
            B[i][j] = '.';
         }
      }
   }

   // 処理はbin関数に丸投げ
   cout << bin() << endl;

   return 0;
}

感想

値を決め打って探索するという発想がなかった。この発想が結構大事そう
今まで解いた問題でも、2分探索で値を決め打ってから処理する感じの問題があった気がする。
でもなかなか2分探索で解くって気がつかないなー。。。
ダイクストラ法は、実際にグラフを作って解くものだと思っていた。しかし、グラフを作らなくてもダイクストラ法を使うことができるとわかった。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up