考察
- 直感的にはbはAの平均値。計算してみるがサンプルと合わない。平均値は違う
- bは真ん中あたりを取りたい気持ちなので、b=Aの中央値というパターンも考えてみる。サンプルと合わない。中央値も違う
- 問題文を式にすると$\sum_{i=1}^{N}|A_i - (b - i)|$となる。この式を見ても特に何も思いつかない
- 式変形すると、$\sum_{i=1}^{N}|(A_i - i) -b|$となる。わかりやすさのため$B_i = A_i - i$とすると式は$\sum_{i=1}^{N}|B_i -b|$となる。これは地点bから地点$B_i$までの距離の総和という意味になる。意味のある式になって嬉しい気持ち。
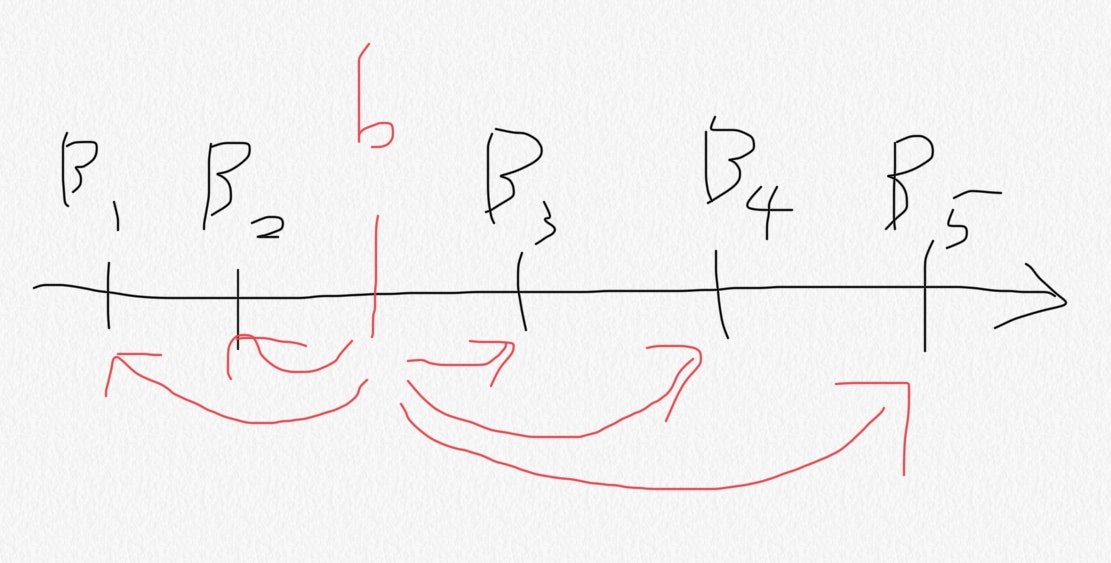
- よって、この問題は「地点bからN個の点の間のマンハッタン距離の総和を最小化する」という問題に帰着できる。図にするとこんな感じ。bから各$B_i$への距離を求める問題になる。
- マンハッタン距離の総和を最小化するときは、中央値を使うという典型がある。よってbは数列Bの中央値であれば良い。
お気持ちの証明
- マンハッタン距離の総和を最小化するときは中央値を使うといいってやつの証明
- N=5の場合を考える。
- 中央値からεずらすと、合計で-2ε + 3ε=εとなる。中央値からずらすとεだけ損害が出ることがわかるので、中央値からずらすべきではない。
- また、bが適当な位置にあった時、中央値に向かってずらすことを考える。すると、距離の合計は-4εされる。なので、中央に向かうと嬉しいことがわかる。
- 他の地点でも実験すると中央値を使うのがなんとなく正しいのがわかる。なんとなく。

コード
# include <bits/stdc++.h>
using namespace std;
# define int long long
int N;
vector<int> A, B;
int calc(int b) {
int ret = 0;
for (int i = 1; i <= N; i++) {
ret += abs(A[i-1] - (b + i));
}
return ret;
}
signed main() {
cin >> N;
A.resize(N);
B.resize(N);
for (int i = 0; i < N; i++) {
cin >> A[i];
B[i] = A[i] - (i + 1);
}
sort(B.begin(), B.end());
cout << calc(B[N/2]) << endl;
return 0;
}
要点
- マンハッタン距離の差の総和を最小化するときは中央値を使う(典型らしい)
メモ
- はまやんさんの記事。マンハッタン距離の差の総和を最小化するときは中央値という典型
- 競技プログラミングにおけるマンハッタン距離問題まとめ。類題載ってる。
- やまかささんの記事
- お気持ちの証明はわかった。でもちゃんとした証明は書けない。えーん
- iPhoneは図を描くためのツールではない