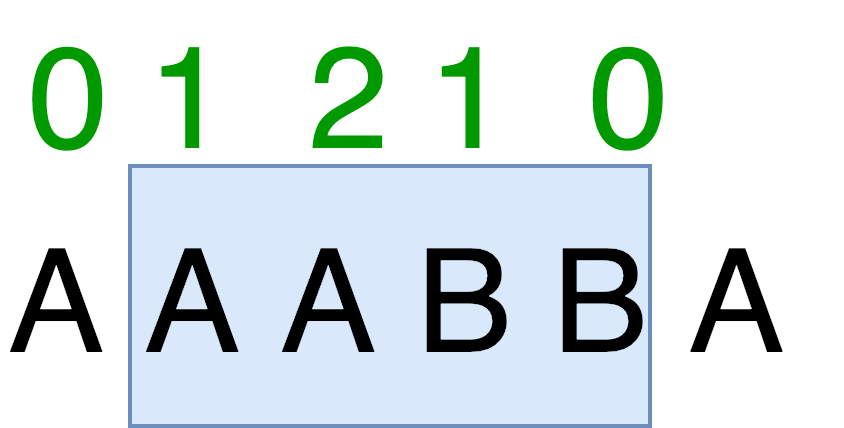
解いてる時の考察
- いい方法が何も思いつかないのでとりあえず愚直解を書いてみる
- ただ、愚直解は$O(N^2)$なので間に合わない。どうしよー
- DPかな?
dp[左端のインデックス][右端のインデックス]みたいな。いや、普通に遷移とか無理そう。そもそも配列作るときにdp[200001][200001]になってメモリが死ぬ。 - 配列を2つ用意して、AとBが出てきた場所を1にして累積和を取ると嬉しいことがありそう。ある区間にあるAの数が$O(1)$で求められるし。
- 以下のような配列を使っていい感じに処理すれば解けそう
A A A B B A // 文字列
1 2 3 3 3 4 // Aが出てきた回数
0 0 0 1 2 2 // Bが出てきた回数
- そんな感じの方針で提出したコードその1、その2。どっちも間違えてた。なんで間違えてるかはわかったけど、他にいい方法が思いつかない
- しゃくとり法も考えた。連続する数列といえばしゃくとり法なので。さらに、累積和をとった配列は単調増加なのでしゃくとり法で解いてくださいっていってるようなもんじゃん!!やったぜ!!
- と思ったけど、全然わからない。色々考えるけど穴がたくさん見つかるしもうダメ
- もうなにもわからない。
- 終了
理想の考察
- 愚直に計算すると$O(N^2)$で間に合わない。
- テストケース1の文字列で実験してみる。
AAABA中のAABBについて考える。文字列中にAが出てきたら+1、Bが出てきたら-1して累積和を取ると、以下の図のようになる。ある区間でAとBの数が同じなら、その区間の累積和は0になるということ。これが解くのに使えそう。
- サンプル1の累積和をとった図を描くと以下のようになる。数字が同じになる部分に注目する。数字が同じ部分はグラフの高さが同じになっている。これは、同じ数字で囲まれた区間ではAとBが出てきた回数が同じということを表す。区間の開始地点をX、終了地点をYとすると、AとBの数が同じになる区間は$(X, Y]$の半開区間となる。求める区間は長いほうがいいので数字が出てくる最初の地点を連想配列に突っ込めば解けそう。考察終了!

解法
- 累積和を取る用の配列を用意する。文字列中にAが出てきたら+1、Bが出てきたら-1しする。そのあと、配列の累積和を取る。
- ループを回し、右側を固定する。左側に今まで出てきた数があれば答えを更新する。なければ連想配列に値とインデックスを記録する。
(解法、言葉で説明するの難しいからコード読んだほうが早そう)
コード
# include <bits/stdc++.h>
using namespace std;
# define int long long
string s;
vector<int> rui;
map<int, int> mp;
signed main() {
cin >> s;
int n = s.size();
rui.resize(n+1);
// 文字列中にAがあったら+1, Bがあったら-1する
for (int i = 0; i < n; i++) {
if (s[i] == 'A') {
rui[i+1] = 1;
} else {
rui[i+1] = -1;
}
}
// 累積和を取る
for (int i = 1; i <= n; i++) {
rui[i] += rui[i-1];
}
int ans = 0;
for (int i = 0; i <= n; i++) {
// 前にrui[i]がmapに登録されてたら、答えを更新する
if (mp.count(rui[i]) != 0) {
ans = max(ans, i - mp[rui[i]]);
}
// 初めて出てきた数字ならmapに記録する
if (mp.count(rui[i]) == 0) {
mp[rui[i]] = i;
}
}
cout << ans << endl;
return 0;
}
要点
- ある区間に出てくるもののバランスを保つ問題では、ジグザグの図を考えると良い
- 今回の場合、Aなら+1、Bなら-1して累積和を取ることでジグザグの図ができた。
メモ
- 自力ACできなかった。
- Aが出てきたら+1、Bが出てきたら-1すると法則性が見えてくる。
- 記録する配列を1-indexedにしてなかったからちょっと詰まった。
- Aが出てきたら+1、Bが出てきたら−1、そんで累積和をとるっていう発想が必要だった。累積和、やっぱ1-idxのほうがいい。
- ジグザグは典型らしい
- satanicさんに教えてもらった問題で使った気がする
- かっこを対応させる問題と似た感じの考え方(以下は見てないので類題かは知らない)