- まちがってたらごめんね。変なところあったら指摘してね。
木の直径とは
- 木における最大頂点間距離のこと
double-sweepで求める
アルゴリズム
- 木として$T=(V, E)$が与えられる
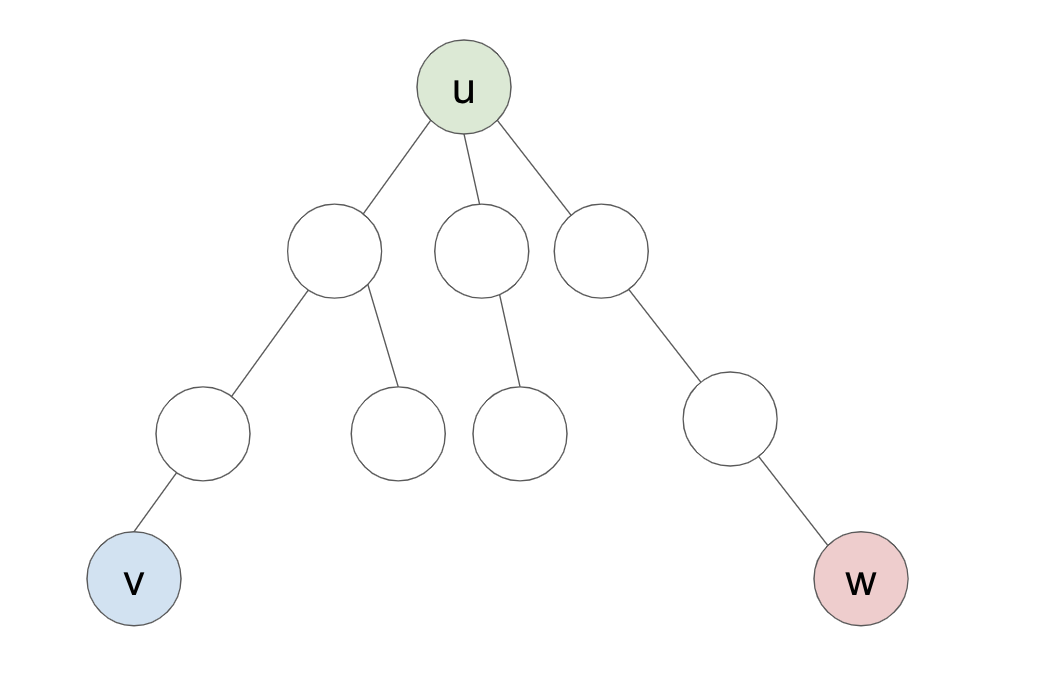
- ある頂点$u \in V$を選び、$u$を始点として最大距離となる終点$v \in V$を探し出す。
- 先ほど探し出した頂点$v$を始点として最大距離となる終点$w \in V$を探し出す。
- このとき、経路$v, w$の距離は木の直径となる。
証明
-
経路$v, w$が木での最長の経路となることを証明する。証明には背理法を使う。
-
経路$v, w$が木の最長経路とならないと仮定する。つまり、経路$v, w$より長い経路$a, b \in V$が存在すると仮定する。
-
木は頂点$a, b$の場所で大きく2通りに場合分けできる。
-
1つ目は$L = LCA(a, b)$が経路$u, v$上にあるときである。この場合を細かく(i), (ii)に分けて考える(図を参照)。
-
(i)について考える。以下の式より、$|ab|$以上となる$|vb|$が存在する。よって、この場合経路$a, b$は最長の経路ではない
|ab| = |aL| + |bL| \\
|aL| \leq |vL| \\
|ab| = |aL| + |bL| \leq |vL| + |bL| = |vb|
- (ii)について考える。(i)と同様に以下の式より、$|ab|$以上となる$|vb|$が存在する。よって、この場合経路$a, b$は最長の経路ではない
|ab| = |aL| + |bL| \\
|aL| \leq |vL| \\
|ab| = |aL| + |bL| \leq |vL| + |bL| = |vb|

- 2つ目は$L$が経路$u, v$上にないときである。これを細かくして(iii), (iiii)に分けて考える。
- (iii)について考える。$L_2=LCA(v, L)$とする。以下の式より、$ab$以上となる長さ$vb$が存在する。よって、この場合経路$a, b$は最長の経路ではない
|vL_2| \geq |aL_2| \\
|vL_2| > |aL| \\
|vL| > |aL| \\
|ab| = |aL| + |bL| < |vL| + |bL| = |vb|
- (iiii)について考える。以下の式より、以下の式より、$ab$以上となる長さ$vb$が存在する。よって、この場合経路$a, b$は最長の経路ではない
|uv| \geq |ua| \\
|uv| > |aL| \\
|vL| > |aL| \\
|ab| = |aL| + |bL| < |vL| + |bL| = |vb|

- はじめに経路$a, b$が最長の経路となると仮定した。しかし、(i)~(iiii)より、経路$a, b$が最長の経路ではないと証明した。経路$v, w$より長い経路$a, b$が存在するという仮定に矛盾が生じた。よって、木の直径は経路$v, w$の長さとなる。
コード
-
getTreeDiameter()を呼べば木の直径とその始点、終点が1通り求められる。
const int maxV = 111111;
vector<int> G[maxV]; // 頂点情報のみのグラフ
// treeDFS(親, 現在地, 根から現在地までの距離, 根からの最大の距離, 根から最大の距離となる頂点
void treeDFS(int from, int current, int dist, int &maxDist, int &maxVertex) {
// 距離と終点を更新
if (dist > maxDist) {
maxDist = dist;
maxVertex = current;
}
for (auto to : G[current]) {
// 逆流を防ぐ
if (to == from) continue;
treeDFS(current, to, dist + 1, maxDist, maxVertex);
}
}
void getTreeDiameter() {
int start = 0, end = 0, maxDist = 0;
treeDFS(-1, start, 0, maxDist, end);
start = end, end = 0, maxDist = 0;
treeDFS(-1, start, 0, maxDist, end);
printf("start: %d, end: %d, diameter: %d\n", start, end, maxDist);
}
直径を使って解く問題
メモ
- 直径は木DPでも求められるみたいなんだけど、木DPよくわからん。この辺の記事が良さげ。全方位木DPってやつらしい。
- double-sweepってアルゴリズム、ABC019のスライドに載ってたけどググっても出てこない。double-sweepは俗称みたいなもの?
- wからxへの最大の経路を$|wx|$とする。$|vw| \leq |wx|$だから$|vw|$が最大にならないのでは?と思ったけどそんなことはなかった。$a, b$は任意の頂点を表すので、$|ab|$が最大でないことを示せば$|vw|$が最大ということになった。
- 直径を使って解く問題、他にあったら教えてほしいです