コンテスト中の考察
- AとBを降順にソートした配列を持っておく(
pair<値, インデックス>の配列)。それと、どのインデックスを使ったかという情報も持っておく。高橋くんの手番の時はAを初めから取っていき、青木くんの手番の時はBを初めから取っていく。すでに使用したインデックスかどうかも判定する。この方法でコード書いたらWAでした。 - Aをとる時、同じ値が複数あるならBの値が大きい方を取るという方針も立ててみた。Aは常に最大を取り、ついでにBが大きい値をとるのを防ごうという作戦。でもこれも失敗。
- DPかな?状態の持ち方とか遷移思いつかないし無理っぽい
- 終了
理想の考察
- AとBを降順にソートして処理するとか、テキトーな貪欲は思いつくけど核心に迫るような考察が出てこない。
- 何も思いつかないときは小さいケースで実験してみる
- N=2の時を考える。このとき、「$A_1, B_1$」と「$A_2, B_2$」がある。
- まずは「高橋くんが獲得するポイントの総和 - 青木くんが獲得するポイントの総和」を最大化することを考える。仮に皿$1$を取るのが最善だとすると、$A_1 - B_2 \geq A_2 - B_1$という式が立てられる。この式を満たす時、皿1を取った方がお得になる。この式はこのままでは扱いづらいので、$A_1 + B_1 \geq A_2 + B_2$という式に変換する。すると、左辺と右辺でインデックスが独立するので、少し考えやすくなる。これで、$A_1 + B_1$が大きい方を取れば得点を最大化できるのでは?という仮説が立つ。
- 次に、「青木くんが獲得するポイントの総和 - 高橋くんが獲得するポイントの総和」を最大化することを考える。これは先ほどと同じように考えれば良い。仮に皿1を取るのが最善だとすると、$B_1 - A_2 \geq B_2 - A_1$という式が立てられる。先ほどと同様に式変形すると、$A_1 + B_1 \geq A_2 + B_2$となる。これは先ほどの「高橋くんが獲得するポイントの総和 - 青木くんが獲得するポイントの総和」を最大化するときと同じ式である。つまり、両者ともに$A_1 + B_1$が大きい方を取るのが最善手であるという仮説が立つ。
- ここまでで、両者ともに$A_i + B_i$が大きい方を取るのが最善手なのでは?というところまでたどり着く
- N=2で試したけど、N=3, N=4, N=5, ... で試したら別の法則性が出てきてさっき立てた仮説がひっくり返るかもしれない。でも、反例は特に思いつかないのでとりあえず仮説は正しそう(本当に正しいかどうかは別として確証を持てる)
- この考え方でコード書いて投げたらAC
解法
- A+Bの和とそのインデックスを持たせた配列Cを作る
- 配列Cを「A+Bの和」基準で降順にソートする
- 配列Cを先頭から見ていって、高橋くんと青木くんが交互に皿を取っていく
- 高橋くんの得点 - 青木くんの得点を出力する
コード
# include <bits/stdc++.h>
using namespace std;
# define int long long
using pii = pair<int, int>;
int N;
vector<int> A, B;
vector<pii> C; // {A_i + B_i, インデックス}
signed main() {
cin >> N;
A.resize(N);
B.resize(N);
for (int i = 0; i < N; i++) {
cin >> A[i] >> B[i];
C.push_back({A[i] + B[i], i});
}
sort(C.begin(), C.end());
reverse(C.begin(), C.end());
int tSum = 0, aSum = 0;
for (int i = 0; i < N; i++) {
int index = C[i].second;
if (i % 2 == 0) {
tSum += A[index];
} else {
aSum += B[index];
}
}
cout << tSum - aSum << endl;
return 0;
}
証明
- 本番中は必要ないけど一応証明っぽいものを考える
- N=2の実験で導いた$A_i + B_i$が大きい方を取ればいいんじゃね?っていう仮説をもとに「高橋くんのポイントの総和 - 青木くんのポイントの総和」を最大化することを考える。
- 高橋君が取った皿の集合をX、青木君が取った皿の集合をYとする。
- $\sum_{i \in X}^{}A_i - \sum_{i \in Y} B_i$を求めたい
- $A_i + B_i$がまとまった形で式に出てきてほしいという気持ちを込めながら天才になる。すると、$\sum_{i \in X}{} B_i - \sum_{i \in X} B_i$を足せばいいという発想になる(足しても計算結果は同じなので大丈夫)。これをすると、$\sum_{i \in X}^{}A_i$と$\sum_{i \in X}{} B_i $が結合できて嬉しい。
- あとは式変形していく(マークダウンで真面目に数式書くのだるいからイコールの記号とか使ってない)
- $\sum_{i \in X} A_i - \sum_{i \in Y}B_i + (\sum_{i \in X}B_i - \sum_{i \in X}B_i)$
- $\sum_{i \in X}(A_i + B_i) - (\sum_{i \in Y}B_i + \sum_{i \in X}B_i)$
- $\sum_{i \in X}(A_i + B_i) - \sum_{i=0}^{N-1}B_i$
- 式変形完了。この式を最大化したい。
- $\sum_{i=0}^{N-1}B_i$は定数なので考えない。
- $\sum_{i \in X}(A_i + B_i)$をみる。この式の値を大きくしたいので、$A_i + B_i$は大きい方が良い。なので、$A_i + B_i$を降順にソートして先頭から取っていくのが最善手だとわかる
- 「青木くんのポイントの総和 - 高橋くんのポイントの総和」も同様に考えることができる
その他の考え方(追記)
違うゲームとして考える
- 高橋くんが1~Nまでの皿を全て独占した状況を考える。高橋くんは自分が独占した皿の中から1枚守ることができる。青木くんは高橋くんの皿の中から1枚取り上げて自分のものにすることができる。
- このゲームについて考える
高橋くんの最善手は?
- 高橋くんは自分が持ってる皿の中で最もお得な皿を1枚死守する。
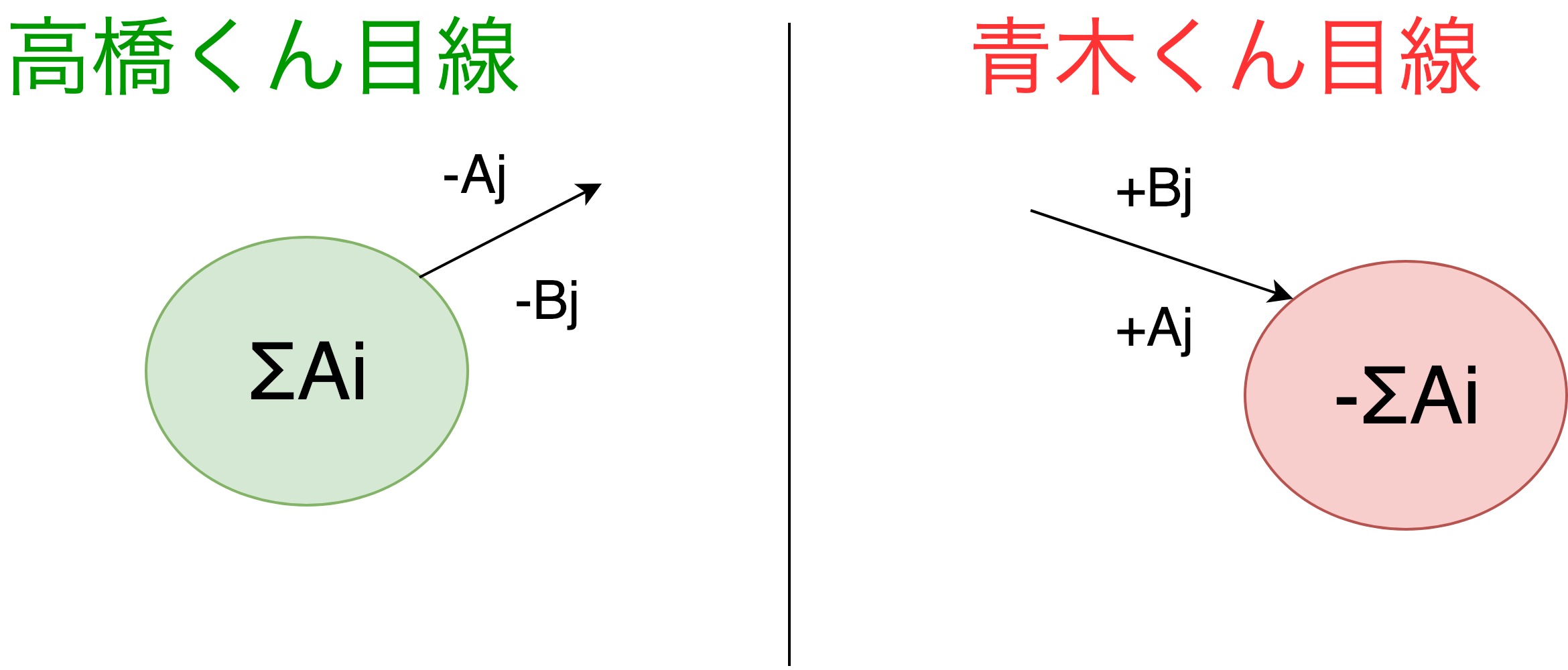
- 相手に皿$j$を取られたとする。すると、高橋くんがもともと持っていた得点から$-Aj$される。さらに、$Bj$が青木くんの得点となる。青木くんの得点は高橋くんにとっては$-Bj$点となる。
- よって、皿$j$を取られると高橋くんは$-(Aj+Bj)$点される。高橋くんはより得点の高くなる皿を死守したいので、$Aj+Bj$が大きい皿を死守するのが最善手となる
青木くんの最善手は?
- 青木くん視点では現在の得点は$-\sum Ai$点である。
- 高橋くんから皿$j$を取ると、自分の得点として$+Bj$される。そして初期状態のうち、$-Aj$がなかったことになるので、青木くんのポイントは$+Aj$される。
- よって、青木くんが皿$j$を取ると、青木くんの得点は$+Aj+Bj$となる。より得点の高い皿を取ったほうがお得なので、青木くんの最善手は$Aj+Bj$が大きいものから取るということになる。
要点
- 2つの要素間で不等式を作る
- 2つの要素を比べて優劣をつけたい時につかう
- $1つ目の要素を何にするか \geq 2つ目の要素を何にするか$みたいな式を立てる
- この考え方を使う問題は結構あるみたい
- この問題ではN=2の実験で使った考え方
- 最初から全部自分のとする考え方
- 自分が取る→相手が取る→自分が取る→…だと状況が複雑
- 最初から全部自分のものとすれば、自分が取られて嫌なものを選ぶだけ
- 相手から見ると、自分が一番撮りたいやつを取るだけ
アルメリアさんいつもありがとうございます
感想
- 愚直に考えるのではなく、自分の考えやすい問題に落とし込むことで解くことができた。
- なんだか騙された気分になる。直感的じゃないので