ABC-C第15弾

• ABC-C第15弾

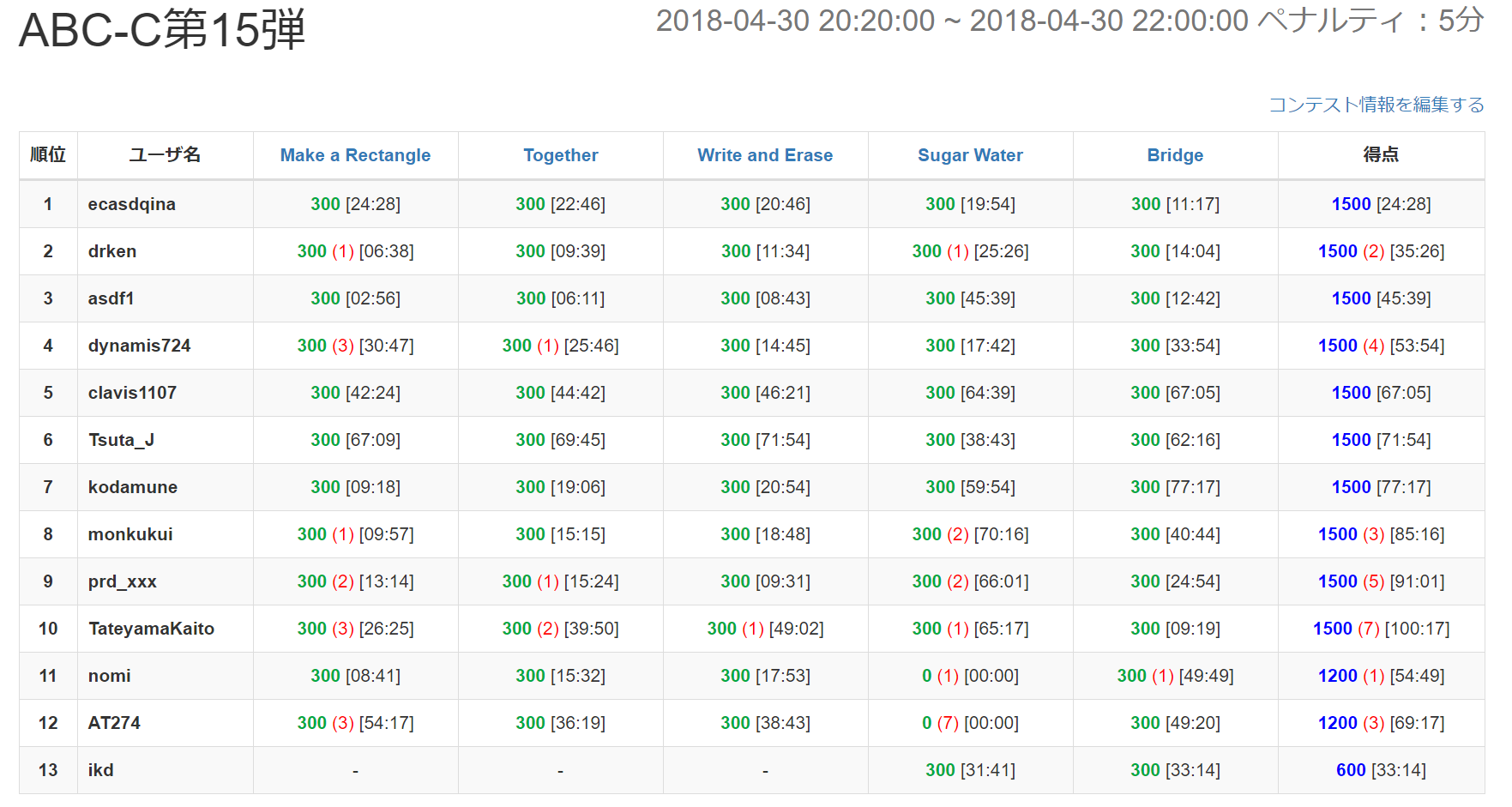
ABC071 「Make a Rectangle」

解法

• 2つの長さが同じやつを見つける。その中から最も長いペアを2つ選ぶ。

コード

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

int main() {
   int N;
   cin >> N;

   map<ll, ll> mp;
   for (int i = 0; i < N; i++) {
      ll a;
      cin >> a;
      mp[a]++;
   }

   vector<ll> v;
   for (auto &x : mp) {
      while (x.second > 0) {
         x.second /= 2;
         if (x.second > 0) v.push_back(x.first);
      }
   }

   sort(v.begin(), v.end(), greater<ll>());

   if (v.size() >= 2) {
      cout << v[0] * v[1] << endl;
   } else {
      cout << 0 << endl;
   }

   return 0;
}

感想

• 2本ペアをどうやって判定するかを考えるのに時間がかかってしまった。

ABC072 「Together」

考察

• 愚直に考えると、ある数を作りたいとき、そのままか、+1か、-1かを試すことになる。だが、それでは$O(N^2)$になってしまい間に合わない。

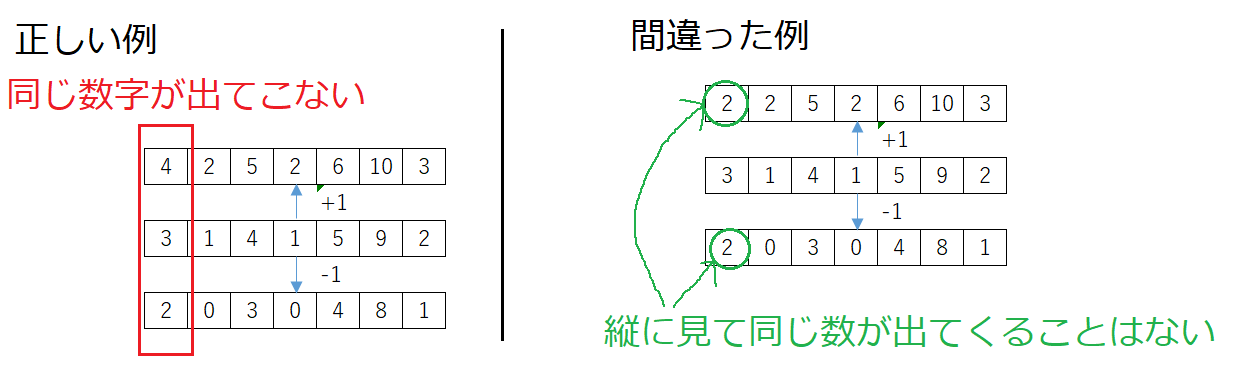
• 元の数列、元の数列+1、元の数列-1をそれぞれ紙に書いてみる。
• すると、縦に見たとき同じ数字が出てこないことに気が付く。

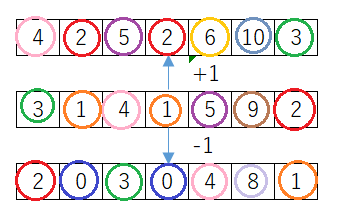
• なので、元の数列、元の数列+1、元の数列-1で出てきた数をカウントすればいいことに気が付く。縦に同じ数字が出てくることはないので、数列を走査するのと同じように数えることができる。

解法

• 元の数列、元の数列+1、元の数列-1を作り、出てきた数字をカウントする。
• カウントが最も多かったものが答えとなる。

コード

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

int main() {
   int n;
   cin >> n;
   map<ll, ll> mp;
   for (int i = 0; i < n; i++) {
      int a;
      cin >> a;
      mp[a]++;
      mp[a-1]++;
      mp[a+1]++;
   }

   ll ans = 0;
   for (auto x : mp) {
      ans = max(ans, x.second);
   }

   cout << ans << endl;

   return 0;
}

感想

• 縦に見た時に数に重複がないってことに気が付くのが大事だったように思う。
• やっぱ紙に書いてみるのは大事だね。

ABC073 「Write and Erase」

解法

• 出てくる数字が奇数回の時その数は残り、偶数回の時その数は消える

コード

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

int main() {
   int n;
   cin >> n;
   map<ll, ll> mp;
   for (int i = 0; i < n; i++) {
      int a;
      cin >> a;
      mp[a]++;
   }

   ll ans = 0;
   for (auto x : mp) {
      if (x.second % 2 == 1) ans++;
   }

   cout << ans << endl;

   return 0;
}

ABC074 「Sugar Water」

バチャコン中の考察

• 4つの操作回数がそれぞれ何回か分れば良い。でも最大で何回操作するか分んない！（ホントはわかるけどこの時点で気づいてなかった）
• なんか問題文から式が作れそうだから作ってみる。
• Aをi回、Bをj回、Cをk回、Dをl回すると考えると以下の2式が作れる
  • $\frac{100(Ck+Dl)}{100Ai+100Bj+Ck+Dl} \leq \frac{E}{100+E}$
  • $100Ai+100Bj+Ck+Dl \leq F$
• 問題文から式を作ることで問題を解くための手がかりをつかめる問題を解いた経験があったため式を作ってみた。でもこの式を20分くらい考えたりいじってみたけど何も発展しない...
• ここで、水と砂糖のそれぞれの組み合わせを独立に作ればいい気がしてきた。この方針で行けそう！って思った。
• ここでバグらせて終了...

理想の考察の流れ

• 問題が複雑なので、何について重点的に考えるかを考えてみる（なんかこれが大事だったりするらしい）。
• 今はいろんな濃度の砂糖水を作ってみたいので、まず水と砂糖を作りたい。できれば組み合わせを全列挙したいので、4つの操作の操作回数の最大値を知りたい。最大値が分かれば全列挙できる。
• 重さの最大値が$F$であることを考慮する。ここで、最大の水、砂糖それぞれの最大の操作回数を求める。水は$A,B=1$のとき$\frac{3000}{100}=30$回が最大の操作回数。砂糖は$C,D=1$のとき$\frac{3000}{1}=3000回$が最大の操作回数となる。
• 水について30回の2重ループを回すと$900$個(?)の水ができる。砂糖について3000回の2重ループを回すと$9 \times 10^{6}$個の砂糖ができる。これを組み合わせるわけだが、普通に組み合わせると$8.1 \times 10^{9}$個の組み合わせができるのでTLEしてしまう。
• そこで、全体の重さが$F$以下になることに注目する。水の組み合わせを生成するとき、重さは最大でも$F$となる。つまり、水の重さは$100 \leq water \leq F$の範囲に収まる。なので、$F$より大きくなる水の組み合わせをはじく。それに加えて組み合わせてできた水の重さをユニークにすれば出来上がる水の個数は$F$個以内に収まる。
• 砂糖の重さについても最大値は$F$のため$1 \leq sugar \leq F$の範囲に収まる。$F$を超えるモノをはじいてからユニークにすると砂糖の組み合わせの個数は$F$個以下になる。
• 水と砂糖は両方とも最大でF個できるので、水と砂糖の組み合わせを2重ループで求めたとしても$O(F^2)$で済む。

解法

• 30回の2重ループを回して水の組み合わせを全列挙する。組み合わせた結果、水の重さが$F$を超えるモノをはじく。組み合わせてできた水の重さはユニークにする。
• 3000回の2重ループを回して砂糖の組み合わせを全列挙する。組み合わせた結果、砂糖の重さが$F$を超えるモノをはじく。組み合わせてできた砂糖の重さはユニークにする。
• 先ほど作った水と砂糖を全通り組み合わせる。その中で条件を満たしつつ濃度が最も高いときの砂糖水と砂糖の重さが答えとなる。

コード

#include <bits/stdc++.h>
using namespace std;

int A, B, C, D, E, F;

int main() {
   cin >> A >> B >> C >> D >> E >> F;

   // 砂糖、水をそれぞれ独立して作る
   set<int> waterSet, sugarSet;

   // 水
   for (int i = 0; i <= 33; i++) {
      for (int j = 0; j <= 33; j++) {
         int w = 100*A*i + 100*B*j;
         if (w <= F) waterSet.insert(w);
      }
   }

   // 砂糖
   for (int i = 0; i < 3010; i++) {
      for (int j = 0; j < 3010; j++) {
         int s = C*i + D*j;
         if (s <= F) sugarSet.insert(s);
      }
   }

   const double nLim = (double)E/(100+E); // 濃度の限界値
   double noudo = -1; // 初期値を-1にしないと一度も更新されなくなってしまう
   int ans1 = 0, ans2 = 0;
   for (int s : sugarSet) {
      for (int w : waterSet) {
         int sum = s + w; // 砂糖水
         if (sum == 0) continue; // 0除算を防ぐため
         double x = (double)s/sum; // 作った砂糖水の濃度
         if (sum <= F && x <= nLim && x > noudo) { // 条件を満たす && 濃度が最大値
            noudo = x;
            ans1 = sum, ans2 = s;
         }
      }
   }
   printf("%d %d\n", ans1, ans2);

   return 0;
}

感想

• いろいろ足りない発想があった
• 何について重点的に考えるかを考えるのが大事らしい(by seicaさん)。今回の場合、出来上がるものに注目する。「いろんな濃度の砂糖水が作りたい→砂糖、水を作る→砂糖と水を全列挙したい→操作回数の範囲を求める」という流れをたどるとよかった。
• 少なくとも1回は更新させたいとき、値は範囲外のものにするっていうやつ、普通に忘れてた。水だけの場合、濃度の初期値を0にすると更新されない。
• コンテスト中、どれだけループを回せばいいかわからなかった。今までの問題は制約にループの回数が素直に書いてあったが、今回はそうではなかった。
• 全列挙をする時は値の範囲を考える。当たり前なんだけど、これを意識したことがなかった。なんか適当にループ回せば全探索できるだろとか思っていつも実装していた。全探索の範囲を考えるとき、制約に素直に書いてあるときもあるが、そうでない時もある。問題の条件や制約から全探索の範囲を考える場合もある。今回は制約に素直に書いてない場合。A, Bの1回の操作は最小で100、重さの最大は3000だから最大の操作回数は30回。C, Dの1回の操作は最小で1、重さの最大は3000だから最大の操作回数は3000回。みたいにしてやる必要があった。
• あるものを作るための材料を分けて考えるという発想がなかった。今回の場合、水と砂糖で砂糖水を作る。だが、それだと複雑なので水は水だけで生成し、砂糖は砂糖だけで生成するという発想がなかった。普通なら4重ループになっていたが、この発想で2重ループにできた。問題が複雑な時は、自分が考えやすいように分割して考えるというのは結構使う気がする。なんか複雑だなーと感じたら要素を分解して考えるといいのかも...
• たくさん生成されるデータを範囲内に絞るという発想がなかった。制約の範囲内に絞れば生成されるデータを限定することができ、計算量が減る。今回の場合、生成される砂糖と水の範囲を1～Fに抑えることで計算量を$O(F^2)$に抑えることができた。

ABC075 「Bridge」

解法

• 制約が小さいので、それぞれの辺を取り除いたときに連結かどうかを調べればいい

コード

#include <bits/stdc++.h>
using namespace std;

int N, M;
int A[100], B[100];
vector<int> G[100];
bool visited[100];

void dfs(int from, int a, int b) {
   visited[from] = true;
   for (int to : G[from]) {
      if (from == a && to == b) continue;
      if (to == a && from == b) continue;
      if (visited[to]) continue;
      dfs(to, a, b);
   }
}

int main() {
   cin >> N >> M;
   for (int i = 0; i < M; i++) {
      cin >> A[i] >> B[i];
      A[i]--, B[i]--;
      G[A[i]].push_back(B[i]);
      G[B[i]].push_back(A[i]);
   }

   int ans = 0;
   for (int i = 0; i < M; i++) {
      fill(visited, visited+N, false);
      dfs(0, A[i], B[i]);
      if (count(visited, visited+N, true) < N) ans++;
   }
   cout << ans << endl;

   return 0;
}

• 僕は隣接リストで実装したけど隣接行列での実装もできるっぽい。隣接行列でDFSとかやったこと無かった...

感想

• 隣接リストで辺を取り除く方法を思いつくのに時間がかかった。
• あと、ループを回すときにNで回してしまった。ホントはMなのに。たまにやらかすのでマジでどうにかしたい