コンテスト中の考察
- なんかめんどくさそうな問題
- 幅の一番狭い道がボトルネックになりそう。理由は、他の道の幅が何であれ結局幅が一番狭い道で人が詰まるから。(その交通機関で何人乗れるかを幅、交通機関の名前はどうでもいいので全部「道」って呼んでます)
- 「一番幅の狭い道を最後の集団が通過するまでの移動回数 + 一番は幅の狭い道を超えてから移動する交通機関の数」で計算できそう
- 青字の部分はどう計算しようか。区間を最初から見ていって、
ans += 残ってる人数 / その区間で通れる人数みたいな感じにすれば良さげ。人数の変数は人数 = 人数 % その区間で通れる人数って更新すれば良さそう - そんな感じで書いて提出したけどWA。
- なんでWAなのかもわからない。あきらめ〜
反省点
WAの原因
- 僕が考えた更新では、一番小さい道路で人が詰まることを考えられてなかった。
- ある道路の幅が3の時は、全体を通して3人ずつ移動するという考察になってしまっていた。実際は一番小さいところで詰まるからこれはだめ。例えば幅3の道路の先に幅2の道路があるとしたら、全体として3人ずつ移動することはできない。
どうすれば良かったか
- ボトルネックの部分を切り離して考えば良かったっぽい?一気に全ての状態を考えてたので複雑すぎて頭爆発してた。
理想の考察
- 色々実験すると、一番幅の狭い通路がボトルネックになりそうだと思う
- 最後の集団がボトルネックの道路を過ぎたら、あとは人が詰まらずにスムーズに進むことがわかる。
- なので、図のような感じのやつを求めればいいことになる。この例では3→4への通路がボトルネックの部分。
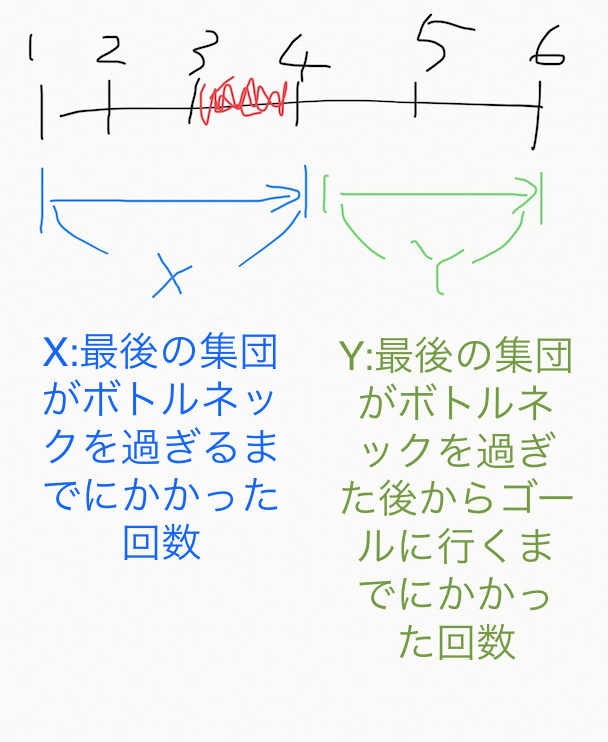
- 全体の構造はわかった。答えはX+Yとなる。そのうち、Yの部分は簡単にわかる。ボトルネックの道路がiだとしたら、Yは5-iとなる。先ほどの例の場合、ボトルネックの道路は3番目なのでYは5-3=2となる。
- 問題なのはXの部分。複雑でよくわからない。Xのうち、この問題をめんどくさくしてるのは明らかにボトルネックの部分。くそが!!なので、ボトルネックの部分だけ取り出して考えてみる
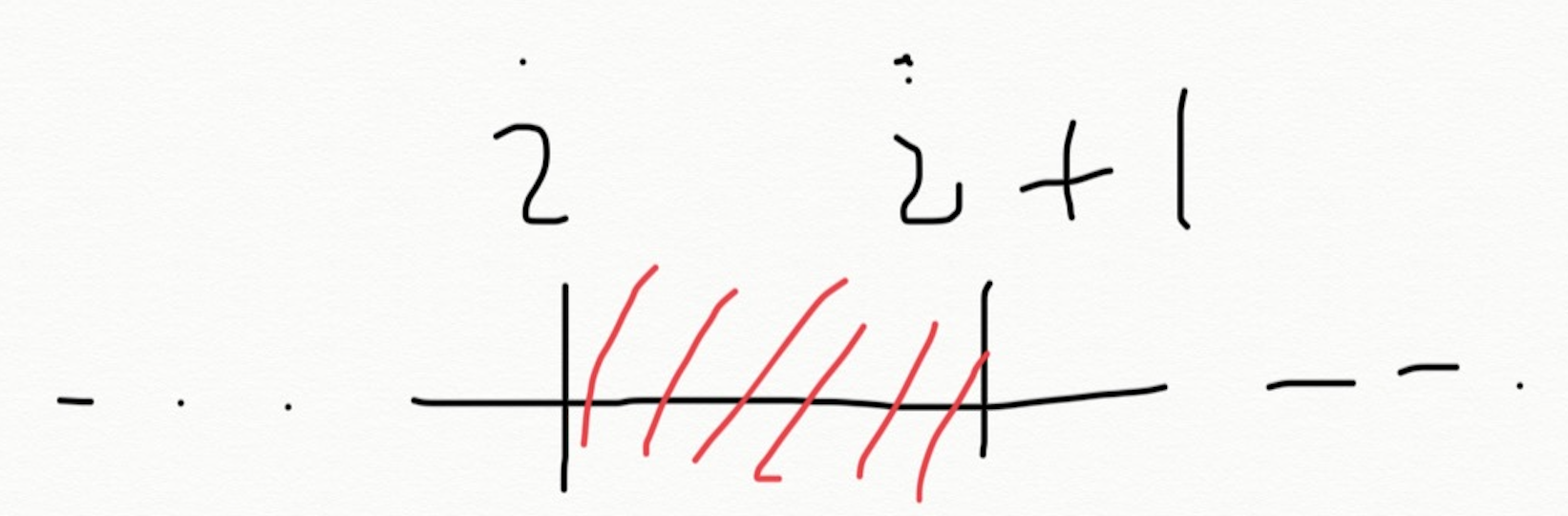
- 以下の図はボトルネックの部分を取り出したやつ。求めたいのは、ボトルネックの部分で人を処理する回数。
- 都市i→i+1への通路の幅をKとする。ここに流れてくる人の数は必ずK人以下となる。理由は、それより前の通路はKより大きいから。これはなんとなく直感的にわかる。ボトルネックの部分では、K人を通らせる→K人を通らせる…という処理を繰り返す。なのでこの部分で人を処理する回数は$\lceil \frac{N}{K} \rceil$回となる。
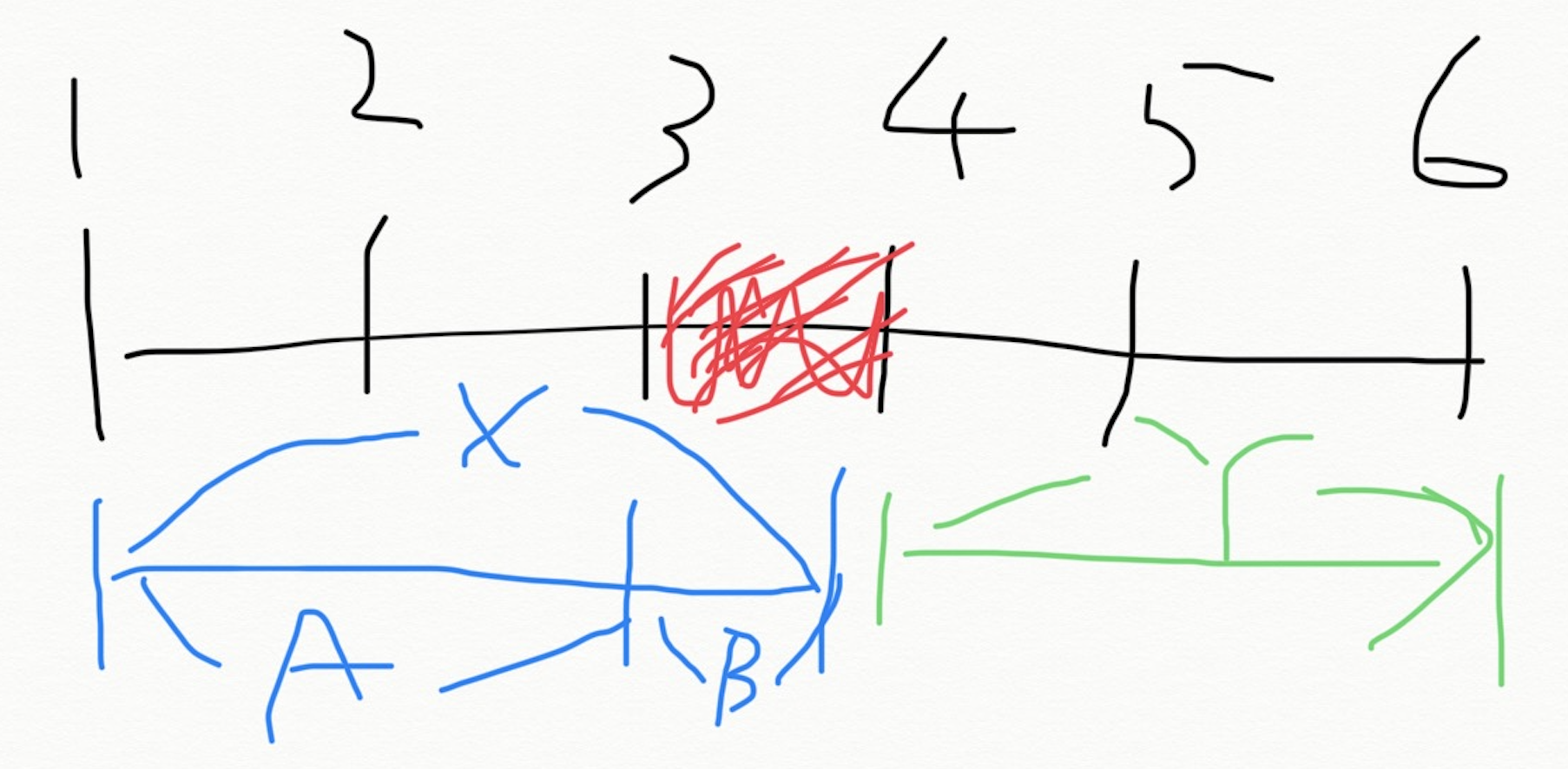
- ちょっと複雑になったので状況を整理する。今の状況は以下のような感じ。さっきまでYがわかってたけどXがわかってなかった。だからXをAとBに分けて考えた。Bはボトルネックの部分で、処理回数は$\lceil \frac{N}{K} \rceil$回とわかった。Bは最初の集団がiに来た時から全員を処理するまでの回数。なのでAは最初の集団がiに行くまでの回数となる。これは簡単で、i回となる。
解法
- 通路の中で一番幅が狭いものがボトルネックとなる。スタートからボトルネックを超えるまでの試行回数をX回、ボトルネックを超えた後からゴールまでの試行回数をY回とする。Yは$5-i$回となるがXはパッと見よくわからない。
- Xは「最初の集団がスタートからボトルネックの通路の前に着くまでの試行回数」と「N人をボトルネック部分で処理するのにかかる回数」の2つに分けることができる。前者は$i-1$回となる。一番狭い幅の通路をKとすると、後者は$\lceil \frac{N}{K} \rceil$となる。
- 答えはX+Yとなる。Xは$i -1+ \lceil \frac{N}{K} \rceil$で、Yは$5-i$。よって$X+Y = A+B+Y =i -1+ \lceil \frac{N}{K} \rceil + 5 - i = \lceil \frac{N}{K} \rceil +4$。答えは$\lceil \frac{N}{K} \rceil +4$となる。
コード
# include <bits/stdc++.h>
using namespace std;
# define int long long
int N;
int A[5];
signed main() {
cin >> N;
int K = 1e18;
for (int i = 0; i < 5; i++) {
cin >> A[i];
if (A[i] < K) {
K = A[i];
}
}
int ans = ((N + K - 1) / K) + 4;
cout << ans << endl;
return 0;
}
要点
- 問題の構造をつかんだら、複雑な部分を分解してく
- コンテスト中の考察でX+Yで答えが出るところまではわかっていた。
- だが、なんか複雑に感じて解けなかった。
- これは複雑にしている部分がボトルネックの部分であることに気づけばXをさらに分解できることに気づくと良かった。
メモ
- けんちょんさんの記事。神。いつもありがとう。
- さらっと記事書いてる感じがするけど理解に1週間くらいかけてる。これを2000人が解いたの信じられないんだが。わけわからん。僕だけ頭のネジ外れてんじゃねーかと思う。
