ABC-C第5弾

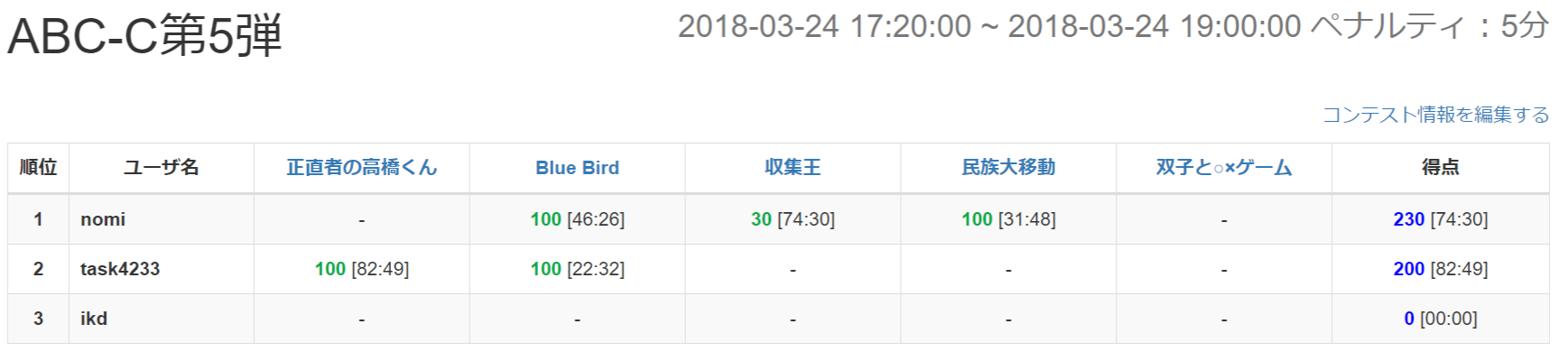
• バチャ
• 2完と部分点1つ。

ABC021 「正直者の高橋くん」

考察

• $a$から$b$への最短距離求めるだけならワーシャルフロイドみたいな最短路アルゴリズムでできそう。
• でも、最短距離になるような経路が何通りあるかがわからん。。。
• とりあえず始点から各頂点への最短距離を求める。
• これは僕のイメージだけど、頂点と辺を結ぶ構造の最短路を求めると言われたらダイクストラ法が一番最初に思い浮かぶ。というわけで、最短距離はダイクストラ法で求める。
• 最短距離は求められたけど、経路数をどうやって求めようか？
• ここで、最短経路をたどったときの図を書いてみる。

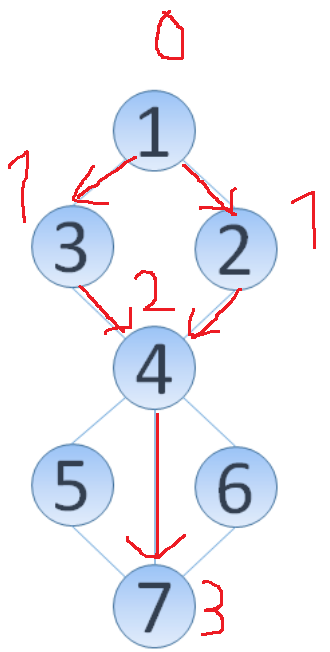
• 赤い線は、最短路に関係のある部分だけ書いた。書いてある数字は距離を表す。最短経路の数は、この赤い線に沿って数えれば求められそう。

• この赤い線は、ダイクストラ法で頂点を遷移するときに通る。なので、ダイクストラ法で最短経路を求めるついでに経路の数え上げもできそうだと気づく。

• 最短経路の赤い線に沿って経路数を数える図を書いてみる

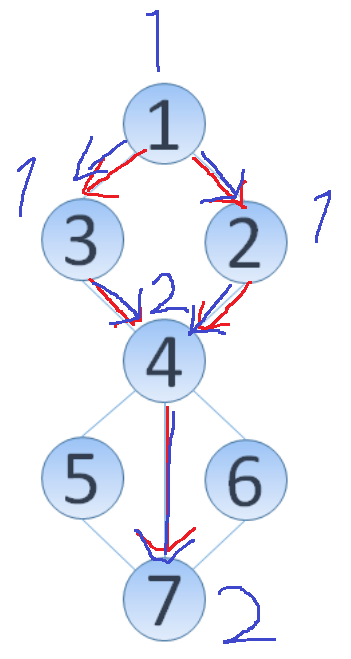
• 青い線は最短経路をなぞった経路数数え上げの線で、数字はその頂点までの経路数を表す。
• どうやら経路数は、以下のように求められそう
  • 始点の経路数を1とする。
  • 始点からダイクストラ法の流れに沿って経路数を求めていく。
  • 遷移先の頂点が最短経路となるならば、今見ている頂点までの経路数を遷移先の頂点に足し合わせる。
• こんな感じで考察終了！

解法

• 最短経路のDAGを作る
• 作ったDAGに沿って最短経路の個数を数え上げていく。

実装

• 自分が解くとしたら一番最初にダイクストラ法が思い浮かぶので、ダイクストラ法でコードを書いた。
• ただ、遷移のコストが1なので、典型的なBFSでも解くことができる。

BFSでの実装

• BFSでの実装

ダイクストラ法での実装

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

// {この頂点への最短距離, この頂点の番号} を管理する構造体
struct P {
   int dist, num;
   // デフォルト(大きい値が先頭)
   bool operator<(const P &p) const {
      return dist < p.dist;
   }
   // greater(小さい値が先頭)
   bool operator>(const P &p) const {
      return dist > p.dist;
   }
};

vector<vector<int>> G;
const int mod = 1e9+7;
const int INF = 1e8;
int N, a, b, M;
int dist[111]; // dist[i]: aからiまでの最短距離
ll cnt[111]; // cnt[i]: aからiまで最短距離で来る個数

void dijkstra(int s) {
   // 初期化
   fill(dist, dist + N, INF);
   dist[s] = 0;
   priority_queue<P, vector<P>, greater<P>> Q;
   Q.push({0, s});
   cnt[s] = 1; // いつもと違って、経路数を求める配列があるのでそれも初期化する

   while (Q.size()) {
      P p = Q.top(); Q.pop();
      int v = p.num; // 今見ている頂点
      if (dist[v] < p.dist) continue;
      for (int t : G[v]) {
         if (dist[t] > dist[v] + 1) {
            dist[t] = dist[v] + 1;
            Q.push({dist[t], t});
         }
         // 今見ている頂点が最短経路上にあるならば、前の頂点からのカウントを足し合わせる
         if (dist[t] == dist[v] + 1) {
            cnt[t] += cnt[v];
         }
      }
   }
}

int main() {
   // 入力
   cin >> N >> a >> b >> M;
   a--, b--;
   G = vector<vector<int>>(N);
   for (int i = 0; i < M; i++) {
      int x, y;
      cin >> x >> y;
      x--, y--;
      G[x].push_back(y);
      G[y].push_back(x);
   }

   // ダイクストラ法
   dijkstra(a);

   // 出力
   cout << cnt[b] % mod << endl;

   return 0;
}

感想

• この問題、数ヶ月前に解説読んでもよくわからなかったので理解できて良かった（のしさんありがとう...
• 数ヶ月前にできなかったのは、「DAGという馴染みのない言葉＋DPで解く＋最短路アルゴリズムを知らない」という理由でびびったから。
• 最短路上を数え上げDPすれば最短路を通る経路の個数を求めることができるというのは典型らしいので覚えておきたい。
• この問題で大事だったのは、最短経路の遷移だけに注目することだったように思う。

ABC022 「Blue Bird」

考察

• あー、なんか最短路アルゴリズム使えそうってなるけど、何も考えずに使ったら解けなさそう
• でも、最短路アルゴリズム使った方が絶対楽に解ける。
• 始点を取り除けば何も気にせずに最短路アルゴリズムが使えそう。
• あとは、1から始まってどこを通過して1に戻ってくるかというのをすべて試せばいい
• 考察終了！

解法

1. 始点を除く頂点でワーシャルフロイド法をする。
2. dist[0][i] + dist[i][j] + dist[j][0] を最小化する。i, jはループで回す

コード

#include <bits/stdc++.h>
using namespace std;

const int INF = 1e8;
int B[333][333];

int main() {
   // 初期化
   fill(B[0], B[333], INF);

   // 入力
   int N, M;
   cin >> N >> M;
   for (int i = 0; i < M; i++) {
      int a, b, c;
      cin >> a >> b >> c;
      a--, b--;
      B[a][b] = B[b][a] = c;
   }


   // ワーシャルフロイド法
   for (int k = 0; k < N; k++) {
      for (int i = 0; i < N; i++) {
         for (int j = 0; j < N; j++) {
            if (i == 0 || j == 0 || k == 0) continue;
            B[i][j] = min(B[i][j], B[i][k] + B[k][j]);
         }
      }
   }

   // 1 -> どこか -> 1 の最短距離を探す
   int ans = INF;
   for (int i = 0; i < N; i++) {
      for (int j = 0; j < N; j++) {
         if (i == j) continue;
         int t = B[0][i] + B[i][j] + B[j][0];
         ans = min(ans, t);
      }
   }

   cout << (ans==INF ? -1 : ans) << endl;

   return 0;
}

感想

• 以前解いたときの記憶が残っていたのですんなり解けた。
• こんな感じで解いた問題全部覚えれたらいいのになー。

ABC023 「収集王」

部分点取るぜ！

• こんな感じ！
• 部分点がとれるだけの座標の配列を用意して、愚直に求めていく。
• まあ、正直この部分点解法を発展させたところで満点解法は導けないのでチャチャっと流す

満点解法

考察

• 愚直にやるのは自明にダメ。じゃあどうすれば？？？
• アメがＫ個となるような行と列の組み合わせを考える。その例として、アメが0個となるような行の数、アメがＫ個となるような列の数を求めてやる必要がある。もっと一般的に言うと、アメが$i$個となるような行の数、列の数を求める。そうすれば、あとはそれらを上手い子と組み合わせて考える。

解法

1. アメが$i$個となるような行が何行あるか、アメが$i$個となるような列が何列あるのかを求める。
2. 先ほど用意した配列を使って、アメがＫ個になる組み合わせを求める
3. アメのある座標を見て、その行にあるアメ個数と列にあるアメの個数の和がＫになっていたらカウントをデクリメントする。

• この操作をする理由は、赤丸の座標を見た時、2の操作ではアメの個数を4個と数えてしまうためである。
• つまり3の操作は、操作2でＫ個と数えてしまった分のカウントを引いているということ。

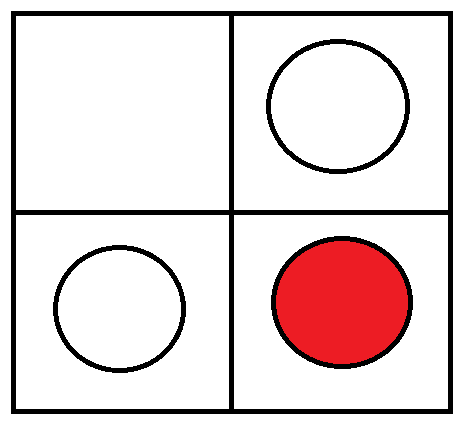
1. アメのある座標を見て、その列にあるアメの個数と行にあるアメの個数の和がK+1になっていたらカウントをインクリメントする。

• この操作では、操作2で数てない分を補っている。

コード

#include <bits/stdc++.h>
using namespace std;

const int M = 111111;
int R, C, K, N;

// アメがある座標の情報
int r[M], c[M];

int a[M]; // a[i]: i行目のアメの個数
int b[M]; // b[i]: i列目のアメの個数

int x[M]; // x[i]: アメがi個ある行の個数
int y[M]; // y[i]: アメがi個ある列の個数

int main() {
   cin >> R >> C >> K >> N;
   for (int i = 0; i < N; i++) {
      cin >> r[i] >> c[i];
      r[i]--, c[i]--;
      a[r[i]]++, b[c[i]]++; // i行目、i列目のアメの個数をインクリメント
   }

   // アメがa[i]個ある行の個数をインクリメント
   for (int i = 0; i < R; i++) x[a[i]]++;
   // アメがb[i]個ある列の個数をインクリメント
   for (int i = 0; i < C; i++) y[b[i]]++;

   long long ans = 0;

   // 行と列のアメの個数の和がKになる組み合わせの個数を足していく
   for (int i = 0; i <= K; i++) {
      int j = K - i;
      ans += x[i] * y[j];
   }

   // アメのある座標を見て、行、列のアメの和がK個になっていたらカウントをデクリメント
   for (int i = 0; i < N; i++) {
      if (a[r[i]] + b[c[i]] == K) ans--;
   }

   // アメのある座標を見て、行、列のアメの和がK+1個になっていたらカウントをインクリメント
   for (int i = 0; i < N; i++) {
      if (a[r[i]] + b[c[i]] == K+1) ans++;
   }

   cout << ans << endl;

   return 0;
}

感想

• いやいや、むずい。
• 考察むずいしコードバグりやすいし。
• この問題で大事だったのは、アメがＫ個になるようなパターンのみに注目することだったように思う。
• どうすれば解法思いつくんだよって感じの問題。解説ACでも頭爆発したのに

ABC024 「民族大移動」

解法

• 貪欲法で解く
• それぞれの日において、移動できるときはできるだけ目的地に近づくように移動する。

コード

• コンテスト中に書いたコード
  • このコードは汚いので上位陣のコードを見て書き直す(いつか

コード

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

ll N, D, K;
ll L[11111], R[11111];
ll S[11111], T[11111];
char houkou[11111]; // houkou[i]: 民族iが右方向に進むなら'R',左方向に進むなら'L'
ll day[11111]; // day[i]: 民族iが目的地にたどり着くまでの日数

int main() {
   cin >> N >> D >> K;
   for (int i = 0; i < D; i++) cin >> L[i] >> R[i];
   for (int i = 0; i < K; i++) {
      cin >> S[i] >> T[i]; 
      // 民族の進む方向を定める
      if (S[i] < T[i]) houkou[i] = 'R';
      if (S[i] > T[i]) houkou[i] = 'L';
      day[i] = -1;
   }

   for (int i = 0; i < D; i++) { // i日目の移動
      ll l = L[i], r = R[i];
      for (int j = 0; j < K ; j++) { // 民族jについて
         if (S[j] >= l && S[j] <= r) { // 民族に居場所が移動範囲内にある
            if (houkou[j] == 'R') { // 右に行くタイプの民族
               S[j] = max(S[j], r); // S[j]をできるだけ右に近づける
               if (day[j] == -1 && S[j] >= T[j]) day[j] = i+1;
            } else { // 左に行くタイプの民族
               S[j] = min(S[j], l); // S[j]をできるだけ左に近づける
               if (day[j] == -1 && S[j] <= T[j]) day[j] = i+1;
            }
         }
      }
   }

   // 最後にまとめて出力する
   for (int i = 0; i < K; i++) {
      cout << day[i] << endl;
   }

   return 0;
}

• もっときれいに実装できるかもしれないけど、今の自分にはこれが精いっぱい。。。

感想

• この問題も以前解いたときの記憶が残ってたのですんなり解けた。

ABC025 「双子と○×ゲーム」

問題概要

• なにも書いていない$3\times 3$ の盤面がある。
• 直大くんがo、直子さんがxを盤面に交互に書いていく。このとき両者は、自分の得点ができるだけ多くなるように最善手を打つ。
• 盤面が全て埋まったとき、直大くんと直子さんのスコアをそれぞれ求める。

考察

• どの位置に文字を書いていくのが最善手になるのかを考える。
• 直大くんが塗った隣のマスに直子さんが塗れば、隣り合う文字が異なることになる。隣り合う文字が異なった場合直子さんの得点になるため、直子さんにとっての最善手は直大君の邪魔をすること？直大君のマスに隣り合うマスの内、得点が大きいものを塗るのがよさそう
• なんかあってそうだけど、それがホントに最善手？
• みたいな感じでいろいろ考察する。
• 自分の手番で自分の得点が最大になるような手を打ち、相手の手番で自分の得点が最小になるようにすればいいんだろうなーと思う。でも、1手目をどこに打つか考えるとき、自分の得点が最大になるような場所なんてわかるわけがない。
• なので、最終手番から考える。まず、2人の局面をゲーム木として再帰的に全列挙する。そして、最終手番を見て直大くんの得点が最大のものを選ぶ。次に最終手番の1つ前の手番を見て、直大君の得点が最小になるものを選ぶ。直大君の得点が最小になるように選ぶと、直子さんにおって　その手は最善手となる。
• こんな感じで解けばいいのでは？って感じで考察終了

解法

ミニマックス法

• 自分にとって最も有利な手を打ち(max)、次に相手が自分にとって最も不利な手を打つ(min)。これを繰り返すことで毎回互いに最善手を打つ。
• このアルゴリズムをミニマックス法と呼ぶ。
• ミニマックス法で評価に使う得点を求めるには、ゲーム木探索をする。

ゲーム木探索

• ゲーム木探索では、盤面の状態を探索していく。
• 今回の場合、盤面が少ないので全盤面を探索することができる。
• 以下のゲーム木の画像では最小限の盤面しか載せてないが、ホントはもっと莫大な量の盤面が作られる。
• 今回の場合、1手目が9通り、2手目が8通り、3手目が7通り、... と続いていく。よって盤面は$9!$通りとなる。

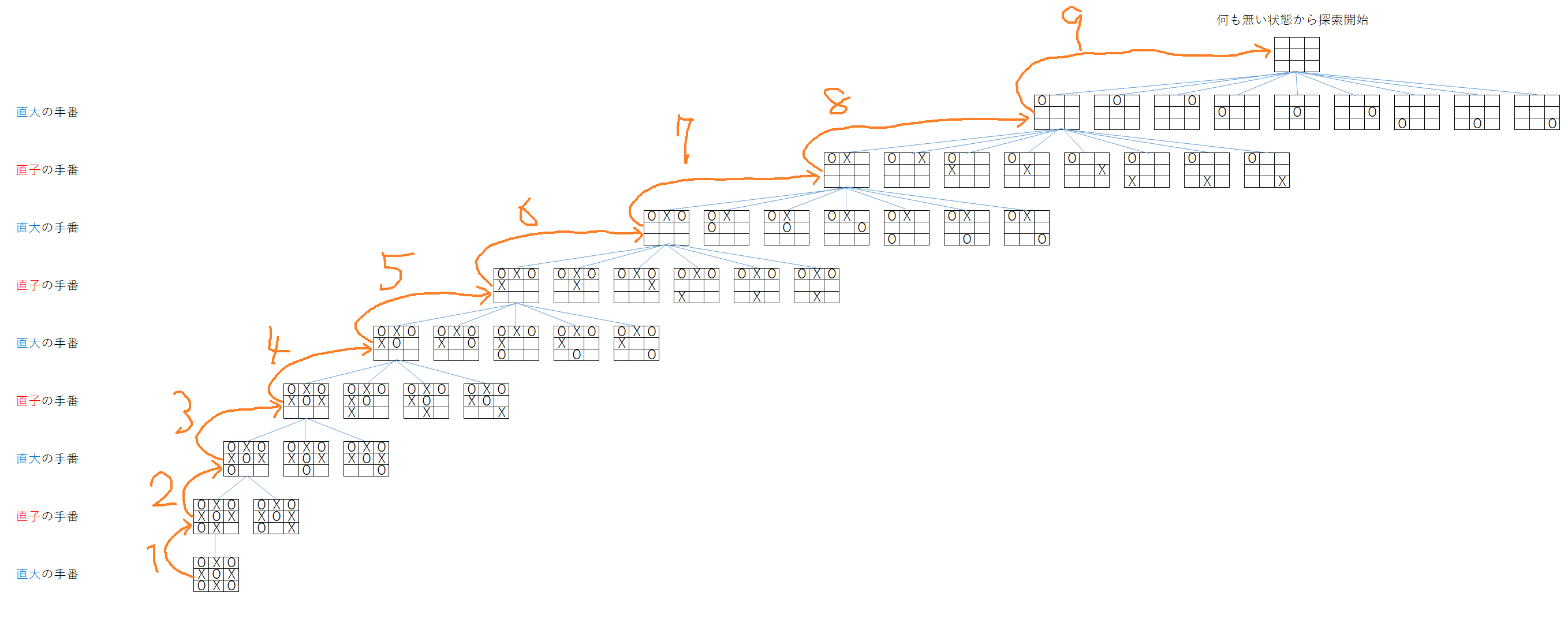
1. 盤面が全て埋まったので、その時のスコアを返す(直大の操作)
2. 盤面を8つ埋めた状態の内、スコアが最小になるものを返す(直子の操作)
3. 盤面を7つ埋めた状態の内、スコアが最大になるものを返す(直大の操作)
4. 盤面を6つ埋めた状態の内、スコアが最小になるものを返す(直子の操作)
5. 盤面を5つ埋めた状態の内、スコアが最大になるものを返す(直大の操作)
6. 盤面を4つ埋めた状態の内、スコアが最小になるものを返す(直子の操作)
7. 盤面を3つ埋めた状態の内、スコアが最大になるものを返す(直大の操作)
8. 盤面を2つ埋めた状態の内、スコアが最小になるものを返す(直子の操作)
9. 盤面を1つ埋めた状態の内、スコアが最大になるものを返す(直大の操作)
   • この9番目の操作で全ての盤面が収束する。
   • その中でスコアが最大のものを選ぶことで操作が終了する。

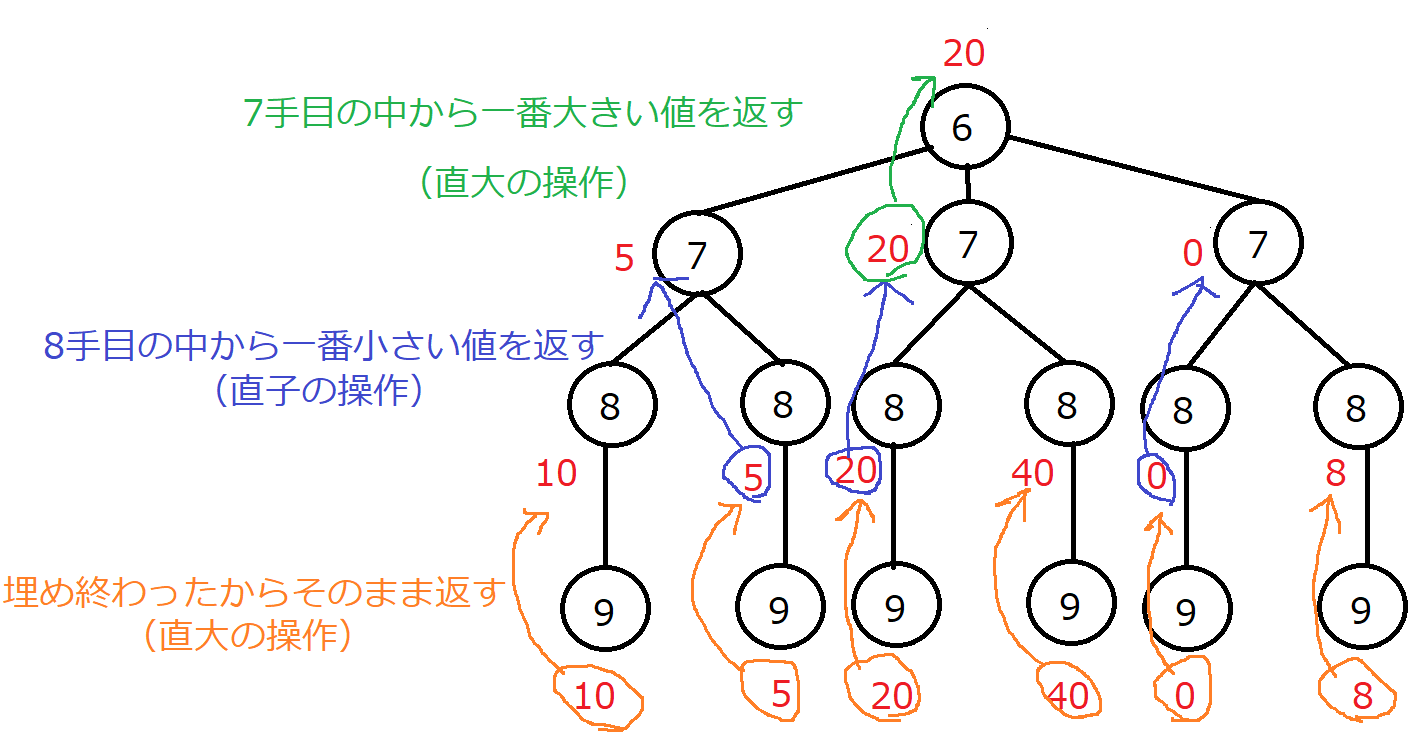
ゲーム木の一部分を見てみる

• 全体を眺めていても、どんな処理が行われるかイメージが付きにくい。
• なので、ゲーム木の末端を見てみる。
• 以下の図の場合、最終的にこの末端の6手目の値は20となる。

解法まとめ

• ミニマックス法で解く。

コード

#include <bits/stdc++.h>
using namespace std;

char A[5][5]; // 盤面の情報
int b[5][5], c[5][5]; // 得点の情報

// 盤面を埋め終わったとき、直大の得点を返す
int calc() {
   int score = 0;
   // b[2][3]についての直大の得点
   for (int i = 0; i < 2; i++) {
      for (int j = 0; j < 3; j++) {
         if (A[i][j] == A[i+1][j]) score += b[i][j];
      }
   }
   // c[3][2]についての直大の得点
   for (int i = 0; i < 3; i++) {
      for (int j = 0; j < 2; j++) {
         if (A[i][j] == A[i][j+1]) score += c[i][j];
      }
   }
   return score;
}

// 盤面を全通りに埋めるDFS
int dfs(int turn) {
   if (turn == 9) return calc();

   if (turn % 2 == 0) { // 直大の手番
      int Max = -1;
      for (int i = 0; i < 3; i++) {
         for (int j = 0; j < 3; j++) {
            if (A[i][j] != '*') continue;
            A[i][j] = 'o'; // 盤面に'o'を打つ
            Max = max(Max, dfs(turn + 1));
            A[i][j] = '*'; // 盤面を元に戻す
         }
      }
      return Max;
   } else { // 直子の手番
      int Min = 1e8;
      for (int i = 0; i < 3; i++) {
         for (int j = 0; j < 3; j++) {
            if (A[i][j] != '*') continue;
            A[i][j] = 'x'; // 盤面に'x'を打つ
            Min = min(Min, dfs(turn + 1));
            A[i][j] = '*'; // 盤面を元に戻す
         }
      }
      return Min;
   }
}

int main() {
   // 入力
   int sum = 0; // 全体の合計
   for (int i = 0; i < 2; i++) {
      for (int j = 0; j < 3; j++) {
         cin >> b[i][j];
         sum += b[i][j];
      }
   }
   for (int i = 0; i < 3; i++) {
      for (int j = 0; j < 2; j++) {
         cin >> c[i][j];
         sum += c[i][j];
      }
   }

   // 盤面を全て'*'で初期化
   fill(A[0], A[5], '*');

   int chokudai = dfs(0); // 直大の得点が返ってくる
   cout << chokudai << endl;
   cout << sum - chokudai << endl; // 直子の得点は(合計 - 直大の得点)となる

   return 0;
}

ミニマックス法のコード

• ミニマックス法のコードの書き方わかんねーって思ってググったらWikiにミニマックス法のテンプレートが載ってた。
• 疑似コードが載ってるけどなんかごちゃごちゃして見にくいので自分なりにC++で書いてみる

char Board[H][W]; // ゲームの状態を持つ

// 盤面を評価する関数。自分の得点を求める。
int value() {
    // 中身を書く
}

int MIN_MAX(int turn) {
    // 終局したら盤面の値を返す
    if (turn == END) return value();
    
    if (/*自分の局面*/) {
        int Max = -INF;
        for () {
            // 今の盤面で自分が打てるすべての状態を列挙
            Max = max(Max, MIN_MAX(turn + 1));
        }
        return Max;
    } else { // 相手の局面
        int Min = INF;
        for () {
            // 今の盤面で相手が打てるすべての状態を列挙
            Min = min(Min, MIN_MAX(turn + 1));
        }
        return Min;
    }
}

int main() {
    // こんな感じで呼び出せば自分の得点の最大値を知ることができる。
    int myPoint = MIN_MAX(0);
}

おまけ

• ゲーム系の問題は、以下の3つのどれかで解けるらしい

1. 後ろから探索する
2. Grundy数を求める
3. ad hocな必勝法を見つける

• ソースはこれ

感想

• ムズ過ぎない？
• なーにがミニマックス法じゃい。そんなん知らんわってなった。
• 偉そうに解説とか書いたけど、僕もよくわかってない。
• ミニマックス法で解けるらしいけど、この方法はいつ使えるのかもよくわからない。ゼロ和ゲームでなら使えるとか書いてある記事あるけど、ゼロ和ゲームであるかどうかの判断方法が分からない。将棋もゼロ和ゲームらしいけどは？？？って感じ。どこら辺がゼロ和なの？？？
• 某氏にこの記事をおすすめされたけどよくわからん。
• 深入りすると、この問題だけに固執してINF日経ちそうなのでこの程度の理解でいったん切り上げる。
• とりあえず、両者が自分の利益を最大化するとき、プレイヤーＡ目線で見ると以下のようになる。
• プレイヤーＡの利益を最大化する。プレイヤーＡの利益を最小化する。この操作を繰り返すことで両者が常に最善手を打つ。
• この方法が使えそうなときは、ミニマックス法を使うって感じ？
• ゲーム問題は、後ろから探索するかGrundy数を求めるかad hocな必勝法を見つけることで大体解けるみたいなので、その辺を意識していきたい。