- ABC-Cバチャ第10弾
- 苦手な問題が多かった気がする(実装がちょっと複雑なやつ)
- 後ろの3問の実装がちょっと手こずった
ABC046 「AtCoDeerくんと選挙速報 / AtCoDeer and Election Report」
考察の流れ
- $a_i, b_i$が与えられたとき、2人の投票数はそれぞれ$a_ix_i, b_ix_i$となる。
- $x_i$をなるべく小さくなるような条件を満たす最小の$x_i$を求めたい。
- 条件は、両者において今の得票数が前の得票数以上であること。この式を作ればいい感じに答えが求められそう
考察と解法
- 入力と実際の値を表にすると以下のようになる。
- $a,b$は入力で、$x$は、問題文の条件を満たすような最小の値とする。
| 入力 | 実際の値 |
|---|---|
| $a_1:b_1$ | $a_1 x_1, b_1 x_1 $ |
| $a_2:b_2$ | $a_2 x_2, b_2 x_2 $ |
| $a_3:b_3$ | $a_3 x_3, b_3 x_3 $ |
| ... | ... |
| $a_N:b_N$ | $a_N x_N, b_N x_N $ |
- この表の「実際の値」に注目すると、以下の式を作ることができる。
\left\{
\begin{array}{ll}
x_i = 1 & (i = 1) \\
a_ix_i \geq a_{i-1}x_{i-1} & (i \geq 2) \\
b_ix_i \geq b_{i-1}x_{i-1} & (i \geq 2)
\end{array}
\right.
- 今知りたい値は$x_i$なので、先ほどの式を以下のように変形する。
\left\{
\begin{array}{ll}
x_i = 1 & (i = 1)\\
x_i \geq \frac{a_{i-1}x_{i-1}}{a_i} & (i \geq 2) \\
x_i \geq \frac{b_{i-1}x_{i-1}}{b_i} & (i \geq 2)
\end{array}
\right.
- 目的は$x_i$を最小化することである。なので、右辺の値を切り上げた値が最適になることが分かる。例を示して考えると、上記の式から$x_i \geq 2.4$が導き出されたとき、$2.4$を切り捨ててしまっては$x_i = 2$となってしまい条件を満たさないからである。値を切り上げれば条件を満たす最小の整数を求めることができる。先ほどの例で示すと、$x_i \geq 2.4$を切り上げて$x_i=3$となる。
- よって、以下のように式変形する。
\left\{
\begin{array}{ll}
x_i = 1 & (i = 1) \\
x_i = \lceil \frac{a_{i-1}x_{i-1}}{a_i} \rceil & (i \geq 2) \\
x_i = \lceil \frac{b_{i-1}x_{i-1}}{b_i} \rceil & (i \geq 2)
\end{array}
\right.
- $x_i$についての式が2つあるわけだが、どちらを選ぶべきなのか?それは、2つの内の大きい方の値である。なぜなら、$x_i$を小さい方の値に合わせてしまうと、$a_ix_i, b_ix_i$としたときに片方の値が前の値より小さくなってしまい条件を満たさなくなってしまうからである。
- 最終的に、$x_i$は以下の式で求めることができる
\left\{
\begin{array}{ll}
x_i = 1 & (i = 1) \\
x_i = max(\lceil \frac{a_{i-1}x_{i-1}}{a_i} \rceil, \lceil \frac{b_{i-1} x_{i-1}}{b_i} \rceil) & (i \geq 2)
\end{array}
\right.
- $x_i$の求め方が分ったため、後は入力された値と掛け合わせていけば最適な値になる。
備考
- $\lceil a\ \rceil$は$a$の切り上げっていう意味の数学記号。
- 天井関数っていう名前があるらしい。ソースはここ
コード
# include <bits/stdc++.h>
using namespace std;
using ll = long long;
ll N;
ll a[1111], b[1111];
int main() {
cin >> N;
for (int i = 0; i < N; i++) cin >> a[i] >> b[i];
ll n = 1;
ll x = 1, y = 1;
for (int i = 0; i < N; i++) {
if (i == 0) {
n = 1;
} else {
n = max((a[i-1]*n + a[i]-1) / a[i], (b[i-1]*n + b[i]-1) / b[i]);
}
x = a[i] * n;
y = b[i] * n;
}
cout << x + y << endl;
return 0;
}
感想
- 問題文から式を作るという発想がすっっっごく大事だったと思う。いつもこれができない...
- 式に関する発想は以下の3つ
- 比の形が与えられた→$a_ix_i, b_ix_i$の形になる
- 前の投票数が今の投票数以上になるという不等式を作る。
- 不等式をいい感じに変形する
- 入力に対して実際の値がどうなるかを図で書けば思いつけるのか?まずあの表が自分で思いついて書けない気がするんだが。
- あと、式を作ってからその式を変形して使うというね。これも苦手なんだよな-。言われてみればそうだなって感じだけど自分で思いつけない。
- あと、自分が比率を全然分ってなかった(これはマジでひどい)。$a:b$という比率があったときに、両方に違う数を掛けたら比率が崩れると思ってなかった。例えば、$2:3$という比率の左に$5$、右に$6$を掛けたら比率が$5:9$に変わってしまう。でも、**同じ数を掛ければ比率は崩れない!!**これ多分小学生レベルの知識なんだよなー。
- 自分で思いついてこの問題を解けない気がするのでなんかもやもやが残る。
ABC047 「一次元リバーシ / 1D Reversi」
考察と解法

-
xとoの境目に赤い境界線を引いて考える。 - 一度の操作でできることは、この境界線を1つ取り除くことである。
- 一度に1つより多い数の境界線を取り除くことができるかを考える。無理だとわかる。
- よって、一度の操作で1本の境界線を取り除く操作を繰り返すことが最善となる。なので、答えは境界線の本数となる。
コード
# include <bits/stdc++.h>
using namespace std;
int main() {
string s;
cin >> s;
int cnt = 0;
int n = s.size();
for (int i = 1; i< n; i++) {
if (s[i-1] != s[i]) cnt++;
}
cout << cnt << endl;
return 0;
}
感想
- この操作が最善であるいい感じの証明ができないのでちょっとモヤモヤする。いや、証明はたぶんできてるけど自分が納得できてない。
ABC048 「Boxes and Candies」
考察と解法
-
配列の最初の要素の次の要素から走査していく。
-
そのとき、奥の値を優先して操作する。なぜなら、奥の値は次の操作でも使うからだ。
-
配列の2つの要素を見た時のパターンを考える。
-
見ている配列の2つの要素を$a, b(a<b)$とする。
-
2つの要素の合計値を$sum=a+b$とする。
- $sum \leq x$のとき、操作する必要はない。
- $sum > x$のとき、差分$diff = sum - x$とする。答えに差分である$diff$を加算する。
- $diff > b$のとき、$b$に0を代入する
- $diff\leq b$のとき、$b$から$diff$を引く
実装
- 実装でかなり手こずってしまい、コンテスト中はこんなクソコードを生成してしまった。
- 実装を楽にするには、必要な部分のみを考えるという発想が必要だった。
- 気づくべきだったのは、$sum>x$のときに答えに加える数値は$sum - x$に確定しているという点。僕はなぜかここを場合分けによって違う処理をしてしまう。
- 差分を取るのが最善策なので当たり前なんだが気づかなかった...これに気づいていれば実装をバグらせずに済んだんだろうなーと思う。
コード
# include <bits/stdc++.h>
using namespace std;
using ll = long long;
ll N, x;
ll a[111111];
int main() {
cin >> N >> x;
for (int i = 0; i < N; i++) cin >> a[i];
ll ans = 0;
for (int i = 1; i < N; i++) {
ll sum = a[i-1] + a[i];
if (sum > x) {
ll diff = sum - x;
ans += diff;
if (diff > a[i]) {
a[i] = 0;
} else {
a[i] -= diff;
}
}
}
cout << ans << endl;
return 0;
}
感想
- 答えに加える数は毎回$sum-x$という点に気が付いていればよかった。
- 処理が共通な部分で場合分けをして、違うコードで同じ処理を行うやつをやらかした
- 実装を楽にするには、処理が共通した部分を考えることと、必要な部分のみを考えるということが大事だなーと思った。
ABC049 「白昼夢 / Daydream」
解法
自分の解法
-
dreameraserとdreameraserが注意すべき文字列なので最初に判定する。 - そのあと、文字数が多い順に判定する。そうでないと
dreamerの場合、dreamerかもしれないのにdreamとして判定されてしまうかもしれない - 自分の解法コード
- この解法ではコードが複雑になってしまってよくない。
想定解法
- 4つの文字列について、逆から読めば文字列が一意に定まる。
dreamとdreamerのどちらかわからないという状況は発生しなくなる。
想定解法コード
# include <bits/stdc++.h>
using namespace std;
vector<string> S = {"dreamer", "dream", "erase", "eraser"};
int main() {
string s;
cin >> s;
reverse(s.begin(), s.end());
for (int i = 0; i < S.size(); i++) {
reverse(S[i].begin(), S[i].end());
}
int n = s.size();
for (int i = 0; i < n; ) {
bool ok = false;
for (int j = 0; j < S.size(); j++) {
if (s.substr(i, S[j].size()) == S[j]) {
i += S[j].size();
ok = true;
break;
}
}
if (!ok) {
puts("NO");
return 0;
}
}
puts("YES");
return 0;
}
DP解法
- 上位陣のコードにDPが多かったため、僕もDPで解いてみた
DP解法
# include <bits/stdc++.h>
using namespace std;
vector<string> S = {"dreamer", "dream", "erase", "eraser"};
bool dp[111111];
int main() {
string s;
cin >> s;
dp[0] = true;
for (int i = 0; i <= s.size(); i++) {
for (int j = 0; j < S.size(); j++) {
int size = S[j].size();
if (i >= size) {
dp[i] |= dp[i-size] && s.substr(i-size, size) == S[j];
}
}
}
puts(dp[s.size()]?"YES":"NO");
return 0;
}
感想
- 簡単に実装するための工夫って大事だなーって思った。
- 自分の解法の場合、FizzBuzzみたいにif文を書く順番を気にする必要があった。それに、自分で危なそうなパターンを見つける必要があるのでめんどくさい
- 想定解法の場合、文字列が一意に定まるのがいい感じ。反転したら一意になるとか気づけねーよって感じ。
- 文字列を反転したら気づきを得るかもしれないっていうのは頭の片隅にでも置いておく。
- DP解法については、DPってこんなところでも使えるんだーって思った。なんかDPの使い時がまだ分かってない。
ABC050 「Lining Up」
考察と解法
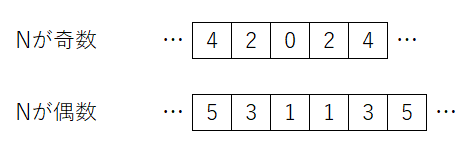
- Nが奇数の時と偶数の時で、何番が何回出てくるかは決まっている。
- なので、まずは入力配列に間違いがないかを確認する。間違いがあれば答えは0となる。
- 間違いがなかった場合、$2^{\lfloor \frac{N}{2} \rfloor}$が答えとなる。配列において、同じ数字が登場する回数は$\lfloor \frac{N}{2} \rfloor$回なので。
コード
# include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll MOD = 1e9+7;
int N;
int a[111111]; // 入力配列
int v[111111]; // v[i]: 入力配列中にiがいくつあるか
// 2^x乗を計算
ll calc(ll x) {
ll ret = 1;
while (x > 0) {
ret = ((ret%MOD) * (2%MOD)) % MOD;
x--;
}
return ret;
}
int main() {
cin >> N;
for (int i = 0; i < N; i++) {
cin >> a[i];
v[a[i]]++;
}
bool ok = true;
// Nが奇数か偶数かで場合分け
if (N&1) {
if (v[0] != 1) ok = false;
for (int i = 2; i < N; i+=2) {
if (v[i] != 2) ok = false;
}
} else {
for (int i = 1; i <= N; i+=2) {
if (v[i] != 2) ok = false;
}
}
if (ok) {
cout << calc(N/2) % MOD << endl;
} else {
cout << 0 << endl;
}
return 0;
}
- コンテスト中はクソコードを書いてしまったためリファクタリングした。
感想
- コンテスト中にきれいに実装するの難しいね...
