はじめに
numpyやpytorchを使っていると、頻繁に3次元以上の配列に遭遇しますよね。
人間の頭では、3次元以上を想像するのはとても難しいです。
その一方で、どんな多次元配列でも、所詮はメモリ上に一列に並んでいます。
それを多次元配列を使って、我々がアクセスしているだけ、と考えればそれほど怖くなくなります。
これを意識すると、ブロードキャストとかも、直感的に理解できますし、
なぜブロードキャストできない場合があるのかも、理解できます。
(よくshapeが悪い!とエラーで怒られても、それほど焦らずに済みます。)
メモリ配置
まず1次元配列
import numpy as np
np.random.rand(3)
# >> array([0.67531291, 0.39123613, 0.65122989])
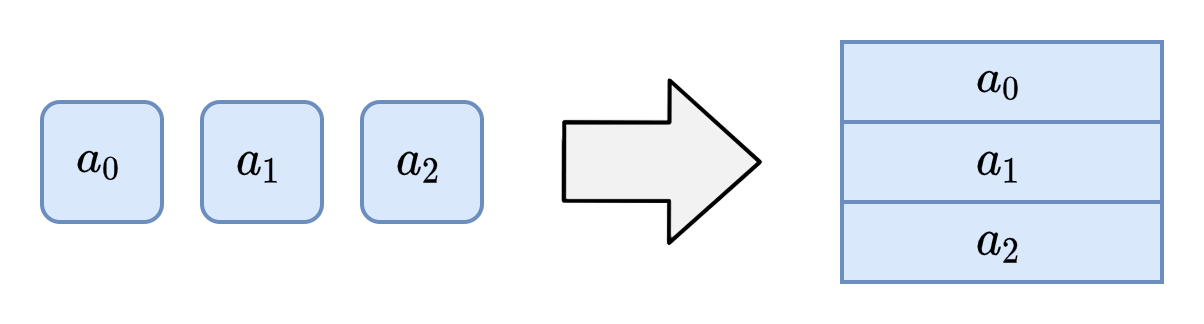
1次元配列は、そのままの順番で一列に並びます。
基本ですが、一つ要素を移動すると、アドレスが一つずれます。
2次元配列(行列)
import numpy as np
np.random.rand(3,3)
# >> array([[0.23131406, 0.80539163, 0.72888864],
# >> [0.30545592, 0.1298448 , 0.51332658],
# >> [0.39577805, 0.27866544, 0.52592152]])
2次元配列は、まず横方向の要素がメモリ上に並べられ、
その次に、次の行のデータが並べられます。
添え字の最も右側をインクリメント(横移動)すると、アドレスが一つずれます。
添え字の右から2番目をインクリメント(縦移動)すると、アドレスが横要素の個数分ずれます。

3次元配列
import numpy as np
np.random.rand(3,3,3)
# >> array([[[0.25302496, 0.42355715, 0.5267075 ],
# >> [0.5960759 , 0.95850513, 0.95984181],
# >> [0.87569986, 0.92117938, 0.50016966]],
# >>
# >> [[0.24515091, 0.87402237, 0.65732351],
# >> [0.40590343, 0.27378174, 0.16059929],
# >> [0.61030218, 0.97677065, 0.99856145]],
# >>
# >> [[0.96181558, 0.06190622, 0.57253151],
# >> [0.21805162, 0.88300779, 0.77791324],
# >> [0.455423 , 0.63827398, 0.90376446]]])
3次元配列は、このように並べられます。
添え字の最も右側をインクリメント(横移動)すると、アドレスが一つずれます。
添え字の右から2番目をインクリメント(縦移動)すると、アドレスが横要素の個数分ずれます。
添え字の右から3番目をインクリメントすると、アドレスが横要素x縦要素の個数分ずれます。

このように、添え字が左に行くに従い、メモリを大きく移動します。
4次元配列
4次元以上も基本的には、同じ構成になります。
図示することは難しいですが、メモリ上は一列に並んでいるだけとなります。
よくあるデータ構造の例としては、以下のようなshapeのものがありますね。
shape = (バッチ数, バッチサイズ, RGBチャネル数(3), 縦画素数, 横画素数)
# shape = (バッチ数, バッチサイズ, 縦画素数, 横画素数, RGBチャネル数(3)) # RGBの場所は一番右の場合もある
演算上、まとめて使う可能性のある成分は、右側の要素に置いておく方が、
メモリ上近くに並ぶため、計算上効率が良いです。
例えば、画素間でしかConvolutionをしない場合は、画素情報成分を右側に、
チャネル間でしかConvolutionをしない場合は、チャネル成分を右側に持ってきた方がよいです。
また、pytorchにreshape, view + contiguousがあるのは、ここら辺のメモリ配置が関係しています。
集約のaxisとの関係
numpyの集約(sumやmeanなど)するときに指定するaxisは、
axis=0の時には最も左側のメモリ的に遠い成分の添え字が集約されます。
(分かりやすさのため、keepdims=Trueにして演算した例を示します)
A = np.random.rand(3,3,3)
A.shape
# >> (3, 3, 3)
A.sum(axis=0, keepdims=True).shape
# >> (1, 3, 3)
A.sum(axis=1, keepdims=True).shape
# >> (3, 1, 3)
axisのない集約をどう計算するか
W.I.P.
ブロードキャストについて
W.I.P.