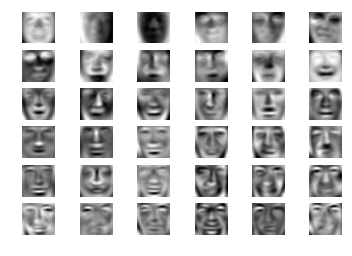Coursera Machine Learningの課題をPythonで: ex7-2 (主成分分析) #Python

はじめに

機械学習を学ぶ第一歩として定番のCourseraのMachine Learningコース（Stanford、Andrew Ng先生）。このコースのMatlab/Octaveのプログラミング課題をPythonで実装するシリーズ。
今回はex-7 教師なし学習の後半、主成分分析(Principal Component Analysis, PCA)をやります。

ライブラリのインポート

各種ライブラリをインポートします。

import numpy as np
import scipy.io as scio
import matplotlib.pyplot as plt
from sklearn import decomposition

データの読み込み・表示

Matlabの.mat形式のデータをscipy.io.loadmat()で読み込みます。データは32x32ピクセルの256階調グレースケール画像が5000枚。5000x1024の2次元行列に入ってきます。
これをとりあえずそのまま表示（最初の100画像だけ）してみます。

data = scio.loadmat('ex7faces.mat')
X = data['X'] # Xは5000x1024の2次元行列

fig = plt.figure()
plt.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=None, hspace=None)
for i in range(0,100):
    ax = fig.add_subplot(10,10,i+1)
    ax.axis('off')
    ax.imshow(X[i].reshape(32,32).T, cmap = plt.get_cmap('gray'))
plt.show()

出力はこちら。

主成分分析の実施

32x32ピクセル = 1024次元で表現されている元画像データに主成分分析をかけることによって、100次元までデータを縮減します。主成分分析は sklearn.decomposition.PCA()クラス一発です。パラメータn_components= でいくつまで主成分を取るかを指定できます。

pca = decomposition.PCA(n_components=100)
pca.fit(X)

主成分の可視化

主成分分析の結果は、pca.components_に格納されています。100x1024の2次元行列です。この主成分ベクトルをそのまま表示することができます。最初の36主成分だけ表示してみましょう。

fig = plt.figure()
plt.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=None, hspace=None)
for i in range(0,36):
    ax = fig.add_subplot(6,6,i+1)
    ax.axis('off')
    ax.imshow(pca.components_[i].reshape(32,32).T, cmap = plt.get_cmap('gray'))
plt.show()

結果はこちら。

次元縮減と再構築

主成分分析は、もともと1024次元ベクトルで表現されていた画像情報を、100次元まで縮減していることになります。次元縮減したデータセットは、pca.transform(X)で取得することができます（5000x100の2次元ベクトル）。
これに主成分ベクトルを掛けて、5000x1024の2次元ベクトルを復元します。復元したデータは、元データを100の主成分で圧縮して、表示できるように復元したものとなります。再構築した結果の最初の100個の画像を表示してみます。

Xreduce = pca.transform(X) # 次元縮減。結果は5000x100行列
Xrecon = np.dot(Xreduce, pca.components_) # 再構築。結果は5000x1024行列

fig = plt.figure()
plt.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=None, hspace=None)
for i in range(0,100):
    ax = fig.add_subplot(10,10,i+1)
    ax.axis('off')
    ax.imshow(Xrecon[i].reshape(32,32).T, cmap = plt.get_cmap('gray'))
plt.show()

結果はこちら。上にある元画像と比べると、ディテールは失われているものの、おおまかな特徴は復元されているのがわかります。

おわりに

今回もシンプルなコードになりました。