Coursera Machine Learningのプログラミング課題をPythonで実装するシリーズ。
(2015/10/23) ex2_regを追加し、追記。
(2015/12/25) ex2_regでPolynomialFeaturesを使って簡単に書く版を追記
ex2 (正則化なしロジスティック回帰)
はじめに
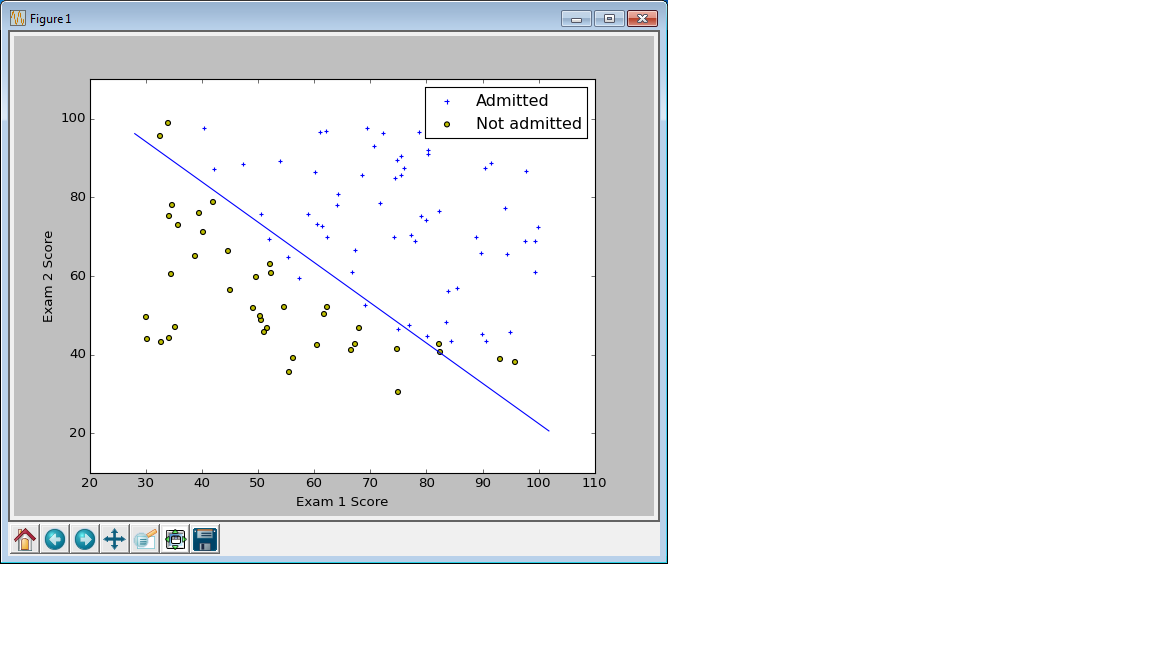
この例題では、2つのテストの点数が入力データ、テストの結果(合格 or 不合格)が出力データとして与えられ、ロジスティック回帰による分類器を作成する。
Pythonコード
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model
data = pd.read_csv("ex2data1.txt", header=None)
# read 1st, 2nd column as feature matrix (100x2)
X = np.array([data[0],data[1]]).T
# read 3rd column as label vector (100)
y = np.array(data[2])
# plot
pos = (y==1) # numpy bool index
neg = (y==0) # numpy bool index
plt.scatter(X[pos,0], X[pos,1], marker='+', c='b')
plt.scatter(X[neg,0], X[neg,1], marker='o', c='y')
plt.legend(['Admitted', 'Not admitted'], scatterpoints=1)
plt.xlabel("Exam 1 Score")
plt.ylabel("Exam 2 Score")
# Logistic regression model with no regularization
model = linear_model.LogisticRegression(C=1000000.0)
model.fit(X, y)
# Extract model parameter (theta0, theta1, theta2)
[theta0] = model.intercept_
[[theta1, theta2]] = model.coef_
# Plot decision boundary
plot_x = np.array([min(X[:,0])-2, max(X[:,0])+2]) # lowest and highest x1
plot_y = - (theta0 + theta1*plot_x) / theta2 # calculate x2
plt.plot(plot_x, plot_y, 'b')
plt.show()
機械学習的ポイント
ロジスティック回帰をするにはsklearn.linear_model.LogisticRegression()クラスを利用し、おなじみのmodel.fit(X,y)で学習する。
LogisticRegressionクラスでは、Regularization(正則化)の強さをパラメータCで指定する。授業ではこれをパラメータ$\lambda$で指定していたが、Cは$\lambda$の逆数という関係(後のSVMのセッションで出てくる)。Cが小さいほど正則化を強く、大きいほど正則化を弱くすることができる。この例題では正則化なしにしたいため、Cには大きな値(1,000,000)を入れた。
モデルを学習した後は、Decision Boundary(決定境界)を描画する。ロジスティック回帰の決定境界は $\theta^{T} X = 0$で定義される直線。例題の場合、成分で書き下すと、$\theta_0 + \theta_1 x_1 + \theta_2 x_2 = 0$、これを解いて $x_2 = - \frac{\theta_0 + \theta_1 x_1}{\theta_2}$ の式で決定境界上の点の座標を計算し、plot関数に渡す。
Python的ポイント
- y=1のものを+、y=0のものを○で散布図にプロットする際に、Numpyのブールインデックス(論理値によるインデックス)を使っている。
- 決定境界(直線)をプロットする際に、直線の両端の点を成分に持つ2次元のベクトルを
plot_xに入れ、それに対応するplot_yをベクトル演算している。このplot_xを作る際に、Numpy Arrayとして作成しないと(Python標準のリストとして作成してしまうと)、ベクトル演算ができないので注意。
ex2_reg(正則化ありロジスティック回帰)
はじめに
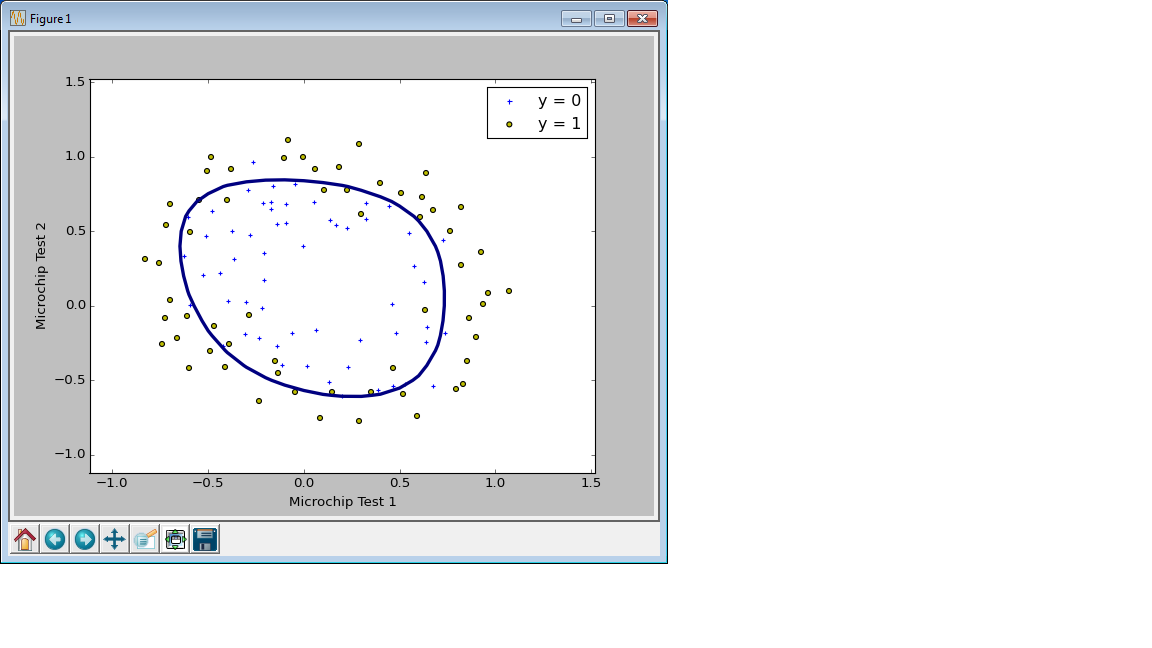
この例題では、マイクロチップの2つのテスト結果が入力データ、合格or不合格のフラグが結果データとして与えられる。ロジスティック回帰モデルを用いて合格と不合格を分類する分類器を作成する。直線で線形分離できないため、多項式によるあてはめを使用する。また、異なる正則化パラメータ$\lambda$でモデルを作成し、正則化の効果をみる。
コード
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model
# mapFeature(x1, x2)
# feature mapping(特徴量マッピング)をする
# 引数:特徴量ベクトル x1, x2 (同じ次元nでなければならない)
# 返り値:特徴量行列 X (nx28行列)
# 6次までの場合 1, x1, x2, x1^2, x1*x2, x2, x1^3, .... x1*x2^5, x2^6 のように28列になる
def mapFeature(x1, x2):
degree = 6
out = np.ones(x1.shape) # 最初の列は 1
for i in range(1, degree+1): # 1 から degree までループ
for j in range(0, i+1): # 0 から i までループ
out = np.c_[out, (x1**(i-j) * x2**j)] # 列を増やしていく
return out
# ここから本文
data = pd.read_csv("ex2data2.txt", header=None)
x1 = np.array(data[0])
x2 = np.array(data[1])
y = np.array(data[2])
# サンプルデータをプロットする
pos = (y==1) # numpy bool index
neg = (y==0) # numpy bool index
plt.scatter(x1[pos], x2[pos], marker='+', c='b') # 正例は'+'
plt.scatter(x1[neg], x2[neg], marker='o', c='y') # 負例は'o'
plt.legend(['y = 0', 'y = 1'], scatterpoints=1)
plt.xlabel("Microchip Test 1")
plt.ylabel("Microchip Test 2")
# 特徴量マッピングをする Xはnx28行列
X = mapFeature(x1, x2)
# Logistic regression model 正則化あり
model = linear_model.LogisticRegression(penalty='l2', C=1.0)
model.fit(X, y)
# Decision Boundary(決定境界)をプロットする
px = np.arange(-1.0, 1.5, 0.1)
py = np.arange(-1.0, 1.5, 0.1)
PX, PY = np.meshgrid(px, py) # PX,PYはそれぞれ 25x25 行列
XX = mapFeature(PX.ravel(), PY.ravel()) # 特徴量マッピング。引数はravel()で625次元ベクトルに変換して渡す。XXは 625x28行列
Z = model.predict_proba(XX)[:,1] # ロジスティック回帰モデルで予測。y=1の確率は結果の2列目に入っているので取り出す。Zは625次元ベクトル
Z = Z.reshape(PX.shape) # Zを25x25行列に変換
plt.contour(PX, PY, Z, levels=[0.5], linewidths=3) # Z=0.5の等高線が決定境界となる
plt.show()
機械学習的ポイント
LogisticRegressionクラスを使う部分は先の例題と同じ。Courseraで出てきたRegularization(正則化)はL2正則化(リッジ回帰)なので、'penalty='l2'のオプションを入れる。
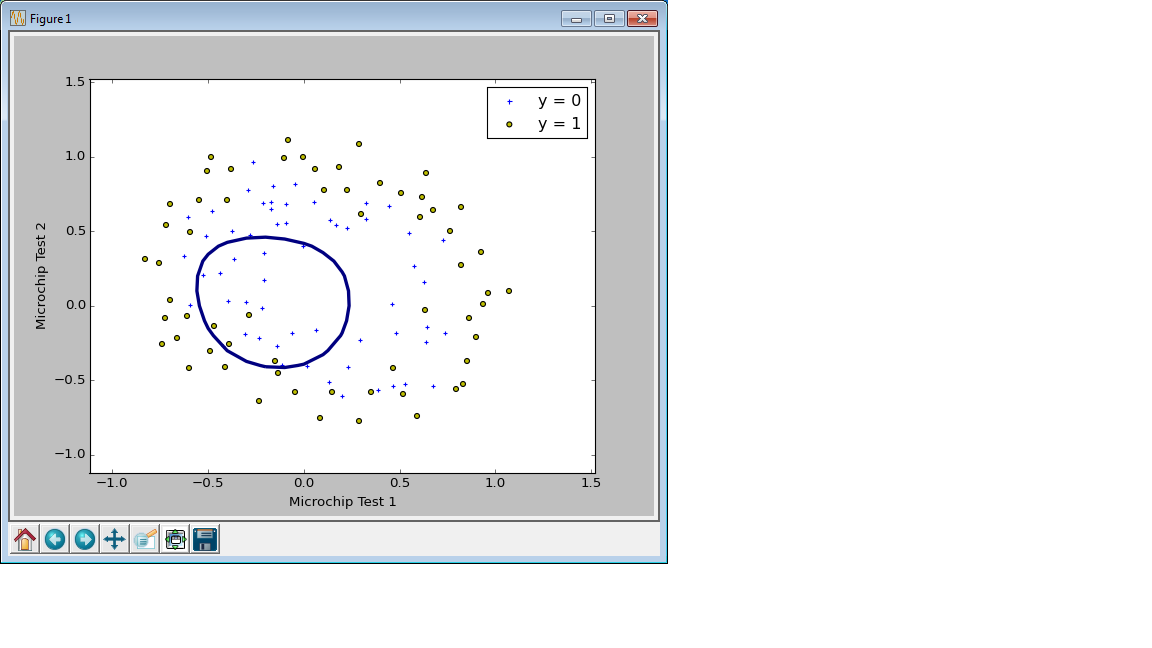
正則化の強さを変えて学習をしたモデルで決定境界を描いてみるが、Courseraでは$\lambda = 0, 1, 100$の3種類だったところを、Pythonの例ではC=1000000.0,C=1.0,C=0.01として描いてみた。
C=1000000.0の場合 (正則化なし、オーバーフィット)
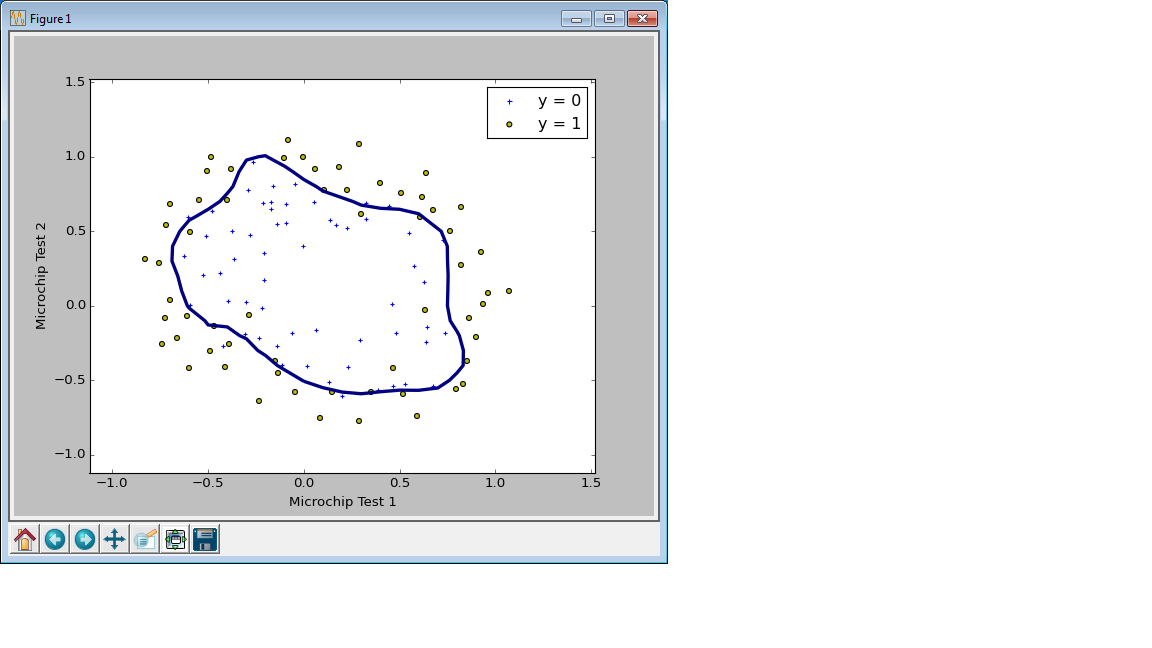
Python的ポイント
-
ravel()メソッドで行列をベクトルに変換する。Matlab/OctaveではA(:)に対応。meshgridで作成した座標の行列は、mapFeatureやLogisticRegression.predict_proba()に渡す際にはベクトルにする必要があるため。逆に、返り値のベクトルZはreshape()メソッドで行列にもどす。 -
LogisticRegression.predict_proba()の返り値は縦がサンプル数(625行)、横がクラス数(2列)の行列で、各サンプルが各クラスに分類される確率が入っている。この例題では欲しいのはy==1となる確率なので、Z[:,1]として2列目のみをベクトルとして取り出す。確率=0.5の等高線が、決定境界となる。
追記:多項式の特徴量生成にライブラリを使って簡略化
上記コードでは、多項式の特徴量の生成のためにmapFeature()という関数を自作していたが、scikit-learnにはsklearn.preprocessing.PolynomialFeaturesという同じことをしてくれるクラスがあるため、こちらで置き換える。コードはこちら。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import sklearn
data = pd.read_csv("ex2data2.txt", header=None)
x1 = np.array(data[0])
x2 = np.array(data[1])
y = np.array(data[2])
# サンプルデータをプロットする
pos = (y==1) # numpy bool index
neg = (y==0) # numpy bool index
plt.scatter(x1[pos], x2[pos], marker='+', c='b') # 正例は'+'
plt.scatter(x1[neg], x2[neg], marker='o', c='y') # 負例は'o'
plt.legend(['y = 0', 'y = 1'], scatterpoints=1)
plt.xlabel("Microchip Test 1")
plt.ylabel("Microchip Test 2")
# 特徴量マッピングをする Xはnx28行列
poly = sklearn.preprocessing.PolynomialFeatures(6)
X = poly.fit_transform(np.c_[x1,x2])
# Logistic regression model 正則化あり
model = linear_model.LogisticRegression(penalty='l2', C=1.0)
model.fit(X, y)
# Decision Boundary(決定境界)をプロットする
px = np.arange(-1.0, 1.5, 0.1)
py = np.arange(-1.0, 1.5, 0.1)
PX, PY = np.meshgrid(px, py) # PX,PYはそれぞれ 25x25 行列
XX = poly.fit_transform(np.c_[PX.ravel(), PY.ravel()]) # 特徴量マッピング 引数はravel()で625次元ベクトルに変換して渡す XXは 625x28行列
Z = model.predict_proba(XX)[:,1] # ロジスティック回帰モデルで予測 y=1の確率は結果の2列目に入っているので取り出す Zは625次元ベクトル
Z = Z.reshape(PX.shape) # Zを25x25行列に変換
plt.contour(PX, PY, Z, levels=[0.5], linewidths=3) # Z=0.5の等高線が決定境界となる
plt.show()
おわりに
Python、機械学習ともに勉強中ですのでおかしな所ありましたらご指摘くださると嬉しいです(^^)