この記事の方針
シオドア・スタージョンは「SFの90%はクズである──ただし、あらゆるものの90%はクズである」と言いましたが、ご多分にもれず公開鍵暗号関係の書籍・技術記事も90%はクズであることは有名です。
特に「電子署名はハッシュ値を秘密鍵で暗号化~」とか「SSL/TLSは共通鍵を公開鍵で暗号化~」みたいな誤った説明が蔓延していることはご存じの方が多いと思います。
では、何故そのような誤った説明が蔓延しているのでしょうか。一つの理由は、「機能や使い方だけではなく、仕組みを(せめて雰囲気だけでも)知らなければ、理解したとは言えない」という思い込みではないでしょうか?
「秘密鍵で暗号化」などの誤った説明は、分かりやすくて「仕組みを雰囲気だけでも知りたい」という人にとっては満足行く説明です。実際には『本当の仕組み』とは大きく異なっているにもかかわらず、「ああ、これが電子署名の仕組みなのか」と納得してしまいます。
そこで本記事では、別のアプローチで『仕組み』を雰囲気だけでも伝えることはできないか、と考えました。読んだ人が、「ああ、これは『本当の仕組み』とは違うのだけれど、でも『本当の仕組み』もこれと似たようなものなんだろう」という形で納得感を得られるものを目指しました。
それでは、本文をお読みください。
はじめに ~足し算だけの世界
ここは足し算だけの世界。この世界には、「計算」は足し算しかありません。1 掛け算も引き算も、ましてや累乗もありませんが、それでも人々は平和に暮らしていました。
足し算はあるわけですから、たとえば「7 と 8 を足した数はいくら?」という質問にはこの世界でも簡単に答えられます。
では、「8 を足すと 15 になる数はいくら?」という質問にはこの世界では答えられるでしょうか?
我々の世界であれば、式変形して
\begin{align}
★+8 &= 15\\
★ &= 15-8\\
&=7
\end{align}
と簡単に答えを求められます。ですがここは「足し算だけの世界」、引き算は存在しないのでこうした計算はできません。では、この世界ではこの質問には答えられないのでしょうか?
いいえ、このようにしてやれば答えを求めることができます。
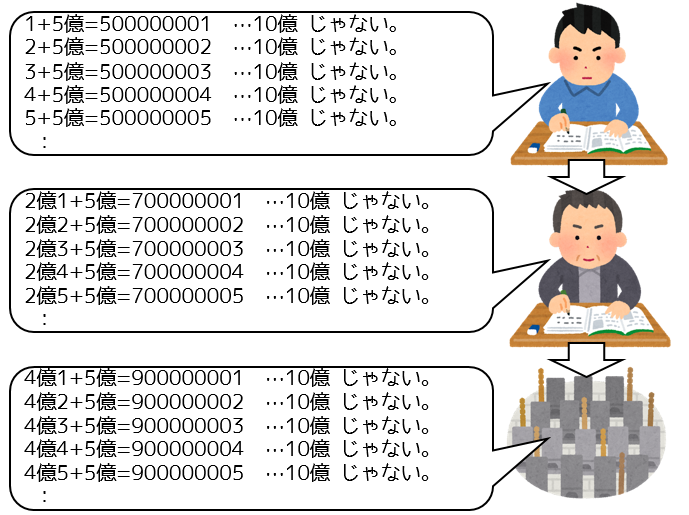
しかし、これは明らかに大変な作業です。「8 を足すと 15 になる数はいくら?」くらいならいいですが、「5億を足すと10億になる数はいくら?」という質問にこの方法で答えようとすると、膨大な時間が必要になってしまいます。
つまりこの世界の特徴をまとめると、このようになります。
| ★と▲を足した数はいくら? | ★を足すと▲になる数はいくら? |
|---|---|
| 簡単に計算できる。 | 簡単には計算できない。 特に数が大きい場合は、事実上計算不可能。 |
では、そんな世界の物語です。
アリスとボブと、暗黒郵政公社
アリスとボブは文通をしていました。
二人は住んでいるところが遠いため一度も会ったことはありませんが、だからこそ身近な友人には逆に話せないような悩みもお互いに打ち明け合うことができました。家族のこと、将来のこと、生きる意味について、自分の心の中にある闇について、神は実在するのか?理想郷とは何か?…アリスとボブの文通は、そうした他人には知られたくない話題がたくさんやり取りされていたのです。
しかし、そんな二人の平穏な日々に危機が訪れます。悪の秘密結社が郵政公社を乗っ取り暗黒郵政公社と化してしまったのです。
暗黒郵政公社は新事業を立ち上げました。郵便物の盗み見による脅迫事業です。
これでは今までのように、安心して秘密を文通で伝えることができません。アリスは途方に暮れてしまいました。
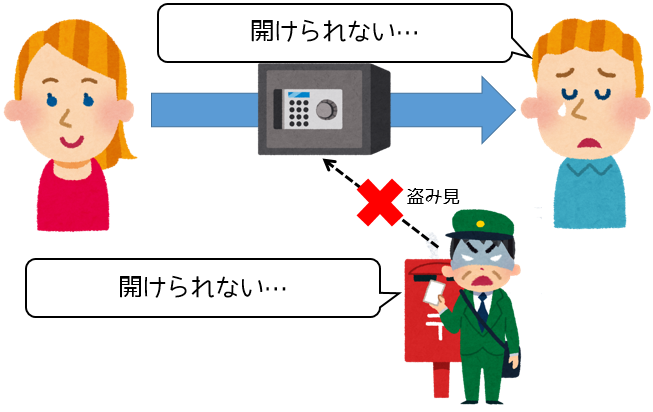
そんなある日、雑貨屋でアリスは良いものを見つけました。任意の番号で鍵をかけることのできる丈夫な箱です。
この箱に手紙を入れて鍵をかけてしまえば、暗黒郵政公社といえども盗み見はできないに違いありません。2
しかし箱を買っていざボブに手紙を送ろうとした時、アリスは大きな問題に気づきます。たしかに暗黒郵政公社といえども番号がわからないことには開けることはできないでしょうが、それはボブも同様です。なんとかしてボブに番号を伝えなければ、文通を行うことができないのです。
ですが、どうやってボブに番号を伝えればいいのでしょうか?この世界には電話やSNSといった通信手段はまだ無いので、アリスとボブのように遠く離れた二人がやり取りする手段は郵便しかありません。しかし郵便を使ってボブに番号を伝えてしまったら、暗黒郵政公社にその番号を盗み見され、その後鍵をかけて手紙をやり取りしようが暗黒郵政公社はその鍵を開けることができてしまいます。
アリスは悩んだ末、ついにこの問題を解決する秘奥義を編み出しました。アリスは、この秘奥義を「で(De)きた…この方(Hou)法なら安全に鍵番号を共有できるわ!」、略して「DH鍵共有」と名付けました。では、この秘奥義:DH鍵共有の中身を見てみましょう!
鍵共有
鍵共有は、その名の通り同じ鍵番号をアリスとボブで共有する方法です。しかしどうすれば、暗黒郵政公社に知られることなく同じ鍵番号を共有できるのでしょうか?
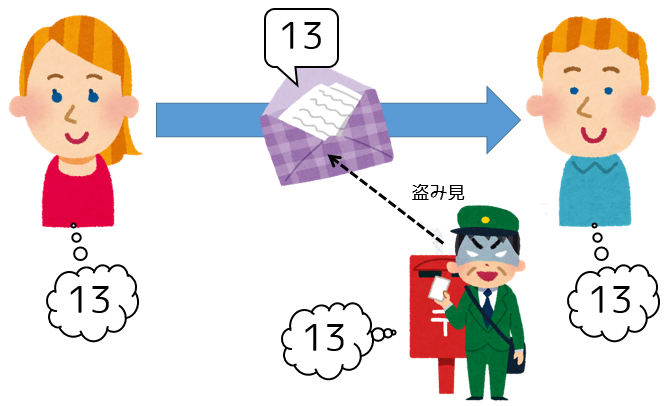
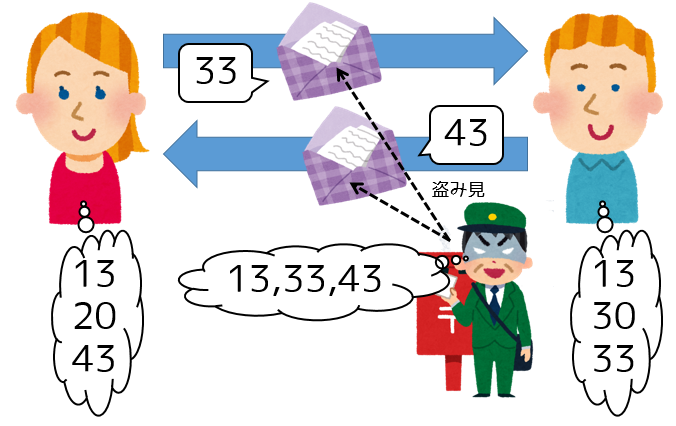
まず、アリスがボブに適当な数値(仮にこれを「初期数」と呼ぶことにします。別にボブがアリスに送るのでも構いません。)、たとえば「13」を郵便で送ります。(説明を簡単にするため小さめの数値にしていますが、実際にはもっと大きな数値にします。以後の数も同様です。)もちろんこの郵便自体には鍵がかかっていないので、暗黒郵政公社もこの「13」という数を知ることができてしまいます。
続いて、アリスとボブはそれぞれ適当な数値(これを仮に、「アリスの/ボブの秘密数」と呼ぶことにします。)を決めます。たとえばアリスは 20 、ボブは 30 を自分の秘密数にしたとしましょう。そうしたら、さきほどの初期数「13」に自分の秘密数を足した数(これを仮に、「アリスの/ボブの公開数」と呼ぶことにします。)を計算します。この例であれば、アリスの公開数は「13+20=33」、ボブの公開数は「13+30=43」です。
そうしたら、アリスとボブはお互いに自分の公開数「33」「43」を送りあいます。もちろんこの数値も、暗黒郵政公社は知ることができてしまいます。
相手の公開数を受け取ったら、それに自分の秘密数を足します。アリスの場合、ボブの公開数 43 に自分の秘密数 20 を足して 63。ボブの場合、アリスの公開数 33 に自分の秘密数 30 を足して、63 …なんと、二人の計算結果がピッタリ一致しました。これはちょっと考えてみると当たり前です。
- 「ボブの公開数43」=「初期数13」+「ボブの秘密数30」
- 「アリスの公開数33」=「初期数13」+「アリスの秘密数20」
なので、「ボブの公開数43」+「アリスの秘密数20」も「アリスの公開数33」+「ボブの秘密数30」も、どちらも同じ「初期数13」+「アリスの秘密数20」+「ボブの秘密数30」になるからです。あとはこの数値を鍵番号として使えば、二人とも鍵の開け閉めができるようになります。
一方、暗黒郵政公社の側は「初期数13」「アリスの公開数33」「ボブの公開数43」の 3 つを盗み見ることができていますが、この 3 つをどのように足しても「63」を得ることはできません。これが我々の世界であれば「アリスの公開数33」と「初期数13」から引き算を用いて「アリスの秘密数20」を求めて最終的には「63」を得ることができますが、最初に説明したとおりこの「足し算だけの世界」ではそれは困難です。数が充分大きければ、暗黒郵政公社が鍵番号を知ることは実質不可能になります。
このDH鍵共有によって、アリスとボブは暗黒郵政公社に知られることなく秘密をやり取りすることができるようになったのです。
次回予告
こうして再び平穏な文通生活を取り戻したアリスとボブ。しかし、二人の前にまたも暗雲がたちこめます。暗黒郵政公社はさらなる新事業「改竄・なりすまし事業」に手を染めようとしているのです。
はたしてアリスとボブに平和は訪れるのか?次回「デジタル署名」、乞うご期待!
解説
この「足し算だけの世界」では、「足し算」は容易にできるが「逆の計算」(引き算)は事実上不可能…という性質を利用して、「鍵共有」をすることに成功しました。
我々の住むこの世界では足し算の逆の計算は簡単にできてしまいますから、当然この方法では鍵共有はできません。しかし「ある計算」は容易だが その「逆の計算」は困難…という計算がいくつかあり、それを利用することで同様に鍵共有を行うことが可能です。
代表的なものとしては、離散対数があります。「★を▲乗して、■で割った余り」は容易に求められますが、「★を何乗したら、■で割った余りが△になるか?」を求めるのは(数が大きい場合には)困難です。この性質を利用した鍵共有として、ディフィー・ヘルマン鍵共有 があります。