Intro
-
近年どんどんとモデルサイズが大きくなるにつれて,計算効率・エナジー効率の良いモデルの必要性が増している.
-
Spiking Neural Networks (SNN)は情報をバイナリのスパイク列で表現する.これを,スパイクが来た時だけ動くevent-drivenなハードウェア(neuromorphic chips)で動かせば,高いエナジー効率を実現できると言われている.
-
SpikeGPTでは,言語生成にSNNを用いた.ただし,(多くのSNN研究がそうであるように)SNNなのはモデルの一部のみで,モデルの大部分は普通に連続値を扱う.
- SNNのみで実用的なパフォーマンスのモデルを実装することはまだまだ難しい.
構造
-
Transformerと見比べれば,GPTのMulti-Head AttentionをSpiking RWKVで,Feed ForwardブロックをSpiking RFFNというものでそれぞれ置き換えたということがわかる.
- RWKV (Receptance Weighted Key Value)は元々計算・メモリ効率の良いself-attentionの代替として提案された.Recurrentなself-attentionのようなもので,本論文ではこれをserializeしてスパイキングニューロンに入力できるような形に書き換えたのが要点の一つ.
Binary Embedding
-
SNNで扱うため,連続値の単語埋め込みベクトルをバイナリ列に変換する必要がある.これにはヘヴィサイド関数を用いた.
-
ヘヴィサイド関数は非連続で微分不可のため,近似的な勾配を伝えるため逆伝播ではこれを$\arctan$で置き換えた:
\begin{align}
& \sigma(x) = \frac{1}{\pi} \arctan(\frac{\pi}{2} \alpha x) + \frac{1}{2} \\
& \sigma'(x) = \frac{\alpha}{2(1 + (\frac{\pi}{2} \alpha x)^2)}
\end{align}
※ 割と明らかですが,論文で$\sigma'(x) = \frac{1}{\pi} \arctan (\pi x) + \frac{1}{2}$となっているのは誤植だと著者に伺いました.また,ハイパラ$\alpha$などを加えたrefined versionをいただいたので記載しています.
Token-shift
- Spiking RWKVとSpiking RFFNの前にあるもの.名のとおり,入力$X$のトークンをシフトしたもの$X_s$を,$X$に重みづけて足す.
\begin{align}
& X_s = ZeroPad_{[0, 0, -1, 1]}(X) \\
& W_{shift} = [(\frac{i}{E})^{n/N}], \quad i=1, ..., E \\
& \chi = W_{shift} \odot X + (1 - W_{shift}) \odot X_s
\end{align}
- モデルが過去の文脈情報に注目しやすくする点で,induction headのアイディアに似ている.
実装
def token_shift(x: np.ndarray, n: int, N: int) -> np.ndarray:
"""
Args:
x: ( E, T ) where E is the embedding size of each token and T is time
n: current block
N: total number of blocks
Returns:
chi: ( E, T ) | token shifted input X
"""
# NOTE: np.pad doesn't accept negative padding
x_s = np.pad(x[:, 1:], ((0, 0), (0, 1)), mode='constant', constant_values=0) # ( E, T )
E = x.shape[0]
w_shift = (np.arange(1, E + 1) / E) ** (n / N) # ( E, )
w_shift = w_shift.reshape(-1, 1) # ( E, 1 )
return w_shift * x + (1 - w_shift) * x_s, w_shift.squeeze()
-
ブロック数$N=5$で乱数を入れ可視化.
-
ブロックが進むほど$X$と$X_s$を混ぜる割合が線型になっていく.(割合が0.5になる次元で最もぼやけて見えている)
Spiking RWKV
RWKV (Receptance Weighted Key Value)
-
RWKVは,メモリ効率の良いself-attentionの代替として提案された.推論時はRNNに似てトークンを逐次的に入れて一つの隠れ状態をアップデートしていく一方,訓練時はTransformerのように時間方向に並列化する.
-
まず,モジュールへの入力(今回の場合Token shiftされた$\chi$)を3つの線形層で変換するところはself-attentionと同じ.
- Query $Q$はなく,代わりにreceptance matrix $R$というものがある.$R$は$T$方向における過去の情報をどれだけ利用するかをゲーティングする.
\begin{align}
& R = \chi^\top M_R \quad K = \chi^\top M_K \quad V = \chi^\top M_V \\
& \chi \in \mathbb{R}^{E \times T} \quad {M_R, M_K, M_V} \in \mathbb{R}^{E \times H} \quad {R, K, V} \in \mathbb{R}^{T \times H}
\end{align}
以上$R, K, V$を用いて,$Y$を計算する:
Y_t = \sigma(R_t) \odot \frac{\sum^t_{i=1}\exp(W_{i-t-1}) \odot \exp{(K_i)} \odot V_i}{\sum^t_{i=1}\exp(W_{i-t-1}) \odot \exp{(K_i)}}
-
$R$と$W$と$K$の積が$V$の要素を重みづけるもの(matching degree)になっていると読み取れる.(self-attentionにおける$Q$と$K$の行列積に対応)
- $W$ (positional weight bias)は学習可能ではない.計算方法はかなり恣意的に決められるようだが(詳細は論文),時間方向に減衰していく$\mathbb{R}^{E \times T}$であれば割と色々試せそう.
-
$Y$は$t$が増えるにつれ,より長い過去の情報を見ることになる.
※ 論文中$W_{(T-i+1)}$の$T$はおそらく$t$の誤り.また,多分マイナスをつけて$W_{(i-t-1)}$にしないとインデックスが合わない.(こちらは著者に確認取ってませんが,RWKVの説明を参照)
実装
- 本来${R, W, K, V, Y} \in \mathbb{R}^{T \times H}$のはずだが,論文で$E = H$としているので${R, W, K, V, Y} \in \mathbb{R}^{T \times E}$
def sigmoid(x: np.ndarray) -> np.ndarray:
return 1 / (1 + np.exp(-x))
def vanilla_rwkv(r: np.ndarray, w: np.ndarray, k: np.ndarray, v: np.ndarray) -> np.ndarray:
"""
Args:
r: ( T, E ) where E is the embedding size of each token and T is time
w: ( T, E ) weights for each time step
k: ( T, E ) keys
v: ( T, E ) values
Returns:
y: ( T, E )
"""
T = r.shape[0]
y = []
for t in range(1, T + 1):
# NOTE: change indexing to T - i - 1 to match the paper
values = np.sum([np.exp(w[i - t - 1]) * np.exp(k[i - 1]) * v[i - 1] for i in range(1, t + 1)])
norm = np.sum([np.exp(w[i - t - 1]) * np.exp(k[i - 1]) for i in range(1, t + 1)])
y_t = sigmoid(r[t - 1]) * values / norm
y.append(y_t)
return np.stack(y)
Serialized RWKV
- RWKVを時間方向に連続して計算するものにすることで,その出力をstep by stepでLIFニューロンに渡すことができる.
\begin{align}
Y[t+1] &= \sigma (RY[t]) \cdot \frac{\exp (KY[t]) \cdot (VY[t]) + \exp(W) \cdot A[t]}{\exp(KY[t]) + \exp(W) \cdot B[t]} \\\\
A[t] &= \exp(KY[t-1]) \cdot (VY[t-1]) + \exp(W) \cdot A[t-1] \\
B[t] &= \exp(KY[t-1]) + \exp(W) \cdot B[t-1]
\end{align}
※ 論文の式(10)-(12)に相当するところですが,次のバージョンでrefineしてくれるそうです.今のバージョンではserialized RWKVの導出もなく,$A[0]$や$B[0]$の計算方法も不明...
※ あと多分式(10)の$\sigma(RX[t])$は$\sigma(RY[t])$の誤り.
Leaky Integrated-and-Fire neuron
※ このLIFの表記がおかしいと思い書き直しました.こちらも著者に確認とっておらず後ほど要確認です.
\begin{align}
& U[t] = H[t-1] + \beta(Y[t] - (H[t - 1] - U_{reset})) \\
& S[t] = \Theta (U[t] - U_{threshold}) \\
& H[t] = U[t] \cdot (1 - S[t]) + U_{reset} \cdot S[t]
\end{align}
- $U$: LIFニューロンの膜電位(機械学習ではただhidden stateと考えた方が自然)
- $U_{threshold}$: LIFニューロンの閾値(これを超えるとスパイクを発する)
- $U_{reset}$: LIFニューロンのリセット電位(スパイクを発した直後この膜電位に戻る)
- $S$: バイナリのスパイク列
- $\Theta$: ヘヴィサイド関数
- $H$: 発火後リセット電位に戻すためのフィードバック
- $Y$: LIFニューロンへの入力(今回の場合serialized RWKVの出力)
- $\beta$: 減衰率(膜時定数の逆数に対応)
SNNでBackpropするときによく使われるspikingjellyの実装を見てみるのが良い.
Spiking RFFN (Receptance Feed-Forward Networks)
- 先述のように,Spiking RFFNはTransformerのfeed-forwardブロックの代替になっている.Feed-forwardにゲーティング機構を加えたようなもの.
Z[t] = \sigma (M_P X[t]) \odot M_S(ReLU^2 (M_G X[t]))
-
Gated Linear Unit (GLU)の形になっている.
- 片方シグモイドをかけた2つの行列でアダマール積を取る形.シグモイドがかかった方の行列が,かかっていない方のどの情報を次のレイヤーに渡すかをゲーティングする.
-
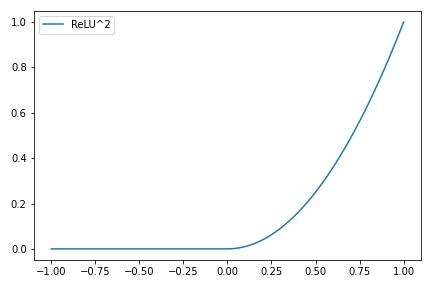
$ReLU^2$はsquared ReLUで,名の通りReLUの出力を二乗するもの.
- Transformer系のモデルではGeLUが使われることが多いと思うが,RWKVでは$ReLU^2$が使われているよう.また,$ReLU^2$の勾配は発散するので,バイナリ列で勾配が消失しやすいSNNと相性が良さそう.
結果 (preliminary)
-
Enwik8データセットを使用.
- Data compressionタスクで,bits per character(一文字表現するのに必要とする情報量)という,小さいほど良いmetricを使用する.
-
同サイズのTransformerと比べパフォーマンスは少し落ちるが,約0.045倍のSynOps(後述)を達成.
-
Transformerでは情報がfloat32で,SpikeGPTではバイナリで表現されている点も大きい.
- 前述のようにバイナリなのはspiking neuronの中でだけであることには注意.
SynOps
-
Non-zero activationのみを考慮した計算量のmetric.
- 普通のコンピュータではゼロだろうが数値であることに変わりないが,neuromorphic chipsなどevent-drivenな(スパイクが来たときだけ働く)ハードウェアで動かすとエナジー面でこの点が活きる.
動かしてみる
TO BE UPDATED




