【Java】設計未経験者に読んでほしい「千鳥格子模様」の作り方3選

はじめに

最近まともにプログラミングをしておらず、Javaの使い方や勘どころを思い出す目的で
リハビリのために簡単な模様を作ってみます。

■この記事のターゲット

• プログラミング経験はある程度経験あるけど設計は未経験

そんな方に向けた記事です。

この記事では目新しい技術はありませんが、
どのように作るか、なぜそう作るかに着目しながら模様の作り方を書いていきます。

※前置きが長いのでソースと結果だけサクッと見たい方は「準備」から読み進めてください。

■この記事を通して伝えたいこと

• 重要なのは目的に合ったやり方ができているかということ
• 設計をする場合は特に、「何をするか」ではなく「なぜそうするか」を考えてほしいということ

本記事を通して、これからシステム開発をしていく中での
設計の進め方やマインドセットの部分で少しでも参考になれば幸いです。

■「千鳥格子模様」とは？

↓↓こんな模様↓↓

千鳥格子（ちどりごうし）は、輪郭を崩したチェック模様（おおまかな方形のパターン）を持つ、二色からなる織り模様および染め模様。白黒の場合が多いが、他の色の組み合わせも用いられる。通常の千鳥格子は、平面充填の一例である。

引用元：千鳥格子(Wikipediaより)

ざっくり要約すると、

• 2色の同じ模様を隙間なく格子状に敷き詰めた模様のひとつ。
• 模様ひとつひとつが千鳥のように見えることから「千鳥格子」と呼ばれている。
• 英語では猟犬の牙に例えてhound's toothとも呼ばれる。

織り模様として作る場合はもっと複雑ですが、
今回はこの「千鳥格子模様」を単純な図形を組み合わせて3つの作り方で実装します。

序論

■構成要素を整理する

まずは「千鳥格子模様」がどんな構成で作られているか整理します。

• 2色の同じ模様を隙間なく格子状に敷き詰めた模様のひとつ。
• 模様ひとつひとつが千鳥のように見えることから「千鳥格子」と呼ばれている。

と前述した通り、

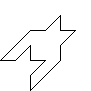
上記のような同じ形の「黒い千鳥模様」と「白い千鳥模様」で構成されていることがまず最初に分かります。

じゃあ2つの図形を順番に並べればいいじゃん！！

となりそうですが、そこは本質ではありません。

この千鳥格子模様、「黒い千鳥模様」を並べるとその隙間が「白い千鳥模様」になっています。
つまり、「黒い千鳥模様」を規則的に並べれば千鳥格子模様は作れるということ。

そのため、以降は「黒い千鳥模様」をどのように作っていくかに注目して、構成要素を整理します。

■分解してみる(その1)

まず千鳥模様にガイドラインを引いて分割します

見てわかる通り、この千鳥模様単体は以下5つの図形で構成されています。

• 正方形1つ
• 四角形2つ
• 三角形2つ

元の千鳥格子模様にもガイドラインを引いて比較すると、9分割した千鳥模様が重なりながら並べられています。

■分解してみる(その2)

例示の千鳥格子模様はわかりやすく5×5個の千鳥模様が敷き詰められています。
ただ、実際に千鳥格子模様を使っている衣服類などでは、始まりも終わりもなく敷き詰められていることも多いです。

それを考慮して枠外にも模様が並んでいる前提で考えると、以下の4つの図形の集まりにも見えます。

■実装方針

構成要素が見えたところで、今回は以下2つの方針で実装します。

• 下記をひとつの模様として考える
  

• 下記の図形の集まりとして考える
  

また、これらを「一辺に並べる個数」を指定して描画できるように実装していきます。

■準備

やることは2つ。

• まず「キャンバスのサイズ」「一辺に並べる個数」を指定するために「千鳥格子模様の設定クラス」を作成。
• 続いて千鳥格子模様を描画するためのフレームとキャンバスを作成。(※本記事のメインではないので詳細は省きます。)

ソースは以下の通りです。

Houndstooth_setup.java

// 千鳥格子模様(Houndstooth)の設定クラス
public class Houndstooth_setup {
	// 描画するキャンバスのサイズ
	private int canvasSize;
	// 一辺に並べる個数
	private int num;
	// 背景色
	private Color backgroundColor;
	// 描画色
	private Color drawColor;

	/**
	 * コンストラクタ
	 */
	public Houndstooth_setup() {
		this(600, 10, Color.WHITE, Color.BLACK);
	}

	/**
	 * コンストラクタ
	 * @param canvasSize 描画するキャンバスのサイズ
	 * @param num 一辺に並べる個数
	 * @param backgroundColor 背景色
	 * @param drawColor 描画色
	 */
	public Houndstooth_setup(int canvasSize, int num, Color backgroundColor, Color drawColor) {
		setCanvasSize(canvasSize);
		setNum(num);
		setBackgroundColor(backgroundColor);
		setDrawColor(drawColor);
	}

	public int getCanvasSize() {
		return canvasSize;
	}

	public void setCanvasSize(int canvasSize) {
		this.canvasSize = canvasSize;
	}

	public int getNum() {
		return num;
	}

	public void setNum(int num) {
		this.num = num;
	}

	public Color getBackgroundColor() {
		return backgroundColor;
	}

	public void setBackgroundColor(Color backgroundColor) {
		this.backgroundColor = backgroundColor;
	}

	public Color getDrawColor() {
		return drawColor;
	}

	public void setDrawColor(Color drawColor) {
		this.drawColor = drawColor;
	}
}

Houndstooth_main.java

public class Houndstooth_main {
	public static void main(String[] args) {
		//千鳥格子模様(Houndstooth)の設定用にインスタンス生成
		Houndstooth_setup ht = new Houndstooth_setup(300, 5, Color.WHITE, Color.BLACK); 
		
		//図形描画用のフレームを生成
		MyFrame frame = new MyFrame("千鳥格子",ht.getCanvasSize(), ht.getCanvasSize());

		//フレームに千鳥格子模様を描画したキャンバスを表示
		frame.add(new DrawCanvas(ht));
		frame.setVisible(true);
	}
}

//図形を描画するためのフレーム
class MyFrame extends JFrame{
	public MyFrame(String title, int width, int height) {
		super(title);
		setDefaultCloseOperation(EXIT_ON_CLOSE);
		getContentPane().setPreferredSize(new Dimension(width, height));
        pack();
		setLocationRelativeTo(null);
		setResizable(false);
	}
}

//千鳥格子模様を描画するためのキャンバス
class DrawCanvas extends Canvas{
	Houndstooth_setup ht;

	public DrawCanvas(Houndstooth_setup ht) {
		setSize(ht.getCanvasSize(),ht.getCanvasSize());
		setBackground(ht.getBackgroundColor());
		setHoundstooth_setup(ht);
	}

	public Houndstooth_setup getHoundstooth() {
		return ht;
	}
	
	public void setHoundstooth_setup(Houndstooth_setup ht) {
		this.ht = ht;
	}

	// 図形描画用のpaintメソッド
	public void paint(Graphics g) {
		g.setColor(ht.getDrawColor());
		// 四角形描画
		g.fillRect(10,10,100,100);
	}
}

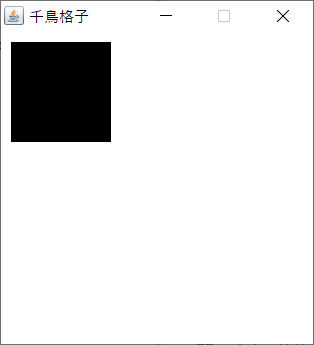
■実行結果

これで準備は完了。
以降はpaintメソッドをオーバライドして模様を作っていきます。

本論

■作り方①：ひとつの模様として考える

■概要

下記の「千鳥模様」を規則的に並べて千鳥格子模様を作成します。

ソースは以下の通りです。

Houndstooth_main.java

	// 図形描画用のpaintメソッド
	public void paint(Graphics g) {
		int length = ht.getCanvasSize() / (ht.getNum() * 2 + 1);
		int x = length;
		int y = length;
		
		for(int i = 0; i < ht.getNum(); i++) {
			for(int j = 0; j < ht.getNum(); j++) {	
				ht.drawHoundstooth2(x * j * 2, y * i * 2, length, g);
			}
		}
	}

Houndstooth_setup.java

	/**
	 * 千鳥格子模様の描画メソッド①
	 * @param x 描画の開始位置(x座標)
	 * @param y 描画の開始位置(y座標)
	 * @param length 9分割した各パーツの一辺の長さ
	 * @param g 描画用のGraphicsオブジェクト
	 */
	public void drawHoundstooth1(int x, int y, int length, Graphics g) {
		g.setColor(drawColor);
		//9分割①の描画：描画なし

		//9分割②の描画
		g.fillPolygon(
				new int[]{x + length + length / 2, x + length * 2, x + length * 2},
				new int[]{y + length, y + length, y + length / 2},
				3);
		//9分割③の描画：描画なし

		//9分割④の描画
		g.fillPolygon(
				new int[]{x + length, x + length, x + length / 2, x},
				new int[]{y + length, y + length + length / 2, y + length * 2, y + length * 2},
				4);
		//9分割⑤の描画
		g.fillRect(x + length, y + length, length, length);
		
		//9分割⑥の描画
		g.fillPolygon(
				new int[]{x + length * 2, x + length * 2, x + length * 2 + length / 2},
				new int[]{y + length, y + length + length / 2, y + length},
				3);
		//9分割⑦の描画：描画なし
		
		//9分割⑧の描画
		g.fillPolygon(
				new int[]{x + length * 2, x + length + length / 2, x + length, x + length},
				new int[]{y + length * 2, y + length * 2, y + length * 2 + length / 2, y + length * 3},
				4);

		//9分割⑨の描画：描画なし
	}

■実行結果

■説明

分かりやすいように色を変えて並べると以下の通り。

分割したパーツに番号をつけてみると

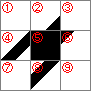
横軸では3列目(③、⑥、⑨)のパーツと、隣の模様の1列目(①、④、⑦)が重なります。
同様に縦軸では3行目(⑦、⑧、⑨)のパーツと下の模様の1行目(①、②、③)が重なります。

模様の重なりを考慮して「キャンバスのサイズ」「一辺に並べる個数」から「各パーツの一辺の長さ」を求めると

「各パーツの一辺の長さ」 = 「キャンバスのサイズ」 / ( 「一辺に並べる個数」 × 2 + 1 )

これを下記2つに使用しています。

• 千鳥模様描画の開始位置
• 千鳥模様構成している5つの図形の描画

■メリット：

• 最大のメリットは千鳥模様を基準に考えられる点

• 模様ひとつひとつが千鳥のように見えることから「千鳥格子」と呼ばれている。

と前述した通り「千鳥格子模様」から直感的に作り方がイメージできます。

最近では模様ごとに色を変えたお洒落なデザインも見かけるので、そういった場面でも有効な作り方だと言えます。

■デメリット：

• 模様の重なりを考慮する必要がある

そこまで難しい処理でもないですが、プログラミング経験が浅いと詰まるところかもしれません。

■作り方②：図形の集まりとして考える(1つ目)

■概要

下記の図形の集まりを並べて千鳥格子模様を作成します。

ソースは以下の通りです。

Houndstooth_main.java

	// 図形描画用のpaintメソッド
	public void paint(Graphics g) {
		int length = ht.getCanvasSize() / (ht.getNum() * 2);
		int x = length;
		int y = length;
		
		for(int i = 0; i < ht.getNum(); i++) {
			for(int j = 0; j < ht.getNum(); j++) {	
				ht.drawHoundstooth2(x * j * 2, y * i * 2, length, g);
			}
		}
	}

Houndstooth_setup.java

	/**
	 * 千鳥格子模様の描画メソッド②
	 * @param x 描画の開始位置(x座標)
	 * @param y 描画の開始位置(y座標)
	 * @param length 4分割した各パーツの一辺の長さ
	 * @param g 描画用のGraphicsオブジェクト
	 */
	public void drawHoundstooth2(int x, int y, int length, Graphics g) {
		g.setColor(drawColor);
		//4分割①の描画：描画なし

		//4分割②の描画
		g.fillPolygon(
				new int[]{x + length * 2, x + length + length / 2, x + length, x + length},
				new int[]{y, y, y + length / 2, y + length},
				4);
		g.fillPolygon(
				new int[]{x + length + length / 2, x + length * 2, x + length * 2},
				new int[]{y + length, y + length, y + length / 2},
				3);
		//4分割③の描画
		g.fillPolygon(
				new int[]{x + length, x + length, x + length / 2, x},
				new int[]{y + length, y + length + length / 2, y + length * 2, y + length * 2},
				4);
		g.fillPolygon(
				new int[]{x, x, x + length / 2},
				new int[]{y + length, y + length + length / 2, y + length},
				3);
		//4分割④の描画
		g.fillRect(x + length, y + length, length, length);
	}

■実行結果

■説明

分かりやすいように色を変えて並べると以下の通り。

分割したパーツに番号をつけてみると

横軸、縦軸とも「作り方①」のような重なりはありません。

そのため「キャンバスのサイズ」「一辺に並べる個数」から「各パーツの一辺の長さ」を求めると

「各パーツの一辺の長さ」 = 「キャンバスのサイズ」/(「一辺に並べる個数」×2 )

これを下記2つに使用しています。

• 千鳥模様描画の開始位置
• 千鳥模様構成している5つの図形の描画

■メリット：

• 「作り方①」のように重なっている部分がないため、図形を直感的に並べるだけで描画できる。
• 切れ目のない模様が作れる

例えばホームページの背景画像に使いたい場合、この模様を設定して繰り返し表示すれば切れ目のない背景を作ることができます。
こういった場面では「作り方①」よりも有効な作り方だと言えます。

■デメリット：

• 「千鳥模様」を意識していないため「作り方①」でできることができない

※縞々の部分を細かくしていくと「シェパードチェック」という別の模様になるそうです。(参考: いくつ知ってる？「チェック」講座②)

■作り方③：図形の集まりとして考える(2つ目)

■概要

「作り方②」と同様に、下記の図形の集まりを並べて千鳥格子模様を作成します。

方針と実行結果は「作り方②」と同じですが、縞々部分を別の方法で実装します。

ソースは以下の通りです。

Houndstooth_main.java

	// 図形描画用のpaintメソッド
	public void paint(Graphics g) {
		int length = ht.getCanvasSize() / (ht.getNum() * 2);
		int x = length;
		int y = length;
		
		for(int i = 0; i < ht.getNum(); i++) {
			for(int j = 0; j < ht.getNum(); j++) {	
				ht.drawHoundstooth3(x * j * 2, y * i * 2, length, g);
			}
		}
	}

Houndstooth_setup.java

	/**
	 * 千鳥格子模様の描画メソッド③
	 * @param x 描画の開始位置(x座標)
	 * @param y 描画の開始位置(y座標)
	 * @param length 4分割した各パーツの一辺の長さ
	 * @param g 描画用のGraphicsオブジェクト
	 */
	public void drawHoundstooth3(int x, int y, int length, Graphics g) {
		//4分割①描画：描画なし

		//4分割②描画
		g.setColor(drawColor);
		g.fillPolygon(
				new int[]{x + length * 2, x + length, x + length},
				new int[]{y, y , y + length},
				3);

		g.setColor(backgroundColor);
		g.fillPolygon(
				new int[]{x + length + length / 2, x + length, x + length},
				new int[]{y, y , y + length / 2},
				3);

		g.setColor(backgroundColor);
		g.fillPolygon(
				new int[]{x + length, x + length * 2, x + length * 2},
				new int[]{y + length, y, y + length },
				3);

		g.setColor(drawColor);
		g.fillPolygon(
				new int[]{x + length + length / 2, x + length * 2, x + length * 2},
				new int[]{y + length, y + length , y + length / 2},
				3);

		
		//4分割③描画
		g.setColor(backgroundColor);
		g.fillPolygon(
				new int[]{x, x, x + length},
				new int[]{y + length, y + length * 2, y + length},
				3);

		g.setColor(drawColor);
		g.fillPolygon(
				new int[]{x, x, x + length / 2},
				new int[]{y + length, y + length + length / 2, y + length},
				3);

		g.setColor(drawColor);
		g.fillPolygon(
				new int[]{x, x + length, x + length},
				new int[]{y + length * 2, y + length * 2, y + length},
				3);

		g.setColor(backgroundColor);
		g.fillPolygon(
				new int[]{x + length / 2, x + length, x + length},
				new int[]{y + length * 2, y + length * 2, y + length + length / 2},
				3);

		//4分割④描画
		g.setColor(drawColor);
		g.fillRect(x + length, y + length, length, length);
	}

■実行結果

■説明

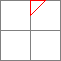
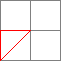
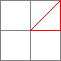
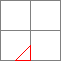
「作り方②」と異なる点は縞々部分(下記の②、③)を全て三角形で描画している点です

それぞれ以下の4つの三角形で構成しています。

縞々部分②	構成要素			縞々部分③	構成要素

fillPolygonメソッドを使用すると多角形の描画ができますが、頂点数が増えるごとに実装時の座標管理が面倒になります。
そのため「単純な図形を組み合わせて作る」という当初の方針に沿って、正方形と三角形のみで実装したのがこの作り方です。

■メリット：

「作り方②」とほぼ同じですが、付け加えるなら

• 実装時のfillPolygonメソッドの座標管理が楽になる

■デメリット：

• 「作り方②」で紹介した「シェパードチェック」への派生は、この作り方ではおススメできない

三角形をたくさん重ねればできなくはないですが、あまりスマートな作り方ではないなと思っています。

結論(まとめ)

今回の「千鳥格子模様」を作る過程は、ざっくりと以下の流れで進めました。

• 構成要素を整理する
• 実装方針を数パターン考える
• 方針に沿って実装する

ご紹介した3つの作り方についてまとめると以下の通りです。
実際には方針決めの段階で良し悪しまで考慮して、目的に合わせて使い分けをすることが重要になります。

■作り方①：ひとつの模様として考える

• メリット：
• 千鳥模様を基準に考えられる
• デメリット：
• 模様の重なりを考慮する必要がある

■作り方②：図形の集まりとして考える(1つ目)

• メリット：
• 「作り方①」のように重なっている部分がないため、図形を直感的に並べるだけで描画できる。
• 切れ目のない模様が作れる
• デメリット：
• 「千鳥模様」を意識していないため「作り方①」でできることができない

■作り方③：図形の集まりとして考える(2つ目)

• メリット：
• 実装時のfillPolygonメソッドの座標管理が楽になる
• デメリット：
• 「作り方②」で紹介した「シェパードチェック」への派生は、この作り方ではおススメできない

最後に

■この記事を通して伝えたいこと(再掲)

• 重要なのは目的に合ったやり方ができているかということ
• 設計をする場合は特に、「何をするか」ではなく「なぜそうするか」を考えてほしいということ

※「なぜそうするか」が読み取れないと、実装担当者やレビュア、後任の担当者が仕様書を見たときに
　本当に目的に合っているかの判断ができなくなります。

※また、ここでの「目的」とは「千鳥格子模様を作ること」ではなく、「千鳥格子模様を使って何がしたいのか」です。
　単純に「千鳥格子模様」を作りたいだけならどのやり方でもよいでしょう。
　ただ、本当は模様ごとに色を変えたり動きを持たせたかったのに「作り方②」で作ってしまうと、
　やりたいことが実現できず手戻りになってしまいます。

本記事を通して、これからシステム開発をしていく中での
設計の進め方やマインドセットの部分で少しでも参考になれば幸いです。