##概要:
直交検波とは、いわゆる離散フーリエ変換のことです。
ある信号に変調を加え、変調波形に対して、復調処理を施して元の波形に戻すときに使われます。
直交検波は、1つの信号に、抽出したい周波数の正弦波と、4分の1サイクルだけずらした余弦波の畳みこみを行うことで、受信信号の抽出したい周波数の振幅と位相を求めることができます
制御工学にて、ある波形を周波数領域へ変換することは、とても頻繁に使います。
直交検波を習得することで、簡単な演算で、ある波形の特性の周波数の振幅と位相を、高精度に、簡単に求めることができます。
もし、特定の周波数ではなく、全ての周波数の振幅と位相を求めたい場合は、高速フーリエ変換を使うことが望ましい方法です。
##演算アルゴリズム
直交検波は、以下の処理を行うことで実行することができます。
データ点数NNのデータxx[n]に対して,.
(1)x[n]とsin(ωt)波・cos(ωt)波の内積をとり,SS_sum,CC_sumとおく.
(2)位相はarctan(CC_sum/SS_sum)から求める。
(3)振幅は√(SS_sum^2+CC_sum^2)/N*2から求める。
##実装例
・Windows10+VisualC++2015でのExampleCodeです。
#define _USE_MATH_DEFINES
#include<iostream>
#include<vector>
#include <cmath>
using namespace std;
int main() {
vector<double> time;
vector<double> xx;
double T = 20; //周期[sec]
double phase = 0.1; //位相[rad]
double AA = 2; //振幅[%]
double NN = 200; //データ点数
double dT = 0.1; //時間刻み
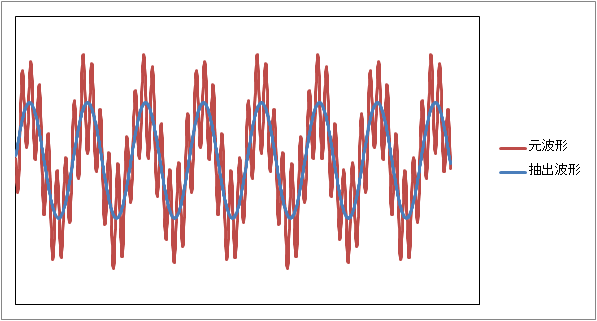
//元となる波形を生成する。
for (int n = 0; n < NN; n++) {
double data = sin(n*dT / T * 2 * M_PI + phase)*AA;
time.push_back(n*dT);
xx.push_back(data);
cout <<n*dT <<"_"<<data << endl;
}
//正弦波と余弦波を生成する
vector<double> SS;
vector<double> CC;
for (int n = 0; n < xx.size(); n++) {
double S = sin(n*dT / T * 2 * M_PI);
SS.push_back(S);
double C = cos(n*dT / T * 2 * M_PI);
CC.push_back(C);
}
//正弦波と余弦波との内積をとる。
double SS_sum = 0;
double CC_sum = 0;
for (int n = 0; n < xx.size(); n++) {
SS_sum += SS[n] * xx[n];
CC_sum += CC[n] * xx[n];
}
//振幅と位相を算出する。
double detec_phase = atan(CC_sum / SS_sum);
double detec_AA = sqrt(SS_sum*SS_sum+CC_sum*CC_sum)/NN*2;
cout <<"元信号の振幅"<<AA << "検出した振幅"<<detec_AA << endl;
cout <<"元信号の位相"<<phase <<"検出した位相"<<detec_phase << endl;
return 0;
}
###注意
直交検波・離散フーリエ変換は、以下の条件を満たさないと正しい結果を得ることができません。
・波形のサンプリング周波数が、ナイキスト周波数を満たしていること。サンプリング周波数が、抽出する周波数の2倍よりも大きいこと。
・波形のサンプリング長さが、求める周期の整数倍長であること。整数倍長でない場合は、窓関数を畳掛けすることで測定精度を改善することができます。
・波形のサンプリング長さが、求める周期の1周期よりも長いこと。
・波形に、インパルスノイズ・ステップノイズ・ホワイトノイズを含まないこと。
参考資料
インタラクティブシステム論第6回
http://kaji-lab.jp/ja/index.php?plugin=attach&refer=people%2Fkaji%2Fninshiki&openfile=ninshiki-6.pdf
NI I/Qデータとは
http://www.ni.com/white-paper/4805/ja/
位相検波回路
https://www.jspacesystems.or.jp/ersdac/Others/bookseries/errata/Errata_pdf/Vol2_170.pdf
DFT(離散フーリエ変換)
http://www.nfcorp.co.jp/techinfo/dictionary/063.html