ガウス過程回帰をnumpyで実装

ガウス過程回帰は、GPyなどの便利なライブラリもあるが、今回はnumpyで実装してみる。
データセットは前回記事を引用。

必要ライブラリのインポート

kernelRidgePredict.py

import numpy as np
np.random.seed(1)
import matplotlib.pyplot as plt
from itertools import product

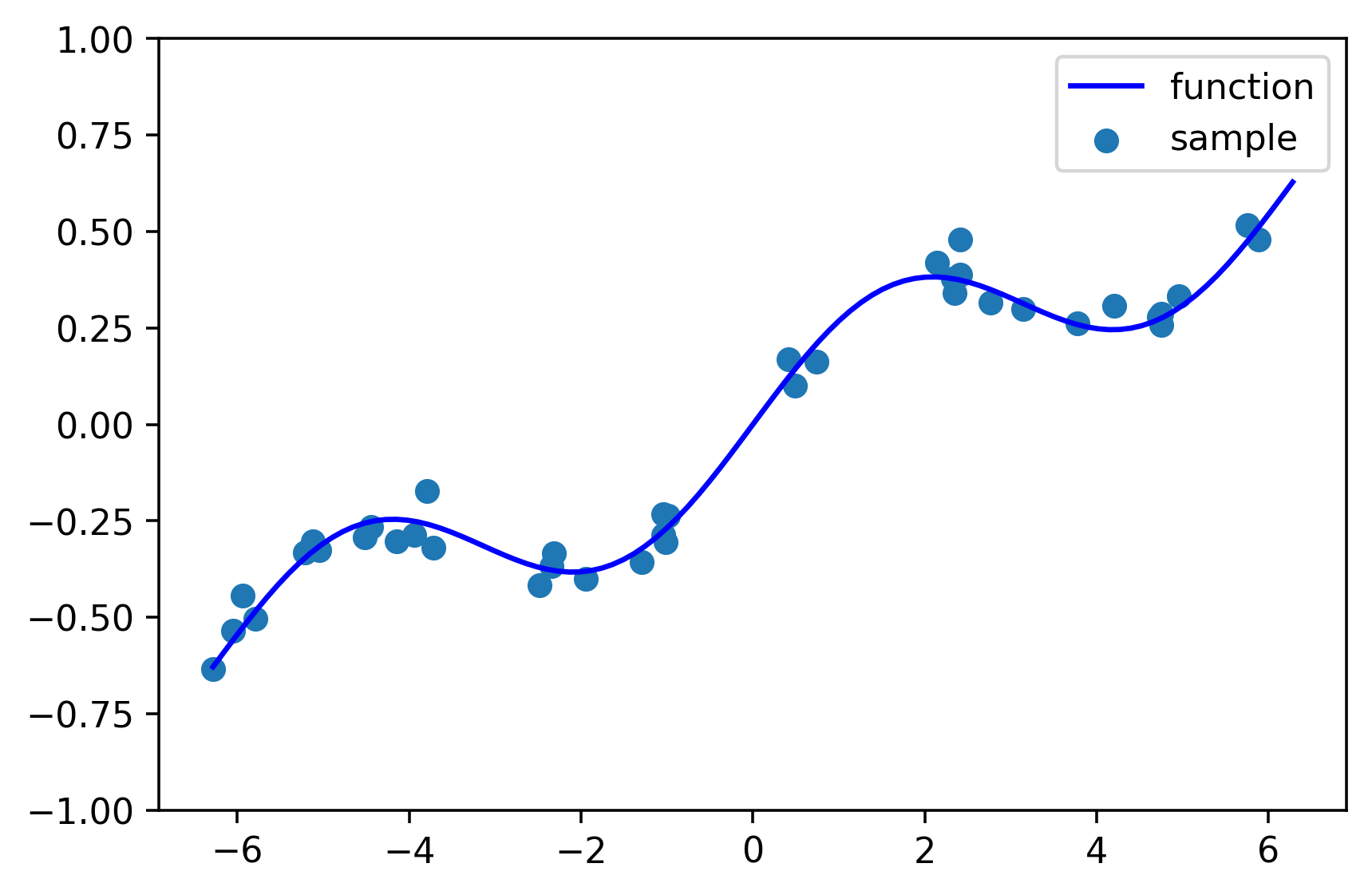
サンプルデータの生成

sin関数+1次関数に、正規分布のノイズを加える。

kernelRidgePredict.py

# 目的関数
def function(x):
    y = 0.2*np.sin(x) + 0.1*x
    return y

# データを生成
n_sample = 40
X = np.random.uniform(-2*np.pi, 2*np.pi, n_sample)
Y = function(X) + np.random.normal(loc=0, scale=0.05, size=n_sample)

# 推定したいXの値
X_pred = np.linspace(-2*np.pi, 2*np.pi, 101)

# データ数
N = n_sample

# プロット
plt.figure(figsize=(6,4), dpi=320)
plt.scatter(X, Y, label="sample")
plt.plot(X_pred, function(X_pred), c='blue', label="function")
plt.ylim(-1, 1)
plt.legend()
plt.show()

ガウス過程回帰

事前に$N$個の観測データ$\boldsymbol{x}, \boldsymbol{y}$が得られているとする。ガウス過程回帰では、予測モデル$\boldsymbol{\hat{y}}$は平均0、共分散行列$K$のガウス分布から生成されるとする。

\boldsymbol{\hat{y}} \sim N(0, K)

$K$はカーネル行列と呼ばれ、観測済みデータのすべての組み合わせでカーネル値をとったもの(データ数×データ数の行列となる)。

K=
\begin{pmatrix}
k(\boldsymbol{x}_1, \boldsymbol{x}_1)  &  k(\boldsymbol{x}_1, \boldsymbol{x}_2) & \cdots & k(\boldsymbol{x}_1, \boldsymbol{x}_N)\\
k(\boldsymbol{x}_2, \boldsymbol{x}_1)  &  k(\boldsymbol{x}_2, \boldsymbol{x}_2) & \cdots & k(\boldsymbol{x}_2, \boldsymbol{x}_N)\\
\cdots                     &  \cdots                    & \cdots & \cdots                   \\
k(\boldsymbol{x}_N, \boldsymbol{x}_1)  &  k(\boldsymbol{x}_N, \boldsymbol{x}_2) & \cdots & k(\boldsymbol{x}_N, \boldsymbol{x}_N)\\
\end{pmatrix}

カーネル関数はここでは以下のRBFカーネルを採用する。$\delta(\boldsymbol{x}, \boldsymbol{x}')$は、クロネッカーのデルタと呼ばれ、$\boldsymbol{x}$と$\boldsymbol{x}'$が等しいとき、つまりカーネル行列の対角項で1(正則化と同様の働きを持つ)、それ以外で0をとる。

k(\boldsymbol{x}, \boldsymbol{x'}) = θ_1exp\Bigl(\frac{(\boldsymbol{x} - \boldsymbol{x}')^2}{θ_2}\Bigr)+θ_3\delta(\boldsymbol{x}, \boldsymbol{x}')

ここで、新たな設計変数$\boldsymbol{x}_p$に対する予測値$y_p$を得たい場合、以下のように予測モデルを書き換える。

\begin{pmatrix}
  \boldsymbol{\hat{y}}     \\
  y_p                      \\
\end{pmatrix}

\sim N

\begin{pmatrix}
0, &

  \begin{pmatrix}
    K   & k_*        \\
    k^T_* & k_{**}     \\
  \end{pmatrix}

\end{pmatrix}

既存のデータ$D$が与えられたときの、$\boldsymbol{x}_p$に対応する$y_p$の条件付確率は以下で表すことができる。

p(y_p | \boldsymbol{x}_p, D) 

\sim N

  \begin{pmatrix}
    k^T_* K^{-1} \boldsymbol{y},  &
    k_{**}-k^T_* K^{-1} k_*
  \end{pmatrix}

gaussianProcessPredict.py

##ガウス過程回帰
# カーネル関数
def kernel(xi, xj, theta=[1, 1, 0.1]):
    delta = 1 if xi==xj else 0
    return theta[0] * np.exp(- (xi-xj)**2 / theta[1]) + theta[2]*delta

M = len(X_pred)

# カーネル行列の計算(K)
K = np.zeros((N, N))
for i, j in product(range(N), range(N)):
    K[i][j] = kernel(X[i], X[j])
    K[j][i] = K[i][j]

# カーネル行列の生成(K*)
Ks = np.zeros((N, M))
for i, j in product(range(N), range(M)):
    Ks[i][j] = kernel(X[i], X_pred[j])

# カーネル行列の生成(K**)
Kss = np.zeros((M,M))
for i, j in product(range(M),range(M)):
    Kss[i,j] = kernel(X_pred[i], X_pred[j])
    #Kss[j][i] = Kss[i][j]

# 予測
mean = Ks.T.dot(np.linalg.inv(K)).dot(Y)
covmatrix = Kss - Ks.T.dot(np.linalg.inv(K)).dot(Ks)
var = np.diag(covmatrix)

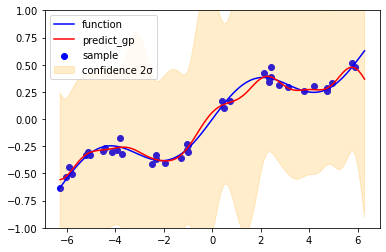
回帰結果

gaussianProcessPredict.py

# 結果を描画
plt.figure(figsize=(6,4))
plt.scatter(X, Y, label="sample", c='blue')
plt.plot(X_pred, function(X_pred), c='blue', label="function")
plt.plot(X_pred, mean, label="predict_gp", c="red")
plt.fill_between(X_pred, mean+2*np.sqrt(var) , mean-2*np.sqrt(var),
                 alpha=0.2, color="orange", label="confidence 2σ")
plt.ylim(-1, 1)
plt.legend()
plt.show()

赤いライン(予測平均)は、前回のカーネルリッジ回帰での$θ=0.1$の場合と同じになる。橙色の領域は2σ信頼区間を示しているが、幅が広くグラフの大部分を覆い隠してしまっている。これを修正するためには、ハイパーパラメータの調整が必要となる。

ガウス過程回帰(ハイパーパラメータ調整版)

オブジェクト指向に書き直し。対数尤度Lを最大化するハイパーパラメータを探索する。
最適化ソルバーには、scipy.optimize.minimize(method="SLSQP")を用いた。

gaussianProcessPredict.py

##ガウス過程回帰
class GPR:
    def __init__(self):
        print("GPR")
        self.X = None
        self.Y = None
        self.theta = [1,1,0.1]
        pass

    # データを定義
    def setData(self, X, Y):
        self.X = X
        self.Y = Y

    # ハイパラを定義
    def setHyperParameter(self, theta):
        self.theta = theta

    # カーネル関数
    def kernel(self, xi, xj):
        delta = 1 if xi==xj else 0
        return self.theta[0] * np.exp(- (xi-xj)**2 / self.theta[1]) \
                + self.theta[2]*delta

    # カーネル行列
    def kernelMatrix(self):
        # カーネル行列の計算(K)　
        N = len(self.X)
        K = np.zeros((N, N))
        for i, j in product(range(N), range(N)):
            K[i][j] = self.kernel(self.X[i], self.X[j])
            K[j][i] = K[i][j]
        return K

    # 尤度関数の定義
    def likelihood(self, theta):
        # ハイパーパラメータ
        self.theta = theta

        # カーネル行列の再計算
        K = self.kernelMatrix()

        # 尤度
        L = - np.log(np.linalg.det(K)) \
            - self.Y.T.dot(np.linalg.inv(K)).dot(self.Y)

        # デバッグ
        print(f"theta: {theta}, likelihood:{L}")

        return -1 * L  #最適化のために反転

    # ハイパーパラメータの調整
    def hyperParameterOptimizer(self):                    
        # 最小化
        opt = scipy.optimize.minimize(fun=self.likelihood, 
                                x0=[1,1,1], 
                                bounds = ((1e-6,np.inf),(1e-6,np.inf),(1e-6,np.inf)),
                                method="SLSQP")
        # 最適ハイパラを渡す
        self.theta = opt.x

    # 予測
    def predict(self, X_pred):
        # データ数
        N = len(self.X)
        M = len(X_pred)

        # 既存データからカーネル行列を生成
        K = self.kernelMatrix()

        # カーネル行列の生成(K*)
        Ks = np.zeros((N, M))
        for i, j in product(range(N), range(M)):
            Ks[i][j] = self.kernel(self.X[i], X_pred[j])

        # カーネル行列の生成(K**)
        Kss = np.zeros((M,M))
        for i, j in product(range(M),range(M)):
            Kss[i,j] = self.kernel(X_pred[i], X_pred[j])

        # 予測
        mean = Ks.T.dot(np.linalg.inv(K)).dot(Y)
        covmatrix = Kss - Ks.T.dot(np.linalg.inv(K)).dot(Ks)
        var = np.diag(covmatrix)

        return mean, var

# 推定
gp = GPR()
gp.setData(X,Y)
gp.hyperParameterOptimizer()
mean, var = gp.predict(X_pred)

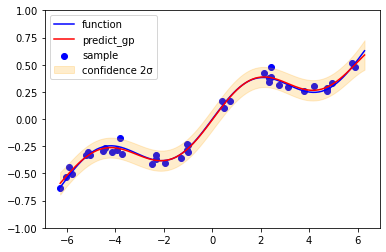
回帰結果(ハイパーパラメータ調整後)

gaussianProcessPredict.py

# 結果を描画
plt.figure(figsize=(6,4))
plt.scatter(X, Y, label="sample", c='blue')
plt.plot(X_pred, function(X_pred), c='blue', label="function")
plt.plot(X_pred, mean, label="predict_gp", c="red")
plt.fill_between(X_pred, mean+2*np.sqrt(var) , mean-2*np.sqrt(var),
                 alpha=0.2, color="orange", label="confidence 2σ")
plt.ylim(-1, 1)
plt.legend()
plt.show()

尤度最大化によって求めたハイパーパラメータは、Θ=[3.43209672e-01, 1.34840982e+01, 1.84642705e-03]。
先ほどと比べ、2σ信頼区間の幅が妥当になっている。