カーネルリッジ回帰をnumpyで実装

カーネルリッジ回帰は、sklearn.kernel_ridgeなどの便利なライブラリもあるが、今回はnumpyで実装してみる。

##必要ライブラリのインポート

kernelRidgePredict.py

import numpy as np
np.random.seed(1)
import matplotlib.pyplot as plt
from itertools import product

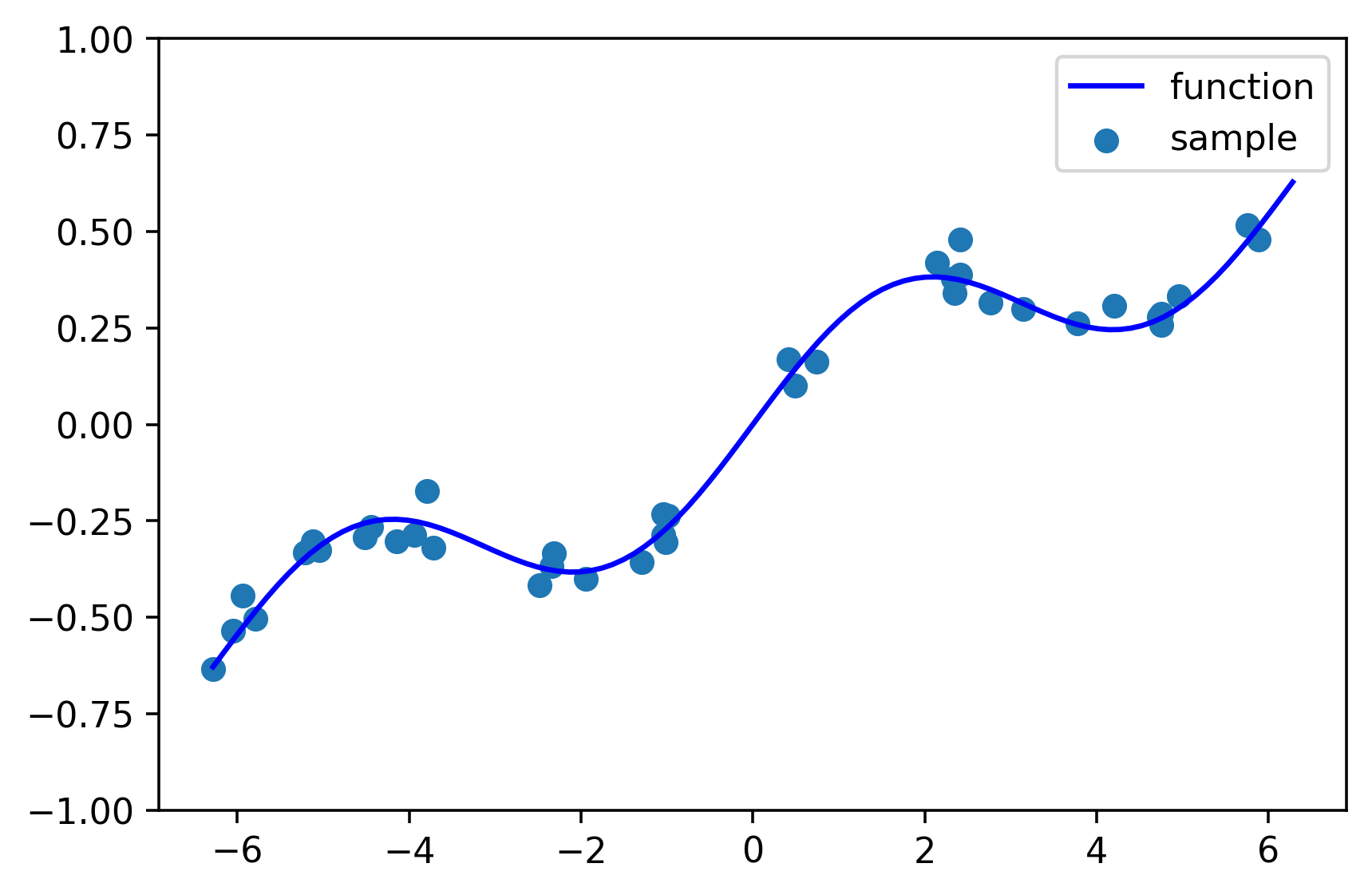
##サンプルデータの生成
sin関数+1次関数に、正規分布のノイズを加える。

kernelRidgePredict.py

# 目的関数
def function(x):
    y = 0.2*np.sin(x) + 0.1*x
    return y

# データを生成
n_sample = 40
X = np.random.uniform(-2*np.pi, 2*np.pi, n_sample)
Y = function(X) + np.random.normal(loc=0, scale=0.05, size=n_sample)

# 推定したいXの値
X_pred = np.linspace(-2*np.pi, 2*np.pi, 101)

# データ数
N = n_sample

# プロット
plt.figure(figsize=(6,4), dpi=320)
plt.scatter(X, Y, label="sample")
plt.plot(X_pred, function(X_pred), c='blue', label="function")
plt.ylim(-1, 1)
plt.legend()
plt.show()

##カーネルリッジ回帰
事前に$N$個の観測データ$\boldsymbol{x}_o, \boldsymbol{y}_o$が存在する場合、
カーネルリッジでは、以下のように予測モデルを表現する。

\hat{y} = \sum_{j=1}^{N} w_j k(\boldsymbol{x}_{o}^{(j)}, \boldsymbol{x})

$\boldsymbol{x}_{o}^{(j)} (j=1,2,3 \cdots N) $は観測済み(Observation)データの説明変数ベクトル($j$はデータのインデックスを示す)、$\boldsymbol{x}$はこれから予測したい説明変数ベクトルを示す。

つまり、予測モデルを$\hat{y}$を、重みベクトル$w_j (j=1,2,3 \cdots N)$と、カーネル関数ベクトル$k(\boldsymbol{x}_o^{(j)}, \boldsymbol{x}) (j=1,2,3 \cdots N)$との線形結合で表現している。

カーネル関数はここでは以下のRBFカーネルを採用する。
$θ$はハイパーパラメータと呼ばれ、RBFカーネルの裾の長さを制御するものであるが、ここでは$θ=1$で固定する。(二乗誤差の最小化などでパラメータを調整するとなお良い)

k(\boldsymbol{x}, \boldsymbol{x'}) = exp\Bigl(\frac{(\boldsymbol{x} - \boldsymbol{x}')^2}{θ}\Bigr)

重み係数$w$は以下のように求める。

\boldsymbol{w} = (K+αE)^{-1}\boldsymbol{y} \\

K=
\begin{pmatrix}
k(\boldsymbol{x}_o ^{(1)}, \boldsymbol{x}_o ^{(1)})  &  k(\boldsymbol{x}_o ^{(1)}, \boldsymbol{x}_o ^{(2)}) & \cdots & k(\boldsymbol{x}_o ^{(1)}, \boldsymbol{x}_o ^{(N)})\\
k(\boldsymbol{x}_o ^{(2)}, \boldsymbol{x}_o ^{(1)})  &  k(\boldsymbol{x}_o ^{(2)}, \boldsymbol{x}_o ^{(2)}) & \cdots & k(\boldsymbol{x}_o ^{(2)}, \boldsymbol{x}_o ^{(N)})\\
\cdots                     &  \cdots                    & \cdots & \cdots                   \\
k(\boldsymbol{x}_o ^{(N)}, \boldsymbol{x}_o ^{(1)})  &  k(\boldsymbol{x}_o ^{(N)}, \boldsymbol{x}_o ^{(2)}) & \cdots & k(\boldsymbol{x}_o ^{(N)}, \boldsymbol{x}_o ^{(N)})\\
\end{pmatrix}

$K$はカーネル行列と呼ばれ、観測済みデータのすべての組み合わせでカーネル値をとったもの(データ数×データ数の行列となる)。$αE$は正則化項で、カーネル行列の対角成分に微小量を入れることで、過学習を抑止する(極端な重みの偏りを防ぐ)作用がある。

kernelRidgePredict.py

##カーネルリッジ
# ハイパーパラメータ
theta = 1
alpha = 0.001

# カーネル関数を定義
def kernel(x, xd, theta):
    k = np.exp(- (x-xd)**2 / theta)
    return k

# カーネル行列の計算
K = np.zeros((N, N))
for i, j in product(range(N), range(N)):
    K[i][j] = kernel(X[i], X[j], theta)

# 重みの計算
weight = np.linalg.inv(K + alpha * np.eye(N)).dot(Y)

# カーネル回帰
def kernel_predict(X, X_pred, weight, theta):
    Y_pred = 0
    for i in range(len(X)):
        Y_pred += weight[i] * kernel(X[i], X_pred, theta)
    return Y_pred


# 回帰によって結果を予測        
Y_pred = np.zeros(len(X_pred))
for i in range(len(X_pred)):
    Y_pred[i] = kernel_predict(X, X_pred[i], weight, theta)

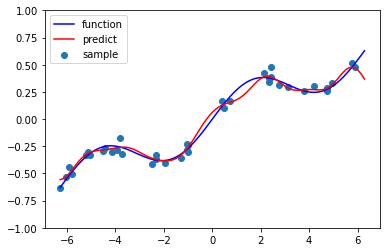
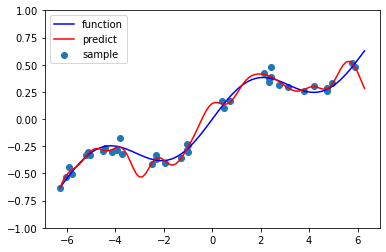
回帰結果

kernelRidgePredict.py

# 結果を描画
plt.figure(figsize=(6,4))
plt.scatter(X, Y, label="sample")
plt.plot(X_pred, function(X_pred), c='blue', label="function")
plt.plot(X_pred, Y_pred, c="red", label="predict")
plt.ylim(-1, 1)
plt.legend()
plt.show()

alpha = 0.1

alpha = 0.001

alpha = 0.00001

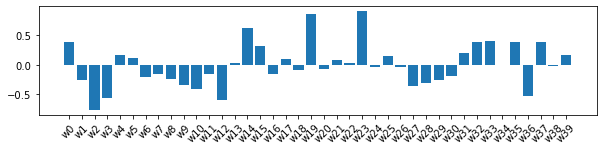
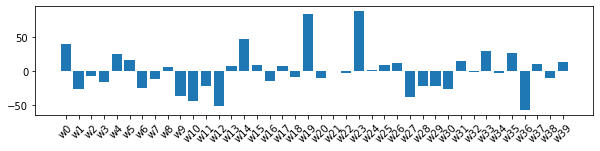
重みの分布

kernelRidgePredict.py

# 重みのプロット
leg = np.array(range(N))
plt.figure(figsize=(10,2))
plt.bar([f"w{l}" for l in leg], weight)
plt.xticks(rotation=45)

alpha = 0.1

alpha = 0.001

alpha = 0.00001

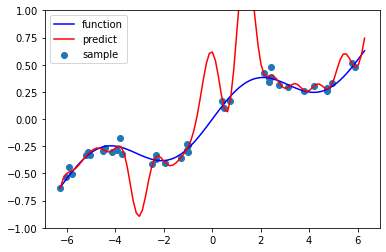
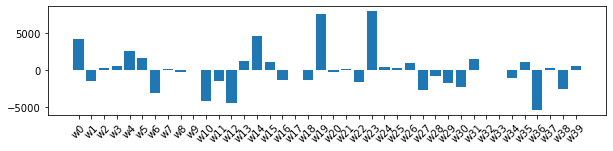
$α=0.00001$の時は、重み係数のオーダーが大きくなり、回帰も過学習ぎみになる。