サイコロを振る

#サイコロを振る。
pythonを用いて、簡単なサイコロ試行を実装してみる。

##必要なライブラリのインポート

import numpy as np
import matplotlib.pyplot as plt

##サイコロを振る
サイコロをN回振って、出目のヒストグラムを作成する。
N=100だとばらつきがあるが、N=10000だとすべての目の出現率がほぼ同等になる。

# 出目を用意
dice = [1,2,3,4,5,6]

# サイコロを投げる関数
def throwDice(N):
    result = np.random.choice(dice, N, replace=True)
    return result

# 出目のヒストグラム
plt.figure()
for n in [100,10000]:
    plt.hist(throwDice(n), bins=6, density=True, alpha=0.3, label="N={}".format(n))
plt.legend()

###出目の確率を調整したサイコロを振る
イカサマサイコロを振る。
1,2,3の目に対して4,5の目は3倍出現しやすく、6の目は6倍出現しやすい。

# 確率分布を変更
pb = np.array([1,1,1,3,3,6]); pb = pb/np.sum(pb)

# 確率分布を調整したサイコロを投げる関数
def throwDicePb(N):
    result = np.random.choice(dice, N, p=pb, replace=True)
    return result

# ヒストグラム
plt.figure()
for n in [100,10000]:
    plt.hist(throwDicePb(n), bins=6, density=True, alpha=0.3, label="N={}".format(n))
plt.legend()

##サイコロをN投げてその平均をとる

#　サイコロをN回投げて平均をとる
def throwDiceMean(size, N):
    result = [np.mean(throwDice(N)) for i in range(size)]
    return result

# サイコロを10回投げて平均をとる試行をs回行う
plt.figure() 
for s in [100,10000]:
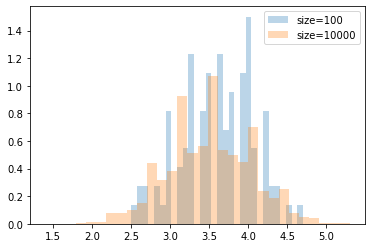
    plt.hist(throwDiceMean(s,10), bins=30, density=True, alpha=0.3, label="size={}".format(s))
plt.legend()

サイコロの目の平均値3.5を中心とした正規分布に近づく。

##同様の試行をイカサマサイコロで行う

def throwDiceMeanPb(size, N):
    result = [np.mean(throwDicePb(N)) for i in range(size)]
    return result

# サイコロを10回投げて平均をとる試行をs回行う
plt.figure() 
for s in [100,10000]:
    plt.hist(throwDiceMeanPb(s,10), bins=30, density=True, alpha=0.3, label="size={}".format(s))
plt.legend()

こちらも試行回数を増やしていくほど、正規分布に近付く。