はじめに
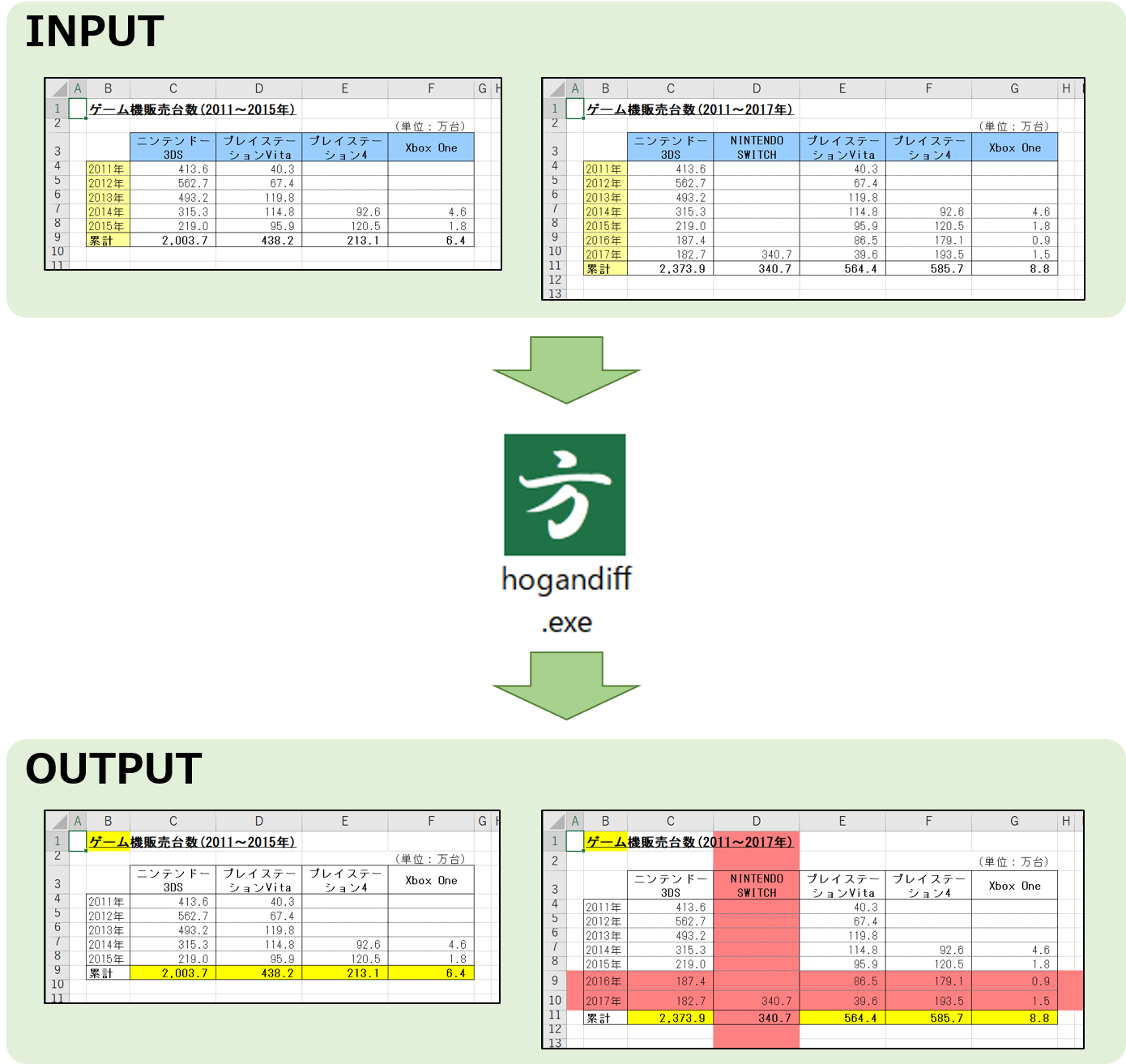
以前の投稿で、Excel比較ツール「方眼Diff」を公開しました。行や列の差分を自動で検出してくれる優れものです。
挿入された行・列が赤色に、変更されたセルが黄色に着色されて表示されます。処理速度も十分に実用的です。騙されたと思って一度使ってやってみてくださいな。→ 方眼Diffのサイト
今回はこれを題材として、Excelシート同士の2次元diffを求めるアルゴリズムを紹介します。
文字列のdiff
さて、まずは文字列同士のdiffから始めましょう。次の2つの文字列を比べることを考えます。
BEAUTIFUL SUN vs DUTIFUL SON
この2つの文字列に含まれる文字同士の最も妥当な対応関係を求めることがゴールとなります。
これくらい短い文字列であれば直感的に答えを得ることができますね。
文字列1: B E A U T I F U L _ S U N
| | | | | | | | |
文字列2: D U T I F U L _ S O N
では、これをプログラムで自動的に求めるためにはどうしたらよいでしょうか?
経路最適化問題に置き換える
「文字列同士のdiffを求める」という命題はややざっくりしていますので、より明確な形に定義しなおす必要があります。
次の2つのステップにより経路最適化問題に置き換えることが一般的であり、プログラムで自動化するうえで有効です。
①文字の対応関係をグラフ上の経路で表す
比較対象の文字列をタテ・ヨコに並べて二次元格子状のグラフを作成します。そして2つの文字列に含まれる文字の対応関係を、グラフの左上の始点から右下の終点への経路で表すのです。
赤線で示した経路は、上で示した対応関係を表します。

グラフを下に進むことは、文字列1に含まれる文字が余剰であることを表します。グラフを右に進むことは、文字列2に含まれる文字が余剰であることを表します。そしてグラフを右下に進むことは、文字列1に含まれる文字と文字列2に含まれる文字が対応することを表します。
従ってグラフを右下に進むことができるのは、行先のタテ・ヨコの文字が同じである場合だけです。
このグラフはエディットグラフと呼ばれます。
②グラフ上の経路に通過コストを設定する
文字の対応関係をグラフ上の経路で表すことができたら、次はその経路に "通過コスト" を設定します。
いま私たちは文字列1と文字列2に含まれる文字のより多くが一致するような対応関係を求めたい、言い換えれば余剰となるような文字がより少なくなるような対応関係を求めたいわけですから、文字の余剰に相当する経路には大きなコストを、文字の一致に相当する経路にはより小さなコストを設定すべきです。
この考え方に基づき、グラフを下または右に進む場合はコスト1、右下に進む場合はコスト0を設定することにしましょう。
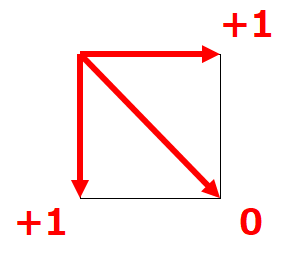
以上により、「2つの文字列に含まれる文字同士の最適な対応関係を求める」という問題を、「エディットグラフ上の始点から終点へのコストが最小となるような経路を求める」という経路最適化問題に定義しなおすことができました。
あとはこれを解けばよいだけです。
経路最適化問題を解く
さて、エディットグラフ上の始点から終点へのコスト最小経路を求めるにはどうしたらよいでしょうか?
文字列1の長さが$M$、文字列2の長さが$N$のとき、始点から終点への順方向の経路の数はナナメ方向の経路を無視すると $_{M+N}C_M$ 通りとなります。これを全部列挙してそれぞれのコストを求めることもできますが、あまりスマートなやり方ではありませんね。
これは動的計画法を利用して計算することができます。
グラフ上のある点に到達するために必要なコストの最小値は、そのひとつ上流の点への最小到達コストを $a, b, c$ とすると、$min(a, b+1, c+1)$ という漸化式で表すことができます。
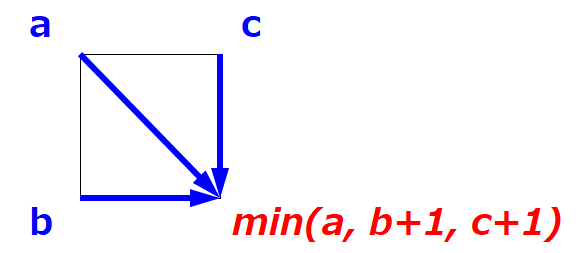
これをグラフの始点に近い点から順に適用していくことで、終点を含む全ての点の最小到達コストを求めることができます。

ここまで来れば後は簡単ですね。グラフ終点から最小コストの経路を遡ることで、始点から終点へのコスト最小経路を求めることができます。
(最小コストの経路が複数ある場合は、縦経路と横経路のどちらを優先させるかの決めの問題です。)
以上が文字列のdiffを求めるオーソドックスな方法です。
本稿ではイメージを優先させましたが、ググればより詳細かつ厳密な解説をたくさん見つけることができます。
Excelのdiffへの応用
これまで見てきた通り、文字列、つまり文字を要素とするリスト同士のdiffは、エディットグラフと動的計画法を用いて求めることができました。
「方眼Diff」ではこの考え方をExcelシート同士のdiffに応用しています。
すなわち、
- 行を要素とするリスト同士の比較により、2つのExcelシートの行同士の対応関係を求める
- 列を要素とするリスト同士の比較により、2つのExcelシートの列同士の対応関係を求める
- 行・列それぞれの対応関係に基づいてセル同士の対応関係を求め、それらの内容を比較する
という方法を採用しています。
エディットグラフ上の通過コスト(以降は編集コストと呼ぶことにしましょう)についてもアレンジを加えています。
文字列同士のdiffにおいては次表のようにしていました。
| エディットグラフ上の経路 | 意味合い | 編集コスト |
|---|---|---|
| グラフを下に進むこと | 文字列1に含まれる文字が余剰である | +1 |
| グラフを右に進むこと | 文字列2に含まれる文字が余剰である | +1 |
| グラフを右下に進むこと | 文字列1に含まれる文字と文字列2に含まれる文字が対応する | 0 |
これに対して、「方眼Diff」では次の方法を採用しています。
| エディットグラフ上の経路 | 意味合い | 編集コスト |
|---|---|---|
| グラフを下に進むこと | シート1に含まれる行または列が余剰である | その行または列に含まれる空でないセルの数 |
| グラフを右に進むこと | シート2に含まれる行または列が余剰である | その行または列に含まれる空でないセルの数 |
| グラフを右下に進むこと | シート1に含まれる行または列とシート2に含まれる行または列が対応する | それらの行または列に含まれる空でないセルのうち、内容が一致しないものの数 |
正直なところ、上表に記載した編集コストは「とりあえず」で設計したものなのですが、出来上がったプログラムを色々と動かすなかで、十分に実用的であることが分かりました。
編集コストの計算方法は、精度と処理時間のトレードオフで様々な方式が考えられますから、この部分をストラテジーパターンとしておきユーザーが選べるようにすると、ツールとしてより便利になるかもしれませんね。(時間ができたら実装したいと思います。)
※2024.4.11追記
上表の編集コストでは場合により人間の直観とは異なる評価結果が得られることが分かったため、方眼Diff v0.18.0 で行ごと/列ごとの重みづけを加味した評価関数(編集コスト)を導入しました。
改善の余地
ここまで紹介したように、「方眼Diff」は文字列同士のdiffのアルゴリズムをベースとして、必要な点をアレンジしたものでした。
現時点でも十分実用的なのですが、改善の余地がないわけではありません。これについて最後に記します。
計算量の削減
「方眼Diff」では、エディットグラフ上のすべての点について最小到達コストを計算しています。従って行同士の対応関係を求めるとき、比較対象シートの行数を$R$、列数を$C$とすると、計算すべき点の数は $R^2$ となります。さらに、本稿では詳しくふれませんでしたが、ある点の編集コストの計算量は $O(C)$ となります。従って行の挿入/削除を考慮して2つのシートを比較するときの最終的な計算量は $O(CR^2)$ となり、加えて列の挿入/削除も考慮する場合は $O(CR^2 + C^2R)$ となります。
一方、文字列同士のdiffでは、編集コストが $+1$ か $0$ のいずれかであることを利用して、計算範囲をエディットグラフの対角線付近の一部に限定して処理を大幅に効率化するアルゴリズムが知られています。
「方眼Diff」についても、編集コストの算出方法を工夫することにより探索範囲を限定し、処理を効率化することができるかもしれません。
異なるアルゴリズムの可能性
「方眼Diff」は行方向・列方向それぞれについて2つのシートの対応関係を計算し、それらを統合して最終的な結果を得るという方法を採用しています。
一方、全く異なるアルゴリズムでシート同士のdiffを求めることも可能かもしれません。
たとえば、
- 2つのシートから似た内容のセルを見つけだす
- それらの移動ベクトルを調べる
- 移動ベクトルに、セル内容の複雑さ/類似度/シート内におけるユニークさに応じて重みづけをする
- 重みの合計が最大となるような行・列の対応関係を求める
というようなアルゴリズムも可能かもしれません。
このアルゴリズムの場合は行/列の対応関係を一気に求めるため、もしかすると行/列の対応関係をそれぞれ求める現在の方式よりも高い精度が得られるかもしれません。
暇なときに実装にチャレンジしたいと思います。
おわりに
以上、今回は 以前の投稿 で紹介したExcel比較ツール「方眼Diff」で採用しているdiff計算アルゴリズムについて紹介しました。
私自身は計算機科学の専門的な教育を受けたことがないので、アルゴリズムだとかその実装だとかは正直苦手です。ただ、それを身につけ工夫することで実現できることの幅が広がることを、今回あらためて実感した次第です。
アルゴリズムの勉強をしようとしたとき、大学の研究室のWebサイトがよくヒットします。これらは説明の厳密さを重視するあまり数式マシマシになり、初心者にはハードル高めに感じられるものです。
Qiitaはその一段手前の、入門者にやさしいコミュニティであってほしいと個人的には思っています。(もちろん、専門性の高い投稿も大変興味深く有益で、有難いものです。)
日本のプログラマーコミュニティの底上げのために、益々の発展を願っています。私自身も微力ながら貢献できればと思いつつ、自らの趣味欲を満たしている次第です。