はじめに
協調フィルタリングでは行列分解が広く用いられている．協調フィルタリングにおける行列分解については，以下の記事を参考にしていただきたい．
この記事では，よく使われるの行列分解基準を，重み付き最小二乗法として定式化することで効率的に解を計算する手法について考察する．
基本的な行列分解
さて，協調フィルタリングで使われる行列分解は基本的に以下の最適化問題を解くことにより達成される．しかし，この問題は解析的に解を求めることができないため，通常は確率的勾配法を用いて解を求める．
\min_{\boldsymbol{X},\boldsymbol{Y}} \ \sum_{(i,j):r_{ij}\neq0} \left(r_{ij}-\boldsymbol{x}_i^T\boldsymbol{ y}_j\right)^2+\alpha\left(\sum_{i=1}^m \|\boldsymbol{x}_i\|^2+\sum_{j=1}^n \|\boldsymbol{y}_j\|^2\right)
重み付き最小二乗法による行列分解
ここで，文献をさらっと一つ紹介する．
- Collaborative Filtering for Implicit Feedback Datasets [Hu et al. ICDM2008]
この論文では，重み付き行列分解 (Weighted Matrix Factorization) により，Implicit Feedbackを扱う手法を提案している．しかし，この記事では，もっと話を単純にするためにExplicit Feedbackつまりレーティングを扱う際に，このアイデアを使ってみる．
このアイデアを元に，上記の最適化問題は重み付き最小二乗法として以下のように書き下すことができる．
\min_{\boldsymbol{X},\boldsymbol{Y}} \ \sum_{i=1}^m \sum_{j=1}^n c_{ij} \left(r_{ij}-\boldsymbol{x}_i^T\boldsymbol{ y}_j\right)^2+\alpha\left(\sum_{i=1}^m \|\boldsymbol{x}_i\|^2+\sum_{j=1}^n \|\boldsymbol{y}_j\|^2\right)
ここで，
c_{ij}=\left\{
\begin{array}{ll}
1 & (r_{ij} > 0) \\
0 & (r_{ij} = 0) \\
\end{array}
\right.
である．レーティングされていないペアに対しては重みが０なので，学習に影響はない．そうすると，この各$\boldsymbol{x}_i,\boldsymbol{y}_j$は以下のように解析的に求めることができる．
\hat{\boldsymbol{x}}_i=\left(\boldsymbol{Y}^T\boldsymbol{C}_i\boldsymbol{Y}+\alpha\boldsymbol{I}_k\right)^{-1}\boldsymbol{Y}^T\boldsymbol{C}_i\boldsymbol{r}_i \\
\hat{\boldsymbol{y}}_j=\left(\boldsymbol{X}^T\boldsymbol{C}_j\boldsymbol{X}+\alpha\boldsymbol{I}_k\right)^{-1}\boldsymbol{X}^T\boldsymbol{C}_j\boldsymbol{r}_j
ここで，
\begin{align}
\boldsymbol{C}_i &= diag(c_{i1},\ldots,c_{in}), \ \boldsymbol{C}_j = diag(c_{1j},\ldots,c_{mj}) \\
\boldsymbol{r}_i &= [r_{i1}|\cdots|r_{in}]^T , \ \boldsymbol{r}_j = [r_{1j}|\cdots|r_{mj}]^T
\end{align}
である．よって，適当な$Y$から，上記の更新式で解を求めていくことができる．これは，２変数関数を最適化する際に片方の変数を固定して片方を最適化する，というものと同じだ．今回の場合，片方の変数を固定すると，もう片方が瞬時に決まるので（逆行列計算が必要だが），収束が早くなると考えらえる．
実験
計算時間がどれだけ変わるかを人口データを用いて実験する．この際に，性能が落ちては意味がないので，性能も合わせて比較する．また，単純な興味から，サンプル数を変えてどれだけ性能が変わるかも考察する．
データは以下の要領で生成する．
1. 隠れベクトルの次元$k$, ユーザ数$m$, アイテム数$n$を適当に決める．ここでは$k=2, m=10, n=10$とする．
2. $\boldsymbol{X}\in \mathbb{R}^{m\times k},\boldsymbol{Y} \in \mathbb{R}^{n\times k}$を適当に生成
3. レーティング行列，$R=min(max(\boldsymbol{X}\boldsymbol{Y}^T,1),5)$，を生成．$r_{ij} \in {1,2,3,4,5}$に修正．
4. スパース率$s$に従って，$\boldsymbol{R}$の幾つかの要素をゼロにする．
ゼロ要素をどれだけ正しく復元できるかをRMSEで測る．だいたい0.5以下に抑えることができれば良い性能だと言えると思う．なお，隠れベクトルの次元$k$は既知だとする．通常の行列分解の実装は以下のコードを使わせていただいた．
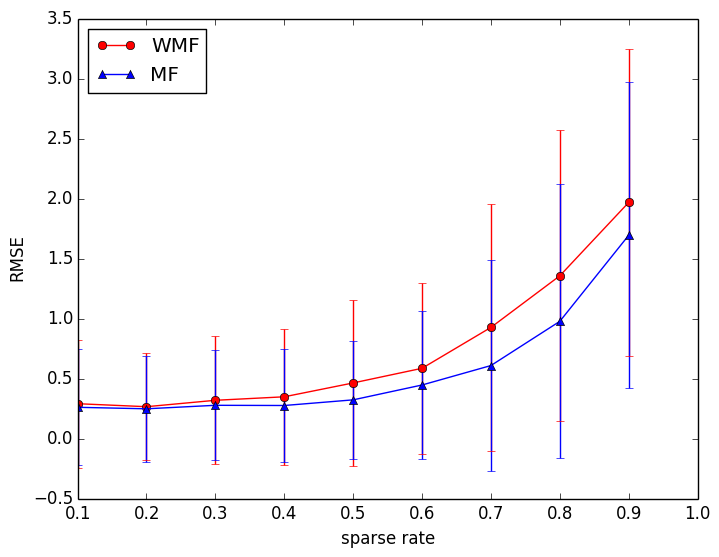
実験はsparse rateを変えながら行い，各sparase rateにおいて20回試行しその平均，標準偏差をプロットする．
図1にsparse rateを変えたときのRMSEを示す．sparse rateが高いほどトレーニングサンプルが少なくなるので，性能は落ちる．トレーニングサンプルが多いときは，WMF，MFともに性能変わらない．サンプルが減っていくにつれて，ともに性能は落ちていくが，サンプルが非常に少ないところではMFの方が少し性能が良い．確率的勾配法はサンプル数が少ないときでも性能があまり落ちないのでしょうか？
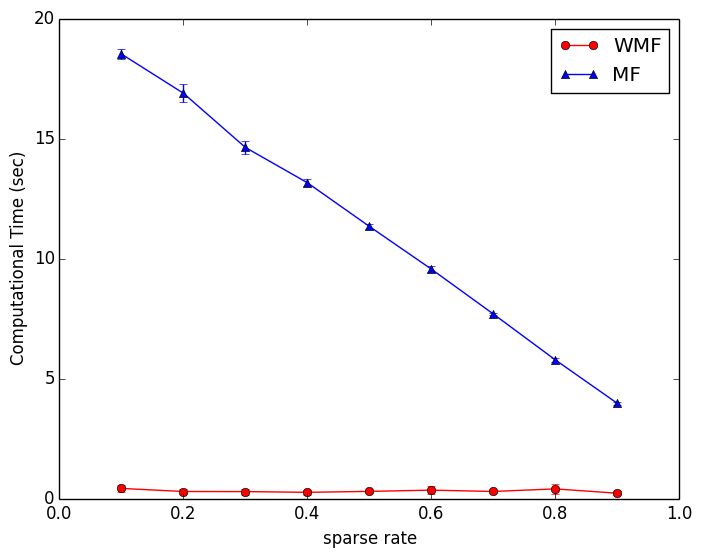
図2にsparse rateを変えたときの計算時間を示す．通常のMFでは，sparse rateが高いほどトレーニングサンプルが少なくなるので，計算時間は減っていく．一方，WMFではトレーニングサンプルに関わらず計算時間は一定である．このグラフから，計算時間が大幅に短縮されていることがわかる．
図1: sparse rateを変えたときのRMSE
図2: sparse rateを変えたときの計算時間
まとめ
重み付き最小二乗法により，計算時間を大幅に削減することができた．しかしながら，トレーニングサンプルが少ないときに，MFより性能が少し劣るのが気がかり．半分くらい埋まっているレーティング行列に対してはこのアプローチは有効かもしれない．とりえあずこの理由を解明したい．というより何か理由がわかったら教えてください．
WMF.py: https://gist.github.com/nkt1546789/05cdecbc0a7533ef3027
戯言
qiitaでテキストを中央揃えするやり方がわかりませんでした．どなたか教えてください 