はじめに
CVPR2018にて採択された "ST-GAN: Spatial Transformer Generative Adversarial Networks for Image Compositing" について読みましたので、まとめていこうと思います。
本記事では実装ではなく論文自体を理解することを目的に説明していきます。なので英語論文をさくさく読める方はそちらを読んだほうが良いかと思われます。
基本的に論文の構成のまま、関連研究など本筋に無関係なもの以外についてはあまり省略せずに説明していきます。
Tips
- Title
- ST-GAN: Spatial Transformer Generative Adversarial Networks for Image Compositing [論文リンク]
- Conference
- CVPR (Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition) 2018
- Authors
- Chen-Hsuan Lin$^{1*}$, Ersin Yumer$^{2,3}$, Oliver Wang$^2$, Eli Shechtman$^2$, Simon Lucey$^{1,3}$
$^1$Carnegie Mellon University, $^2$Adobe Research, $^3$Argo AI
$^*$Work done during CHL’s internship at Adobe Research.
0. Abstract
本研究では、背景画像に前景オブジェクトを配置するような問題について考えます(例: 室内の画像に家具画像を配置する問題、顔画像にサングラスを配置する問題)。
この問題に対処する方法として、筆者らは、Spatial Transformer Networks (STNs) [解説記事] をGeneratorに用いたGANs、Spatial Transformer GANs (ST-GANs) を提案します。
※STNs ... CNNに画像を入力する前に画像を自動で幾何学的に変換(移動・縮小・回転・切り取りなど)することで画像の歪みを修正し、予測に必要な部分のみをネットワークに流すようなアーキテクチャ。変換因子の推定を誤差逆伝搬により学習させることができる。
ST-GANは、背景画像と前景オブジェクトを入力にとり、前景オブジェクトの変換因子を出力とすることで、その変換により画像合成を行えるようなアーキテクチャとなります。
ST-GANでは画像を直接推定するのではなく画像の変換因子を推定するので、間接的に高解像度の画像へ適用することが可能となります。
1. Introduction
Convolutional Neural Networks (CNNs) の出現により画像生成の分野は大きく進歩しましたが、その中でもとりわけGenerative Adversarial Networks (GANs)は現実的な画像生成においてとりわけ強力なツールとなっています。
GANsでは、ベクトルから画像を生成する Generator Network ($G$) と、画像が現実のものか G によって生成された偽物か識別する Discriminator Network ($D$) の二種のネットワークが用意され、相互に学習しあうminimaxゲームが行われます。
しかしベクトルから画像を生成する際に、表現可能な空間がネットワークの容量によって制限されるので、これは限られた領域(顔の画像を生成するなど)での画像生成でのみうまく機能します。
そこで筆者らは、ST-GANs というフレームワークを提案します。これは、背景画像に前景オブジェクトを配置するような問題に対して、幾何学的変換の変換因子をGANのフレームワークの中で学習するようなフレームワークです。
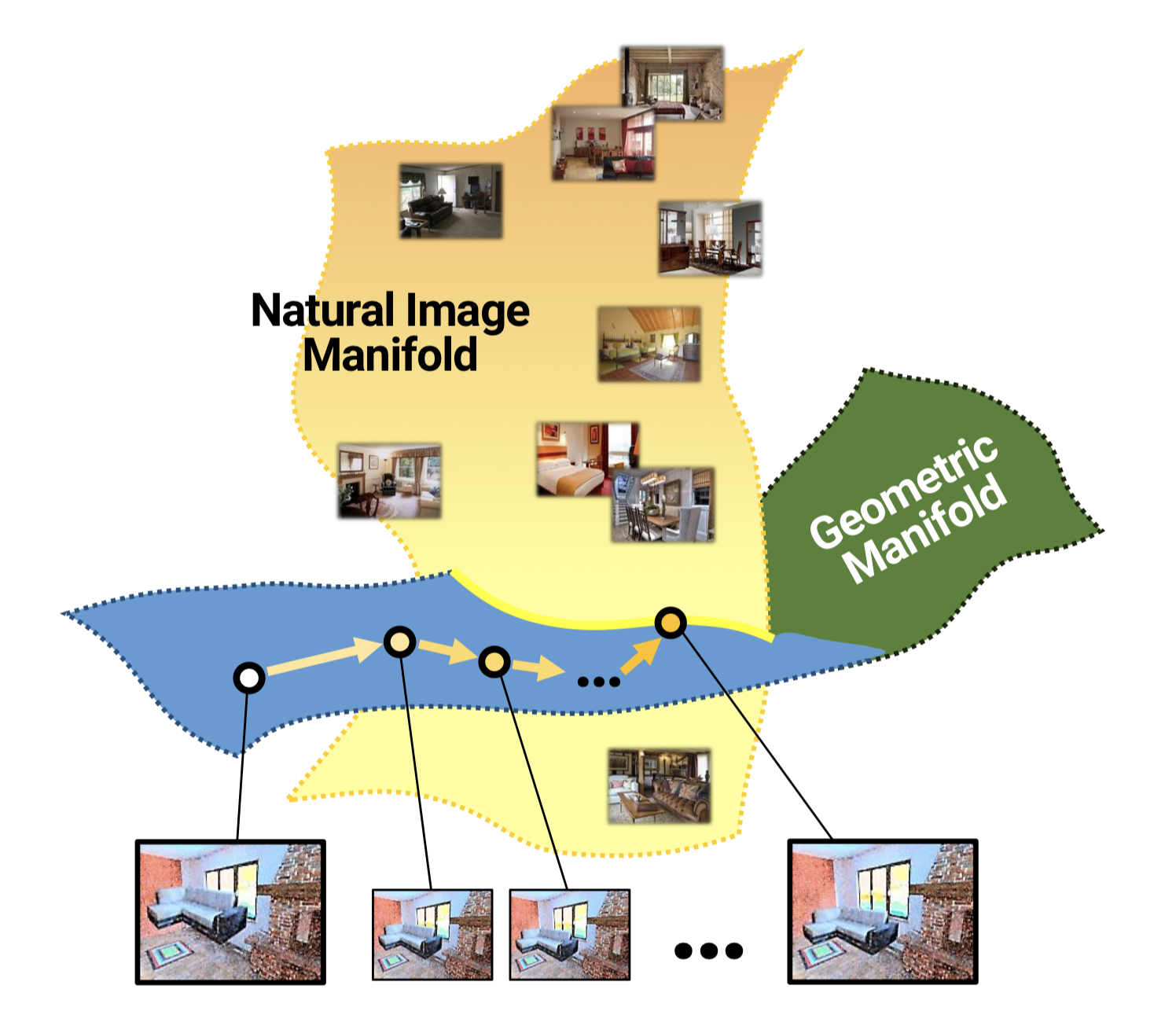
ST-GANの概念的様子。画像に幾何学的処理を加えることで、幾何学的処理が生成する画像の表現空間と現実の画像の表現空間の交点に画像を落とし込む。
ST-GANの構造としては、生成器$G$によって、背景画像と前景オブジェクト画像を入力として前景オブジェクトの幾何学変換の変換因子を推定し、実際に前景オブジェクトを背景画像に配置した1枚の画像を識別器$D$によって識別する、という構造となります。
また生成器$G$では、複数のSTNsを用いることで複数の変換パラメータを逐次的に求めることとなります。
2. Related Work
省略
3. Approach
目標としては、背景画像 $I_{\rm BG}$ と前景オブジェクト $I_{\rm FG}$ (とそれに対応するマスク $M_{\rm FG}$ ) が与えられた際に、前景オブジェクトを背景画像に合成することとなります。その際に、自然な合成となるように前景オブジェクトに対して変換(座標移動や拡大縮小、歪みを加えるなど)を行います。
$$
\begin{eqnarray*}
I_{\rm comp} &=& I_{\rm FG} \odot M_{\rm FG} + I_{\rm BG} \odot (1 - M_{\rm FG}) \
&=& I_{\rm FG} \oplus I_{\rm BG}
\end{eqnarray*}
$$
これは、最初に求める変換パラメータを $\boldsymbol{p_0}$ とすると、以下のように書き換えることができます。
$$
\begin{eqnarray*}
I_{\rm comp} (\boldsymbol{p_0}) = I_{\rm FG} (\boldsymbol{p_0}) \oplus I_{\rm BG}
\end{eqnarray*}
$$
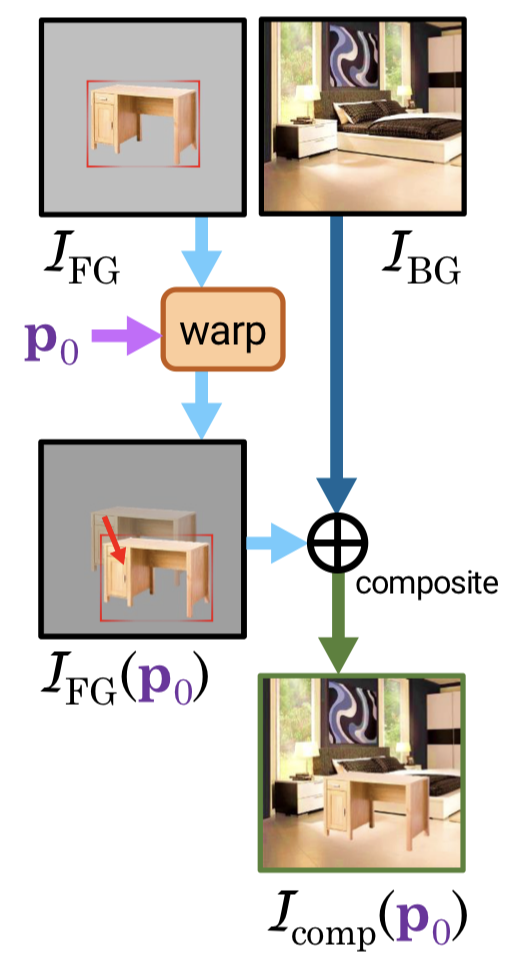
画像合成の概略図。$I_{\rm FG}$ に対して変換パラメータ $p_0$ を元に変換を作用させたのち、$I_{\rm BG}$ と合成する。
なお本研究では複数のSTNsを利用して変換パラメータを反復的に求め、最終的な変換を以下のように定義しています。($\circ$ は変換の合成を表します)
$$
\begin{eqnarray*}
\boldsymbol{p_N} = \boldsymbol{p_0} \circ \Delta \boldsymbol{p_1} \circ \Delta \boldsymbol{p_2} \circ ... \circ \Delta \boldsymbol{p_N}
\end{eqnarray*}
$$
また本研究では変換として射影変換のみを対象に扱います。これは前景オブジェクトを用意する際にある程度姿勢が近いものを用意することを前提としています。
3.1. Iterative Geometric Corrections
ステップ1での生成器$\rm G_1$による $\Delta \boldsymbol{p_1}$ 生成の様子は下図(b)のようになります。背景画像と前景オブジェクト画像(パラメータ$\boldsymbol{p_0}$により変換済)を入力として生成器$\rm G_1$に入力することで、前景オブジェクトの幾何学変換の変換因子$\Delta \boldsymbol{p_1}$を推定します。
また、一連の変換を反復的に求める様子は下図(c)のようになります。$i-1$までに求めた変換を元にステップ$i$で変換因子$\boldsymbol{p_i}$を求める式は以下の通りです。$I_{\rm FG}$についてこれまでのステップで求めた変換$\boldsymbol{p_{i-1}}$を元に変換を行い、その画像と$I_{\rm BG}$を生成器$\rm G_i$に入力することで次の変換$\Delta \boldsymbol{p_i}$を求める、という流れになります。
$$
\begin{eqnarray*}
\Delta \boldsymbol{p_i} &=& {\rm G_i} (I_{\rm FG} (\boldsymbol{p_{i-1}}) , I_{\rm BG}) \
\boldsymbol{p_i} &=& \boldsymbol{p_{i-1}} \circ \Delta \boldsymbol{p_i}
\end{eqnarray*}
$$
(b) STNsを用いて変換パラメータを出力する概略図。$I_{\rm BG}$ 及び、変換パラメータ $\boldsymbol{p_0}$ によって変換させられた $I_{\rm FG}$ を入力にとり、生成器$\rm G_1$ により変換パラメータ $\Delta \boldsymbol{p_1}$ を出力する。
(c) 反復的にSTNsを使用していく様子。直前までの変換パラメータを使用して $I_{\rm FG}$ を変形させ、それと $I_{\rm BG}$ を入力として次の変換パラメータを出力する。
1つの生成器で直接変換パラメータを求めるのではなく複数の生成器を用いて反復的に変換パラメータを求める理由についてですが、大きな変換パラメータを予測することは難しく、先行研究でもこのように反復的に小さな変換を積み重ねた予測を行っているからだそうです。論文中には記述されていませんでしたが、複数のSTNsを構築することで性質の異なる変換(アフィン変換と輝度変換、など)を別々のネットワークで扱うことができるので扱いやすくなるような気もしました。この辺りはあまり分解しすぎると局所解に陥る可能性も高まりますが。
3.2. Sequential Adversarial Training
生成器$G$を学習させるためにGANのフレームワークを適用します。これは、
- 生成画像を現実に近づける問題はマルチモーダルな問題であること(例えば、家具配置問題についてベッドが置かれうる箇所は複数箇所存在する)
- 変換パラメータの値は学習データとして存在しないこと
の2点の理由から妥当であると考えられます。また、ST-GANが通常のGANと異なる点としては、
- ST-GANでは生成器$G$は画像ではなく(画像そのものと比較し)低次元の変換パラメータを出力すること
- 識別器$D$ は生成器$G$が出力した変換パラメータそのものではなく変換パラメータを元に合成された画像を入力とすること
が挙げられます。
前述したように、ST-GANでは複数のSTNsを反復的に作用させます。学習する際には、$N$個の生成器$G1$~$G_N$と、共通の識別器$D$を用いてGANのような相互学習を行います。
最初は単一の生成器$G_1$のみの学習から始め、順次$G_2$, ..., $G_N$と学習を進めていきます。
生成器$G_i$の学習を行う際には$G_1$~$G_{i-1}$の生成器は固定しておき、$G_i$の学習のみを行います。その際には、$G_1$~$G_i$により生成した変換パラメータによって合成された画像 $I_{\rm comp} (\boldsymbol{p_i})$ を$D$に入力することとなります。
生成器ごとに別個の識別器を用意することなく共通の識別器を使用する理由についてですが、これは、画像の「現実らしさ」という指標はSTNsの反復の中で変わるようなものではないので、生成器ごとに識別器を作成するよりは、共通の識別器を学習させるほうがよいという判断のもとそうしています。
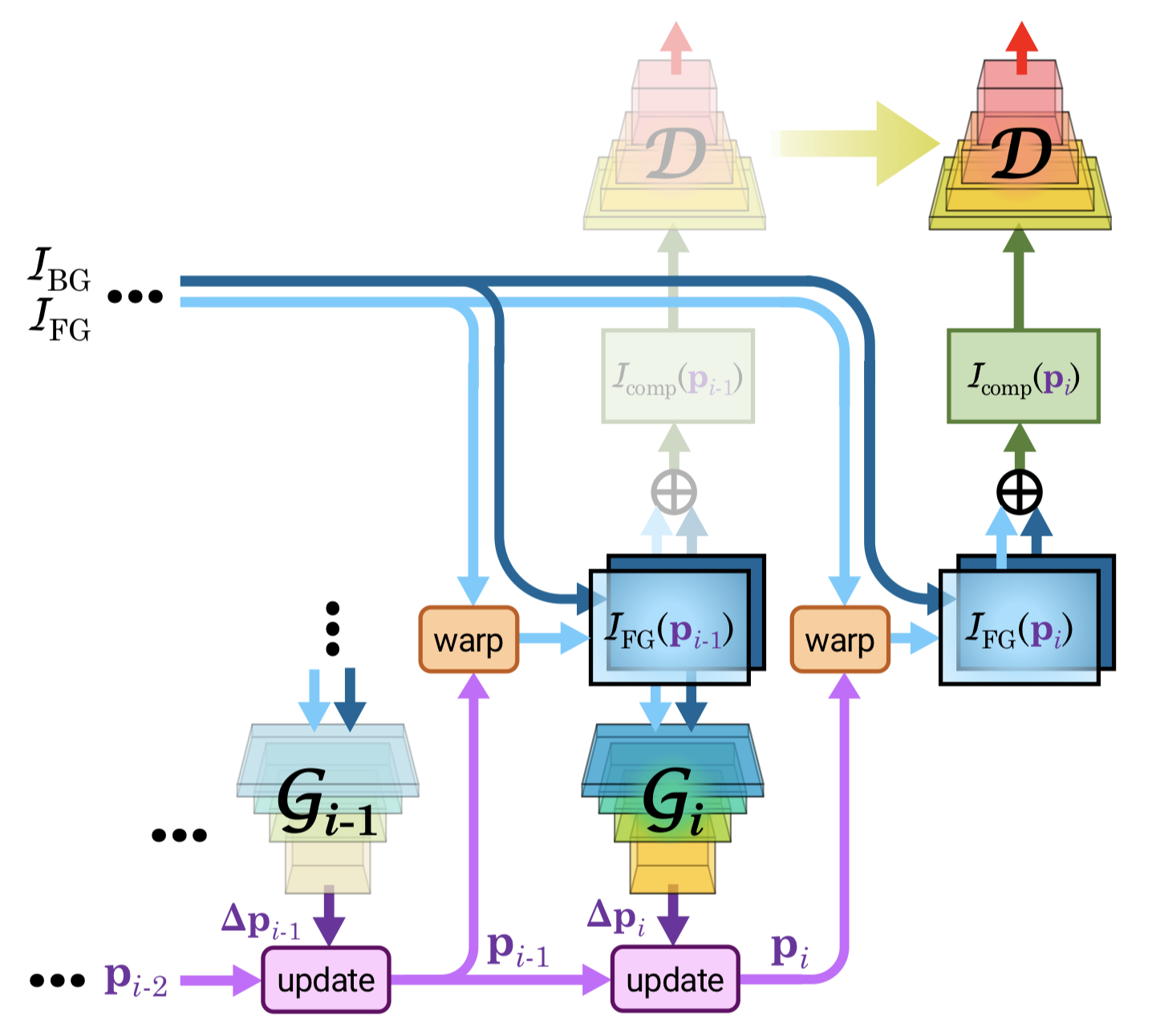
ST-GANの学習の概略図。生成器$G_i$の学習を行う際には$G_1$~$G_{i-1}$の生成器は固定しておき、$G_i$の学習のみを行う。識別器$D$は全ての学習で共通のものを用い、$G_i$の学習時には$G_i$により生成したパラメータによって合成された画像 $I_{\rm comp} (\boldsymbol{p_i})$ を$D$に入力する。
3.3. Adversarial Objective
学習の際にはWasserstein GANに基づいた学習を行います。ステップ$i$での目的関数は以下のように定式化されます。
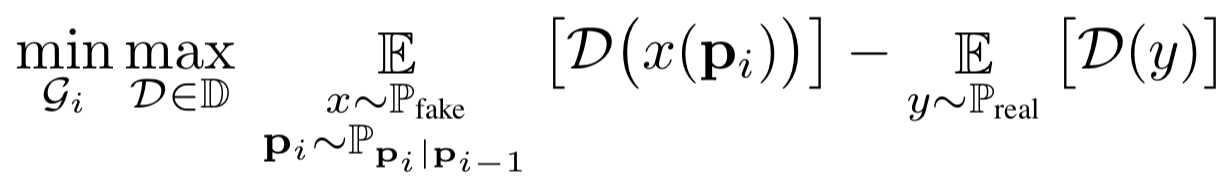WGANでのminimax目的関数。$y = I_{\rm real}$, $x = I_{\rm comp}$ がそれぞれ実データ及び合成した画像を表す。
WGANの性能を改善する手法として [Gulrajani AADC17] らの提案する手法を導入していますが、これについては私自身まだあまり理解していないため省略します。
また、変換パラメータの更新 $\Delta \boldsymbol{p_i}$ について、正則化項 $L_{\rm update} = || \Delta \boldsymbol{p_i}||^2_2$ を導入します。これはST-GANが前景オブジェクトを背景の外に押しやったりオブジェクトを見えないレベルまで収縮したりすることで背景画像のみを残し現実の画像に近づけることを防ぎます。
ST-GANの学習を行う際には、識別器$D$と生成器$G_i$についてそれぞれ以下のような損失関数を用います。$\lambda _{\rm grad}$ 及び $\lambda _{\rm update}$ は正則化項の重みを表す。
識別器$D$と生成器$G_i$それぞれの損失関数。$G_i$及び $\Delta \boldsymbol{p_i}$ については $\boldsymbol{p_i}$ の中に示唆されている。
4. Experiments
Warp parameterizations.
Model architecture.
実験で使用したモデルについて説明します。実験では、生成器及び識別器に入力する画像のサイズは全て120×160にリサイズします(もちろん実際には変換パラメータを推測しているだけなので、テスト画像を生成する際には高画質な画像を生成できます)。
その他のアーキテクチャについては以下の通りになります。
- $\boldsymbol{\rm C} (k)$ : 4×4 のサイズ、$k$個のフィルター、ストライド2のConv-2d レイヤー
- $\boldsymbol{\rm L} (k)$ : $k$個の出力ノードを持つ全結合層
- $G_i$は7チャンネルを入力にとる: 前景オブジェクトのRGBAチャンネル及び背景画像のRGBチャンネル
- $D$は3チャンネルを入力にとる: 合成した画像のRGBチャンネル
生成器$G$、識別器$D$については以下のようなアーキテクチャを用います。$G$については、最終的に射影変換についての8次元の変換パラメータを出力します。
$G$: $\boldsymbol{\rm C} (32)$ - $\boldsymbol{\rm C} (64)$ - $\boldsymbol{\rm C} (128)$ - $\boldsymbol{\rm C} (256)$ - $\boldsymbol{\rm C} (512)$ - $\boldsymbol{\rm L} (256)$ - $\boldsymbol{\rm L} (8)$
$D$: $\boldsymbol{\rm C} (32)$ - $\boldsymbol{\rm C} (64)$ - $\boldsymbol{\rm C} (128)$ - $\boldsymbol{\rm C} (256)$ - $\boldsymbol{\rm C} (512)$ - $\boldsymbol{\rm C} (1)$
$D$についてはPatch-GANのアーキテクチャを踏襲しているそうです(この辺りについてはよく理解できていないので割愛)。
$G$についてはReLU関数を、$D$についてはLeaky-ReLU関数(slope=0.2)を活性化関数として使用しています。
4.1. 3D Cubes
まず、人工的な簡易データを用いてST-GANが実際に適切に幾何補正を加えることができるのか検証します。
6面がそれぞれ適当な単一色で塗られた3Dの直方体の部屋を用意し、面の角度が一致するように内部に3Dのキューブを適当な位置に配置させます。適当な角度からカメラを投影させてできた画像がground-truthとなります。
次に、ランダムな3-DoF変換(前後左右の傾き、回転)を立方体に加え、ランダムな6-DoF変換(3-DoF変換+上下左右奥行きの移動)をカメラに加えます。そうして変形した立方体を前景オブジェクトとして、直方体の部屋を背景画像として別々に描画し、学習データセットとします。
ランダムな射影変換を初期変換 $\boldsymbol{p_0}$ として用いて学習を行った結果を下図に示します。図から分かるように、ST-GANが立方体の歪みや大きさを補正し、実データに近い画像を生成していることが分かります。また、テスト結果の中には、実データとは異なるが自然に見える位置に立方体を落とし込んでいる結果もあり、ST-GANがマルチモーダルな問題に対処できていることが分かります。
(a)データセットの作成例。3Dの直方体の部屋を用意し、中に直方体を配置させる。
(b)ST-GANが立方体に対して適切な変換を施していることがわかる。
4.2. Indoor Objects
次に実用的なデータセットを用いた実験を行います。問題として、室内の画像に家具を配置する問題を扱います。
Data preparation.
SUNCG dataset からデータセットを作成します。SUNCG dataset は45,622件の室内シーンを有し、その中に37カテゴリに及ぶ500万件の3Dオブジェクトが存在します。先行研究にならい、その中から41,499件のシーンと568,749件のカメラ位置を使用します。
室内データ実験における、各カテゴリの3Dオブジェクト数とST-GANの対象に使用した3Dオブジェクトの数。
データセットの作成は下図の手順で行います。
- 対象オブジェクトを一部でも隠すようなオブジェクトを除外する。
- 対象オブジェクトを除外し、それを背景画像とする。
- 元の3D空間についてカメラの角度及び位置を少し変更することで、対象オブジェクトの別角度からの射影を取得する。
- 取得した対象オブジェクトを前景オブジェクトとする。
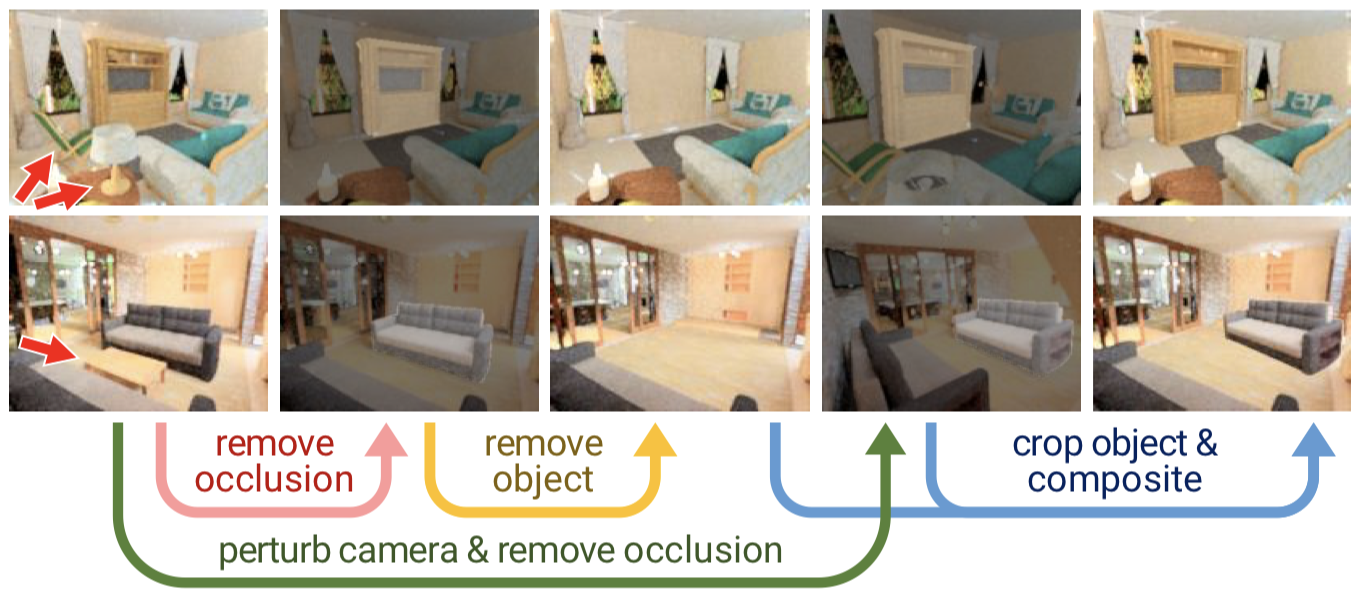3Dシーンから学習データペアを生成する手順。この手順により、前景オブジェクトと背景画像の見え方が一致していないデータペアが作成される。
Settings.
$N = 4$ としてST-GANの学習を行います。初期の変換として、前景オブジェクトをランダムに$0.9$~$1.1$倍に拡大させ、正規分布に従い位置を移動させます。
また、$\lambda _{\rm update} = 0.3$ に設定します。
Baselines.
WIP
Quantitative evaluation.
WIP
Ablation studies.
WIP
Qualitative evaluation.
WIP
4.3. Glasses
データセットがペアになっていないようなタスクとして、人物画像にサングラスを合成するタスクを考えます。つまり学習時に、同じ人物の「サングラスをかけている画像」「サングラスをかけていない画像」が必要でないということを示します。
Data preparation.
CelebAデータセットから、サングラスをかけている人物とかけていない人物の画像を集めます。論文中では学習データとして以下の枚数集めていました。
| 学習データ | テストデータ | |
|---|---|---|
| サングラスをかけていない画像 | 152249 | 18673 |
| サングラスをかけている画像 | 10521 |
さらに前景画像として、10枚のサングラスの透過画像を手作業で作成しています。
用意した画像は下の通りです。
サングラスをかけている・かけていない人物画像(CelebAデータセットから)と、サングラス単体の画像。
Results.
結果は下の画像のようになりました。
全体的に、少し回転するなどしてうまく自然に合成できていますが、初期位置が大きくずれているものについてはあまりうまく合成できていないように思われます。
(a)ST-GANによって自然な方向へ変形していく様子。 (b)様々なサングラスについてうまく合成できている様子。最後の4例については失敗例も含んでいる。
単にもっと良い結果にする方法として、顔のランドマーク(目の位置など)を推定する方法が考えられますが、ST-GANはそのような情報を一切使うことなく予測できています。そのため、ペアデータの取得が難しいような他の画像合成タスクについても予測することができるのではないかと思われます。
5. Conclusion
画像合成のタスクにおいてST-GANは、大規模なデータセットや対でない画像集合に対して従来よりもより現実に近い合成を行うなど、大きな可能性を秘めています。
ST-GANの問題点として、不均衡データや稀な例(例: 白くて太いフレームのメガネ)に対してうまく合成することができず、オブジェクトが大きく移動したり回転したりしたときに収束しないことが挙げられます。