頭の中の整理も兼ねて、Haskellの型システムについて述べたM.P.Jones氏による論文Typing Haskell in Haskellについてまとめていきたいと思います。
※少しずつ加筆しています
Section 2 : Preliminaries
最初のIntroductionは省略させていただきました(興味があったらぜひ読んでみてください)
ここでは早速Haskellのコードが出てきますね。
まず
module TypingHaskellInHaskell
import Data.List (nub,(\\),intersect,union,partition)
import Control.Monad (msum)
とありますね。
まあここは説明しなくてもお分かりでしょう。
型推論器を書く上で用いるのは、Preludeの関数と上記のimportした関数のみです。
次にこのようなプログラムが出てきます。
type Id = String
enumId :: Int -> Id
enumId n = "v" ++ show n
enumIdは整数を受け取って新しい識別子を生成する関数です。
この関数は新しく型変数を生成する際などに用いられます(Section 10で出てきます)
ちなみにIdという型が新しくStringのエイリアスとして定義されていますが、これは識別子を表す型です。
また、型変数の名前は"v"から始まるものとします。
Section 3 : Kinds
ここではkind(高階型)を表すデータ構造について述べられています。
kindは次のように表現されます
data Kind = Star | Kfun Kind Kind deriving Eq
Starは具体型のことですね。
ghci等を開いて:k Maybeなどと打ち込んでみるとたぶん* -> *と表示されると思います。
この表示された内容の*がStarに相当する内容ですね。
ちなみに今、Maybeを例に出してStarの解説をしましたが、Maybeをこのデータ構造を用いて表すと次のようになります。
Kfun Star Star -- * -> *
Kfunは* -> *の->に相当するものです。
Maybeのような場合ではStarを2つ用いれば表すことができましたが、例えば* -> * -> *などの場合はどうでしょう。Kindのフィールドは2つしかないのでStarが3つあるこの高階型は表せないような感じがしますね。
このような場合は次のように表すことができます。
Kfun Star (Kfun Star Star) -- * -> * -> *
Starが4つや5つになっても次のように表せます
Kfun Star (Kfun Star (Kfun Star Star)) -- * -> * -> * -> *
Kfun Star (Kfun Star (Kfun Star (Kfun Star Star))) -- * -> * -> * -> * -> *
簡単ですね、何個でも増やすことができます。
Section 4 : Types
このセクションでは普通の型についての定義などについて述べられています。
型は次のようなデータ構造によって表されます。
data Type
= TVar Tyvar
| TCon Tycon
| TAp Type Type
| TGen Int
deriving Eq
data Tyvar
= Tyvar Id Kind
deriving Eq
data Tycon
= Tycon Id Kind
deriving Eq
それぞれの値コンストラクタが何を表しているかについて説明します。
まず、TVarは型変数を表しています。
型変数とは未確定の型を表す変数です、とりあえずここでは型を含むことのできる変数程度に認識しておいてください。
また、Tyvarでは型変数の変数名と型変数が持つkindを表しています。
次に、TConは型コンストラクタを表しています。
これも型コンストラクタ名と型コンストラクタのkindを持つTyconをフィールドに持ちます。
TApは型適用です。
例えばkind* -> *を持つ型コンストラクタlistがあるとします。
これに型Intを適用して型list Intを作る動作のことです。
この動作は、上のデータ構造を用いて
(TAp (TCon (Tycon "list" (Kfun Star Star))) (TCon (Tycon "Int" Star)))
と表すことができます。
TGenは実体化される前の型とでも考えてください。
どういうことかというと、TGenは例えば次のような型定義があるとします。
id :: a -> a
例えばこの関数にInt型の値を渡すとします。
すると、この関数idの型は
id :: Int -> Int
となります。
Int型でaが実体化されてると言えますね。
このようにパラメトリック多相な関数は関数が表れるたびに、実体化されて用いられるわけです(これについては後で詳しく述べます)
このaがTGenなのです。
つぎに組み込みの型についての定義があります。
tUnit = TCon (Tycon "()" Star) -- ()
tInt = TCon (Tycon "Int" Star) -- Int
tFloat = TCon (Tycon "Float" Star) -- Float
tChar = TCon (Tycon "Char" Star) -- Char
tInteger = TCon (Tycon "Integer" Star) -- Integer
tDouble = TCon (Tycon "Double" Star) -- Double
tList = TCon (Tycon "[]" (Kfun Star Star)) -- [] (* -> *)
tArrow = TCon (Tycon "->" (Kfun Star (Kfun Star Star))) -- -> (* -> * -> *)
tTuple2 = TCon (Tycon "(,)" (Kfun Star (Kfun Star Star))) -- (,) (* -> * -> *)
tString = list tChar -- [Char]
これはきっと上の説明を読んでいただけた方ならどのような事柄を表しているか、理解できると思います。
次にこれらの型を扱う上で必要な、サポート関数の定義です。
infixr 4 `fn`
fn :: Type -> Type -> Type
a `fn` b = TAp (TAp tArrow a) b
list :: Type -> Type
list t = TAp tList t
pair :: Type -> Type -> Type
pair a b = TAp (TAp tTuple2 a) b
fnはa型とb型を取ってa -> b型を作る関数
listはt型を取って[t]型を作る関数
pairはa型とb型を取って(a,b)型を作る関数です。
次に上記の型についてのデータ構造からkindを抜き出す処理です。
class HasKind t where
kind :: t -> Kind
instance HasKind Tyvar where
kind (Tyvar _ k) = k
instance HasKind Tycon where
kind (Tycon _ k) = k
instance HasKind Type where
kind (TCon tc) = kind tc
kind (TVar u) = kind u
kind (TAp t _) =
case kind t of
(Kfun _ k) -> k
これは簡単ですね。
TApの場合の処理について引っかかった方もいるかもしれないので、具体例を上げて説明してみます。
次のような型があるとします。
s = TCon (Tycon "[]" (Kfun Star Star))
-- s :: * -> *
この型に型を適用してみましょう。
TAp s tInt
これをkind関数に渡してみると
kind (TAp t _)
とマッチし次に
case kind t of
でsがkindに渡されます。
そして
(Kfun _ k) -> k
によりKfunの2つ目のフィールドが取り出されています。
なぜ2つ目のフィールドなのかというと、TApで適用されているからです。
2つ目しか取り出さないので* -> *というkindがあるとすると、*、つまり具体型になりますね。
ここでは適用した結果のkindを取り出すのです。
Section 5 : Substituation
Substituationとは、型変数から型への写像です。
Haskellのプログラム中では次のように表されます。
type Subst = [(Tyvar,Type)]
型変数とそれに対応する型のTupleのListとして表されていますね。
次に空のSubstituationの定義です。
nullSubst :: Subst
nullSubst = []
次に演算子の定義が出てきますね。
(+->) :: Tyvar -> Type -> Subst
u +-> t = [(u,t)]
これは型変数uと型tを受け取りSubstituationを作る演算子です。
次にこのようなクラスの定義が出てきます。
class Types t where
apply :: Subst -> t -> t
tv :: t -> [Tyvar]
apply関数はSubstituationを型変数に適用し、型変数を対応する型で置き換える関数です。
tv関数は受け取った型等に表れる型変数をリストにして返す関数です。
普通の型に対しては次のように定義されます。
instance Types Type where
apply s (TVar u) =
case lookup u s of
Just t -> t
Nothing -> (TVar u)
apply s (TAp l r) = TAp (apply s l) (apply s r)
apply _ t = t
tv (TVar u) = [u]
tv (TAp l r) = tv l `union` tv r
tv t = []
TypesのinstanceのListもTypesのinstanceにしてこれらの関数を適用できるようにしておきます。
instance (Types a) => Types [a] where
apply s = map (apply s)
tv = nub.concat.map tv
簡単ですね。
あと2つこの章ではサポート関数を扱います(少し難しくなってきます)
次は演算子の定義です
infixr 4 @@
(@@) :: Subst -> Subst -> Subst
s1 @@ s2 = [(u,apply s1 t) | (u,t) <- s2] ++ s1
apply (s1 @@ s2) == apply s1 . apply s2
となるようなSubstituationをこの演算子を用いることで生成することができます。
やってることは簡単で、s2の型をs1で適用したものにs1を結合しているだけです。
もう一つ関数があります
merge :: (Monad m) => Subst -> Subst -> m Subst
merge s1 s2 =
if agree
then return (s1 ++ s2)
else fail "merge fails"
where
agree = all (\v -> apply s1 (TVar v) == apply s2 (TVar v)) (map fst s1 `intersect` map fst s2)
まず、agreeでは、
(map fst s1 `intersect` map fst s2)
によってs1とs2に共通する型変数を抜き出しています。
そして
all (\v -> apply s1 (TVar v) == apply s2 (TVar v))
によって共通する型変数すべてにs1とs2を適用した結果が等しいことを確かめています。
そして、このチェックを通るとs1 ++ s2によりSubstituationを結合していますね。
なぜこのチェックが必要なのか
仮にこのチェックをせずに、s1 ++ s2で結合した場合を考えます。
型変数にs1とs2を適用した結果が等しいことが保証されていません。
すると、s1を適用した場合とs2を適用した場合では違った動作をしてしまう可能性が出てくるわけです。
そのような動作をしてしまうと、apply (s1 ++ s2)とapply (s2 ++ s1)の結果が違ってしまいます(先に出てきた方を型変数に適用するので)
なのでこのチェックが必要なのです。
Section 6 : Unification and Matching
ここでは単一化とmatchingについて説明しています。
まず、単一化とは2つの型、t1とt2に対し
apply s t1 == apply s t2
となるようなSubstituationsを見つける動作のことです。
この論文では、次のようなコードによって実装されています。
mgu :: (Monad m) => Type -> Type -> m Subst
varBind :: (Monad m) => Tyvar -> Type -> m Subst
mgu (TAp l r) (TAp l' r') =
do
s1 <- mgu l l'
s2 <- mgu (apply s1 r) (apply s1 r')
return (s2 @@ s1)
mgu (TVar u) t = varBind u t
mgu t (TVar u) = varBind u t
mgu (TCon tc1) (TCon tc2)
| tc1 == tc2 = return nullSubst
mgu _ _ = fail "types do not unify"
varBind u t
| t == (TVar u) = return nullSubst
| u `elem` tv t = fail "occurs check fails"
| kind u /= kind t = fail "kinds do not match"
| otherwise = return (u +-> t)
やたら長いコードが出てきましたが、実はこれ、やってる事自体はとても簡単です。
型を辿ってどちらかに型変数が出てきた場合、型変数からもう片方の型へのSubstituationを作っているだけです。
と言われてもいまいちピンとこない方もいるかもしれないので簡単に具体例を出して図説してみます。
例えば次のような整数を二つ受けとり加算する関数があるとします
add :: Int -> Int -> Int
add x y = x + y
そしてこの関数に型が不明な変数xと2を適用してみます
add x 2
この時、xの型は次のように推論されます。
まず、xの型がわからないのでxの型を型変数v0とします。
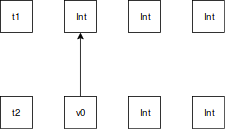
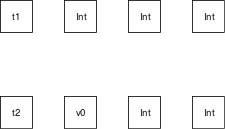
すると、単一化をおこなう関数mguに渡される型は次のように表せます
mguでは型変数が出てきた場合、もう片方の型へのSubstituationを生成するので。
このようにv0からIntへのSubstituationができるわけですね。
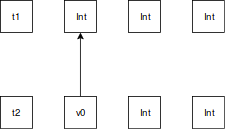
このSubstituationを用いてt2をapplyすると(applyは型変数を対応する型で置き換える関数ですね)
v0はIntに置き換えられてxの型はIntというように推論されます。
このSubstituationを生成するのがmgu関数の役割です。
あと、mgu関数でもう一つ解説しておきたい部分があります。
u `elem` tv t = fail "occurs check fails"
ここでoccurs checkと書いてありますね。
occurs checkとはSubstituationを作る際、型の中に対応する型変数が現れないかチェックすることです。
なぜこのチェックが必要なのかというと定義が無限にループしてしまうからです。
この章ではもう一つ関数が出てきますね。
match (TAp l r) (TAp l' r') =
do
sl <- match l l'
sr <- match r r'
merge sl sr
match (TVar u) t
| kind u == kind t = return (u +-> t)
match (TCon tc1) (TCon tc2)
| tc1 == tc2 = return nullSubst
match _ _ = fail "types do not match"
あれ、この関数、とてもmgu関数に似ていませんか?
何が違うのかというと、mgu関数では(TVar u) tとt (TVar u)どっちのパターンもありましたが、こちらには(TVar u) tのみしかありません。
これはどういうことかというと、第一引数で受け取った型を第二引数で受け取った型に合わせるようなSubstituationを生成するということです。
つまり、この関数はapply s t1 = t2となるようなsを生成する関数ということですね。
Section 7 : Type Classes, Predicates and Qualified Types
このセクションでは型クラスや修飾された型についての実装について述べてあります。