はじめに
ロボット工学の基礎の1つと言えば、順運動学と逆運動学です。任天堂スイッチのソフト「はじめてゲームプログラミング」(以下 はじプロ)を使って逆運動学を解きたいと思います。
今回、関節が2つあるアームロボットをゲーム画面上で出現させ、逆運動学と解いて任意の位置にアームの先を移動させます。ロボットアームは2次元平面上を動くようにして、関節は2つのロボットアームとすることで自由度2の簡易的なモデルとしたいと思います。
まず数式
逆運動学の解き方については「優れた解説サイトがたくさんある」ので、バッサリ数式は省略したいのですが、一般的な式のままだとノードンの機能と一致せず、実装ができません。なので用意されている限られたノードンに、式の方を合わせる必要があります。そういう都合上、(自分の勉強も兼ねて)きちんと解いてみたいと思います。
変数の定義
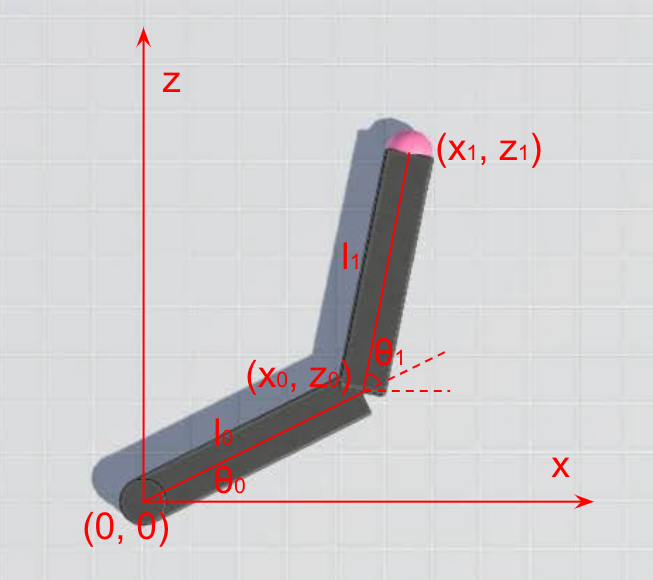
この図と表のように、変数を定義します。
| 変数 | 単位 | 定義 |
|---|---|---|
| $(x_1, z_1)$ | メートル | 原点を(0,0)とする座標系における、目標の位置。はじプロでは真上から床を見ると、軸はxとzの座標になっています。 |
| $l_0, l_1$ | メートル | アームリンクの長さ。固定された根本から順番に0,1と番号を振っています。 |
| $(x_0, z_0)$ | メートル | アーム0とアーム1の間の関節の位置です。 |
| $\theta_0$ | 度 | 原点に対するアーム0の角度。反時計回りの方向が正となっています。範囲は-180〜180。 |
| $\theta_1$ | 度 | アーム0に対するアーム1の角度。そのほかは同上。 |
順運動学
まず、「関節の角度が決まったら、ロボットアームの先端の位置が決まる」という順運動学の式を書きます。
最初に、$(x_0, z_0)$の式。
\begin{align}
\begin{pmatrix}
x_0 \\
z_0
\end{pmatrix}
&=
\begin{pmatrix}
l_0 cos \theta_0\\
l_0 sin \theta_0
\end{pmatrix} \\
&= l_0
\begin{pmatrix}
cos \theta_0\\
sin \theta_0
\end{pmatrix} \tag{1} \\
\end{align}
次に、$(x_1, z_1)$の式。
\begin{align}
\begin{pmatrix}
x_1 \\
z_1
\end{pmatrix}
&=
\begin{pmatrix}
x_0 \\
z_0
\end{pmatrix}
+
l_1
\begin{pmatrix}
cos (\theta_0 + \theta_1)\\
sin (\theta_0 + \theta_1)
\end{pmatrix} \\
&= l_0
\begin{pmatrix}
cos \theta_0\\
sin \theta_0
\end{pmatrix}
+
l_1
\begin{pmatrix}
cos (\theta_0 + \theta_1)\\
sin (\theta_0 + \theta_1)
\end{pmatrix} \tag{2} \\
\end{align}
アーム0に着目すると、$\theta_0$は次のように表せます。
\begin{align}
l_0 tan \theta_0 = \frac{z_0}{x_0} \\
tan \theta_0 = \frac{z_0}{l_0 x_0} \\
\theta_0 = tan^{-1} (\frac{z_0}{l_0 x_0}) \tag{3} \\
\end{align}
同様にアーム1に着目すると、$\theta_1$は次のように表せます。
\begin{align}
l_1 tan \theta_1 = \frac{z_1 - z_0}{x_1 - x_0} \\
tan \theta_1 = \frac{z_1 - z_0}{l_1(x_1 - x_0)} \\
\theta_1 = tan^{-1} (\frac{z_1 - z_0}{l_1(x_1 - x_0)}) \tag{4} \\
\end{align}
逆運動学を解く ①
$\theta_0$を求めるために、$(2)$を変形していきます。
\begin{align}
\begin{pmatrix}
x_1 \\
z_1
\end{pmatrix}
&= l_0
\begin{pmatrix}
cos \theta_0\\
sin \theta_0
\end{pmatrix}
+
l_1
\begin{pmatrix}
cos (\theta_0 + \theta_1)\\
sin (\theta_0 + \theta_1)
\end{pmatrix} \\
\begin{pmatrix}
x_1 - l_0 cos \theta_0 \\
z_1 - l_0 sin \theta_0
\end{pmatrix}
&= l_1
\begin{pmatrix}
cos (\theta_0 + \theta_1)\\
sin (\theta_0 + \theta_1)
\end{pmatrix} \tag{2'} \\
\end{align}
両辺を二乗します。
\begin{align}
\begin{pmatrix}
(x_1 - l_0 cos \theta_0)^2 \\
(z_1 - l_0 sin \theta_0)^2
\end{pmatrix}
&= l_1^2
\begin{pmatrix}
cos^2 (\theta_0 + \theta_1)\\
sin^2 (\theta_0 + \theta_1)
\end{pmatrix} \\
\begin{pmatrix}
x_1^2 - 2l_0 x_1 cos \theta_0 + l_0^2 cos^2 \theta_0 \\
z_1^2 - 2 l_0 z_1 sin \theta_0 + l_0^2 sin^2 \theta_0
\end{pmatrix}
&= l_1^2
\begin{pmatrix}
cos^2 (\theta_0 + \theta_1)\\
sin^2 (\theta_0 + \theta_1)
\end{pmatrix} \\
\end{align}
上下の式を足して、$sin^2 x + cos^2 x = 1$を使って変形します。
\begin{align}
x_1^2 - 2l_0 x_1 cos \theta_0 + l_0^2 cos^2 \theta_0 + z_1^2 - 2 l_0 z_1 sin \theta_0 + l_0^2 sin^2 \theta_0
&= l_1^2 (cos^2 (\theta_0 + \theta_1) + sin^2 (\theta_0 + \theta_1)) \\
x_1^2 + z_1^2 - 2l_0 (x_1 cos \theta_0 + z_1 sin \theta_0) + l_0^2 (cos^2 \theta_0 + sin^2 \theta_0 )
&= l_1^2 (cos^2 (\theta_0 + \theta_1) + sin^2 (\theta_0 + \theta_1)) \\
x_1^2 + z_1^2 - 2l_0 (x_1 cos \theta_0 + z_1 sin \theta_0) + l_0^2
&= l_1^2 \\
2l_0 (x_1 cos \theta_0 + z_1 sin \theta_0)
&= x_1^2 + z_1^2 + l_0^2 - l_1^2 \\
x_1 cos \theta_0 + z_1 sin \theta_0
&= \frac{x_1^2 + z_1^2 + l_0^2 - l_1^2}{2l_0} \tag{5} \\
\end{align}
$R = \sqrt{a^2 + b^2}$, $α = tan^{-1} \frac{b}{a}$ のとき $a cos x + b sin x = R cos(x - α)$ なので
\begin{align}
x_1 cos \theta_0 + z_1 sin \theta_0
&= \sqrt{x_1^2 + z_1^2} cos (\theta_0 - tan^{-1} \frac{z_1}{x_1})\\
\end{align}
これを $(5)$に代入して
\begin{align}
x_1 cos \theta_0 + z_1 sin \theta_0
&= \frac{x_1^2 + z_1^2 + l_0^2 - l_1^2}{2l_0} \\
\sqrt{x_1^2 + z_1^2} cos (\theta_0 - tan^{-1} \frac{z_1}{x_1})
&= \frac{x_1^2 + z_1^2 + l_0^2 - l_1^2}{2l_0} \\
cos (\theta_0 - tan^{-1} \frac{z_1}{x_1})
&= \frac{x_1^2 + z_1^2 + l_0^2 - l_1^2}{2l_0 \sqrt{x_1^2 + z_1^2}} \\
\theta_0 - tan^{-1} \frac{z_1}{x_1}
&= \pm cos^{-1} \frac{x_1^2 + z_1^2 + l_0^2 - l_1^2}{2l_0 \sqrt{x_1^2 + z_1^2}} \\
\theta_0
&= \pm cos^{-1} \frac{x_1^2 + z_1^2 + l_0^2 - l_1^2}{2l_0 \sqrt{x_1^2 + z_1^2}} + tan^{-1} \frac{z_1}{x_1} \tag{6} \\
\end{align}
これで一旦$\theta_0$が求められました。
逆運動学を解く ②
次に$\theta_1$を求めるために、$(2')$の2つの式で割ります。
\begin{align}
\frac{z_1 - l_0 sin \theta_0}{x_1 - l_0 cos \theta_0}
&= \frac{l_1 sin (\theta_0 + \theta_1)}{l_1 cos (\theta_0 + \theta_1)} \\
&= tan (\theta_0 + \theta_1) \\
tan (\theta_0 + \theta_1)
&=
\frac{z_1 - l_0 sin \theta_0}{x_1 - l_0 cos \theta_0} \\
\theta_0 + \theta_1
&= tan^{-1}
\frac{z_1 - l_0 sin \theta_0}{x_1 - l_0 cos \theta_0} \\
\theta_1
&= tan^{-1}
\frac{z_1 - l_0 sin \theta_0}{x_1 - l_0 cos \theta_0} - \theta_0 \tag{7} \\
\end{align}
これで$\theta_1$が求められました。
はじプロの角度に関するノードン
用意されている角度に関するノードンは以下の3つです。
| 名前 | 機能 | 入力 | 出力 |
|---|---|---|---|
角度を位置にノードン
|
入力された角度を位置に変換して出力する。$sin$と$cos$の機能。 | 角度(-180〜180) | ・横位置 ・縦位置 |
位置を角度にノードン
|
入力された位置を角度に変換して出力する。$tan^{-1}$ の機能。 | ・横位置 ・縦位置 |
角度(-180〜180) |
角度の差ノードン
|
入力された2つの角度の差を出力する | ・角度1 ・角度2 |
差 |
そう、 $\theta_0$ の式の中で使っている$cos^{-1}$のノードンはありません。でも大丈夫。 $cos^{-1}$ を $tan^{-1}$ に変形してやれば、位置を角度にノードン を使えるようになりますね。
直角三角形の辺a,b,cが図のような関係のとき、以下の式が成り立ちます。

\begin{align}
\theta
&= cos^{-1} \frac{a}{c} \\
&= tan^{-1} \frac{b}{a} \tag{8} \\
\end{align}
ノードンで表すために式を変形
$(6)$ を $(8)$ のかたちで表すために、 $a, b, c$ を次のようにします。
\begin{align}
a &= x_1^2 + z_1^2 + l_0^2 - l_1^2 \tag{9} \\
c &= 2l_0 \sqrt{x_1^2 + z_1^2} \tag{10} \\
b &= \sqrt{c^2 - a^2} \\
\end{align}
$(6)$ を変形します。
\begin{align}
\theta_0
&= \pm cos^{-1} \frac{a}{c} + tan^{-1} \frac{z_1}{x_1} \\
&= \pm tan^{-1} \frac{b}{a} + tan^{-1} \frac{z_1}{x_1} \\
&= \pm tan^{-1} \frac{\sqrt{c^2 - a^2}}{a} + tan^{-1} \frac{z_1}{x_1} \tag{11} \\
\end{align}
これでノードンで置き換えができる式ができました。
ノードンを使って実装
プログラムのせいり の活用
次に、上記の式をノードンを使って表現していきます。式で使っているたくさんの変数を ワイヤーワープ入口ノードンとワイヤーワープ出口ノードン に置き換えると整理してプログラミングができます。デバッグもしやすい。

私は以下のようにアサインしました。
| 変数 | ワイヤーワープノードン | 説明 |
|---|---|---|
| $\theta_0$ | A | 式(11)で求める |
| $\theta_1$ | B | 式(7)で求める |
| $x_1$ | X | |
| $z_1$ | Z | |
| $l_0$ | L | 実際に作ったアーム0の長さ |
| $l_1$ | M | 実際に作ったアーム1の長さ |
| $a$ | E | 式(9)で求める |
| $c$ | F | 式(10)で求める |
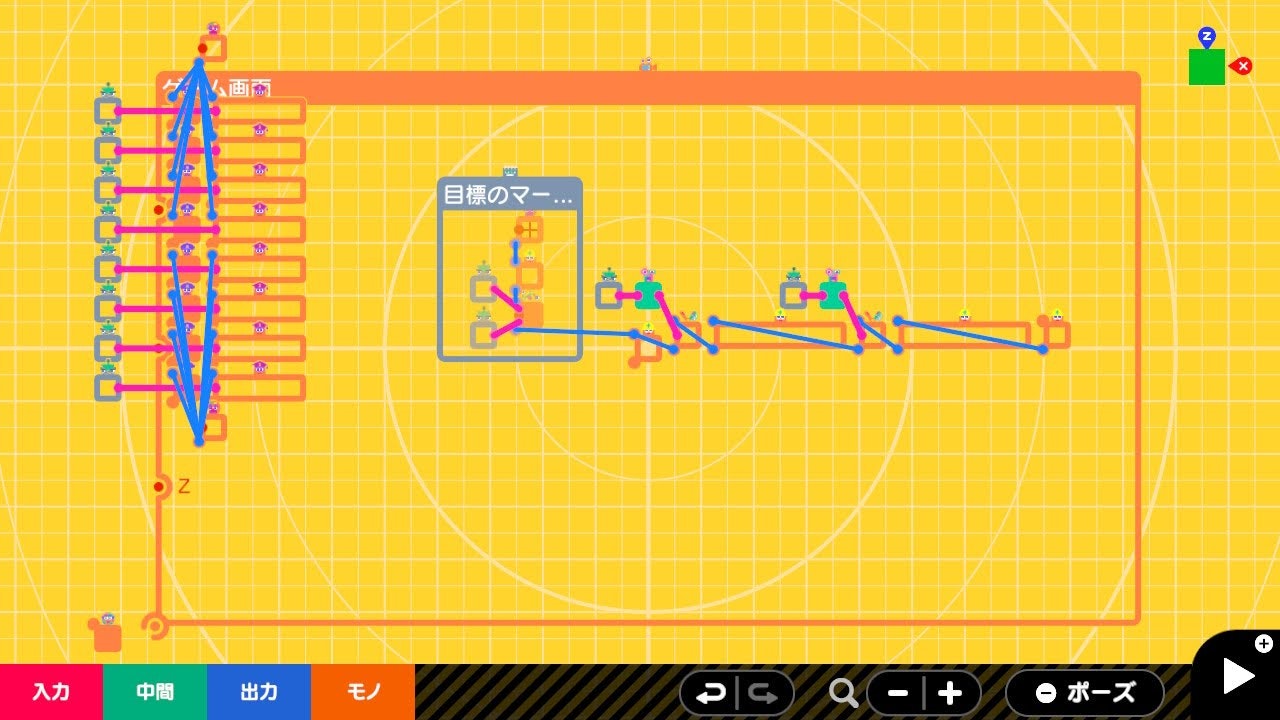
ゲーム画面
ゲーム画面は上から下の床を観る視点に設定しています。中央の(0, 0)の座標にロボットアームの根本(円柱)の中心となるように置きます。
左側に並んでいる8組のノードンたちは、デバッグ用に変数を表示するためのものです。
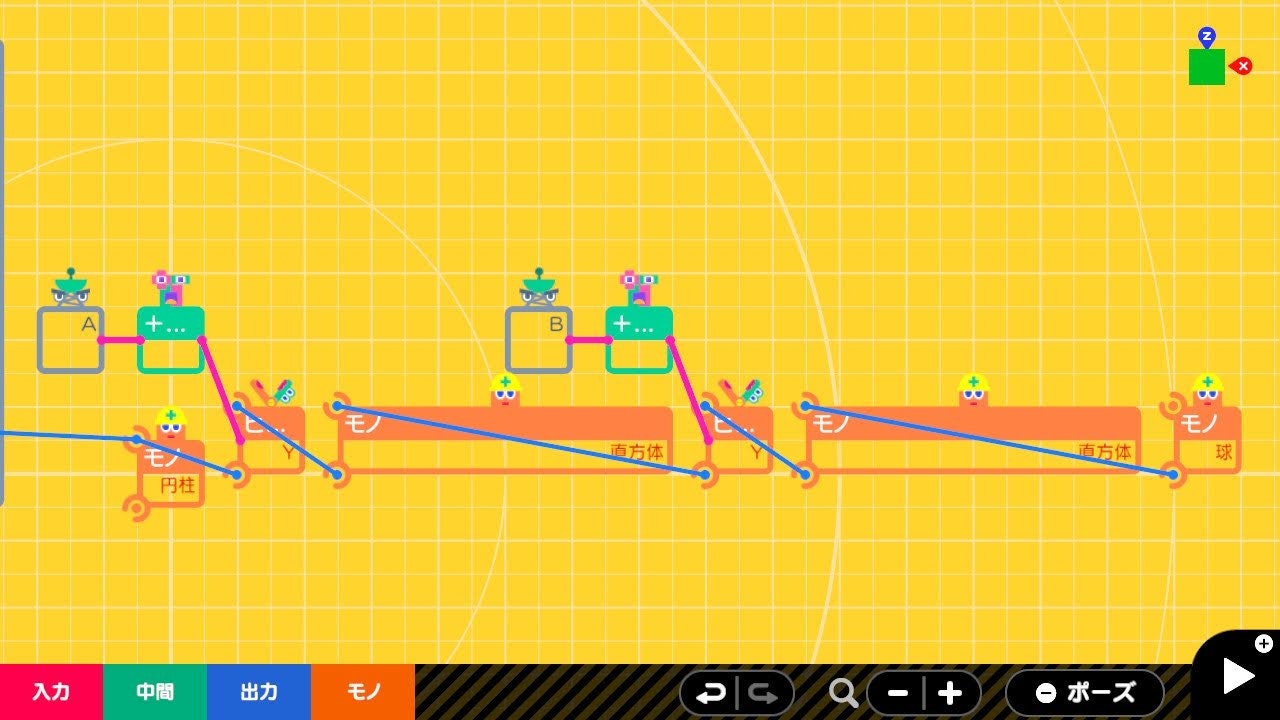
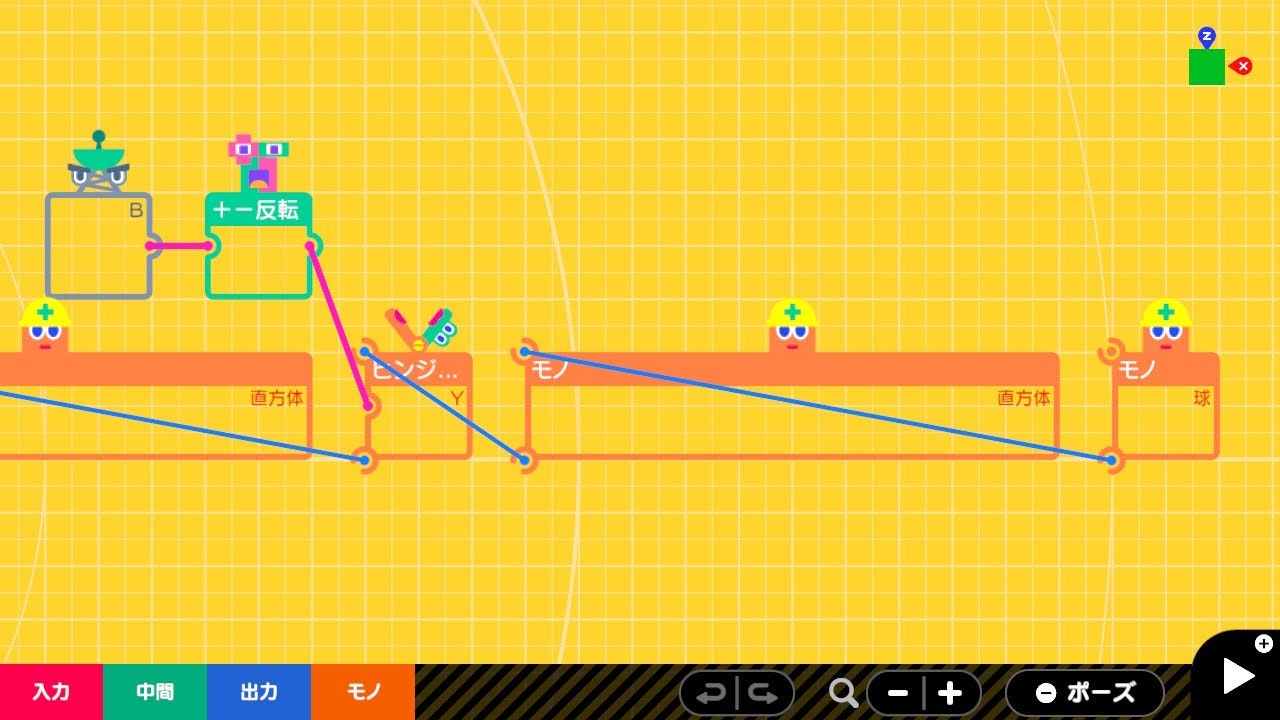
ロボットアーム
| ノードン | 設定 |
|---|---|
| 円柱 | ふるまい : 見える のみ いろ : くろ |
| 直方体 0 | ふるまい : 見える 動く 大きさ X : 4.00 m れんけつ面 : X-→中央 いろ : くろ |
| 直方体 1 | ふるまい : 見える 動く 大きさ X : 4.00 m れんけつ面 : X-→X+ いろ : くろ |
| 球 | ふるまい : 見える 動く れんけつかたさ : バネバネ れんけつ面 : 中央→X+ いろ : ピンク |
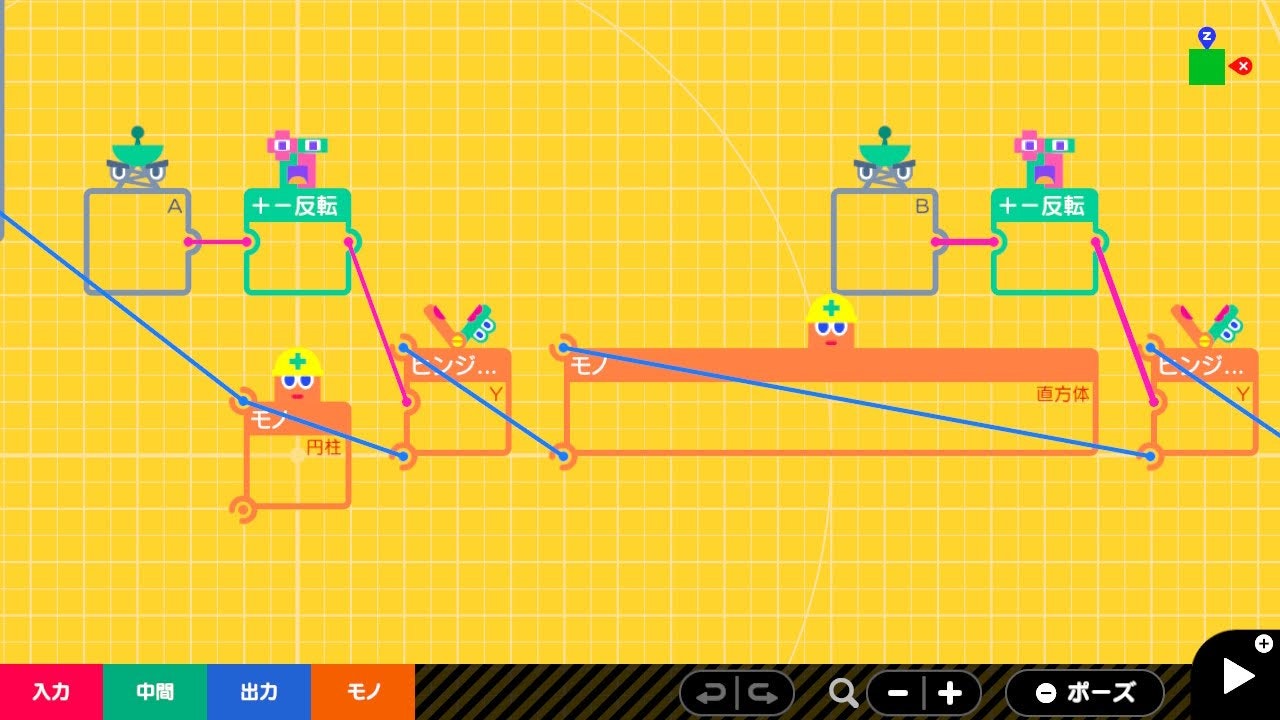
AとBの角度は+ー反転ノードンでプラスマイナスを逆にしています。どうやらヒンジれんけつノードンの回転方向は時計回りになってるようですが、反時計回りにしたいので反転しています。
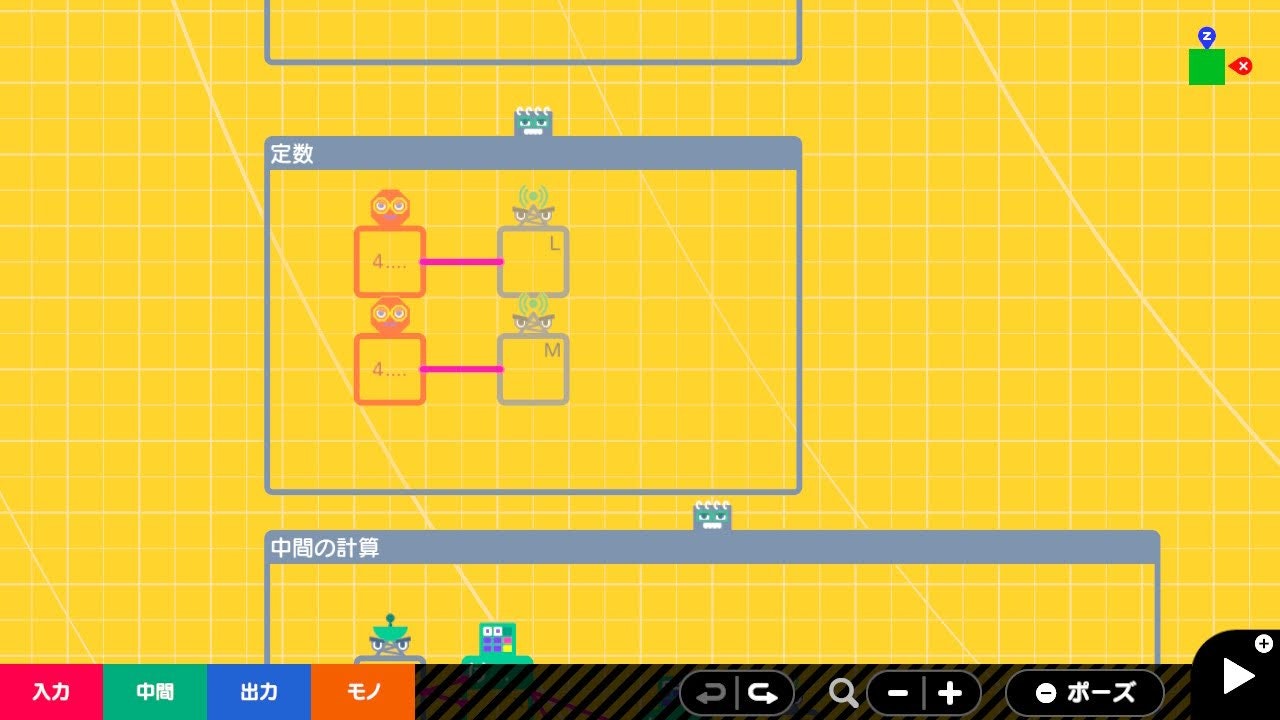
定数
アーム0とアーム1の長さを定数ノードンで設定してます。それぞれ4を設定しています。
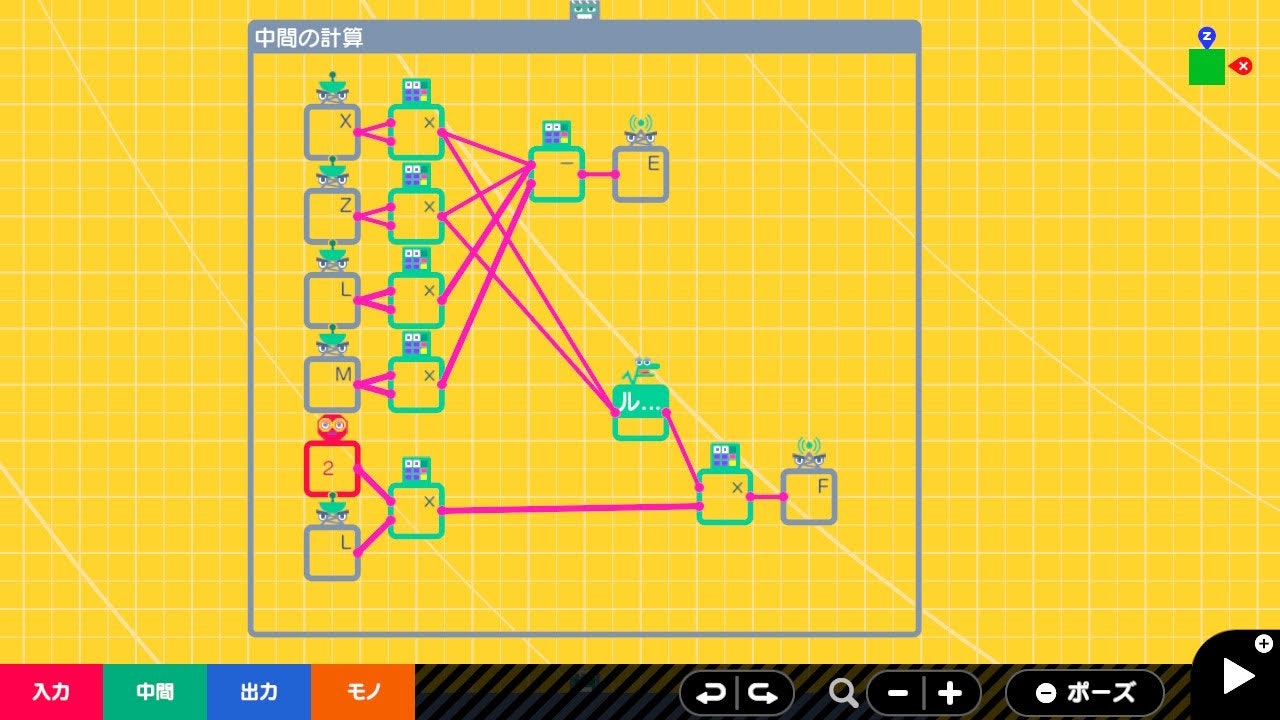
中間の計算
ワイヤーワープノードンEとFに入力するための計算です。使っているのはかけ算、引き算、ルートのノードンです。
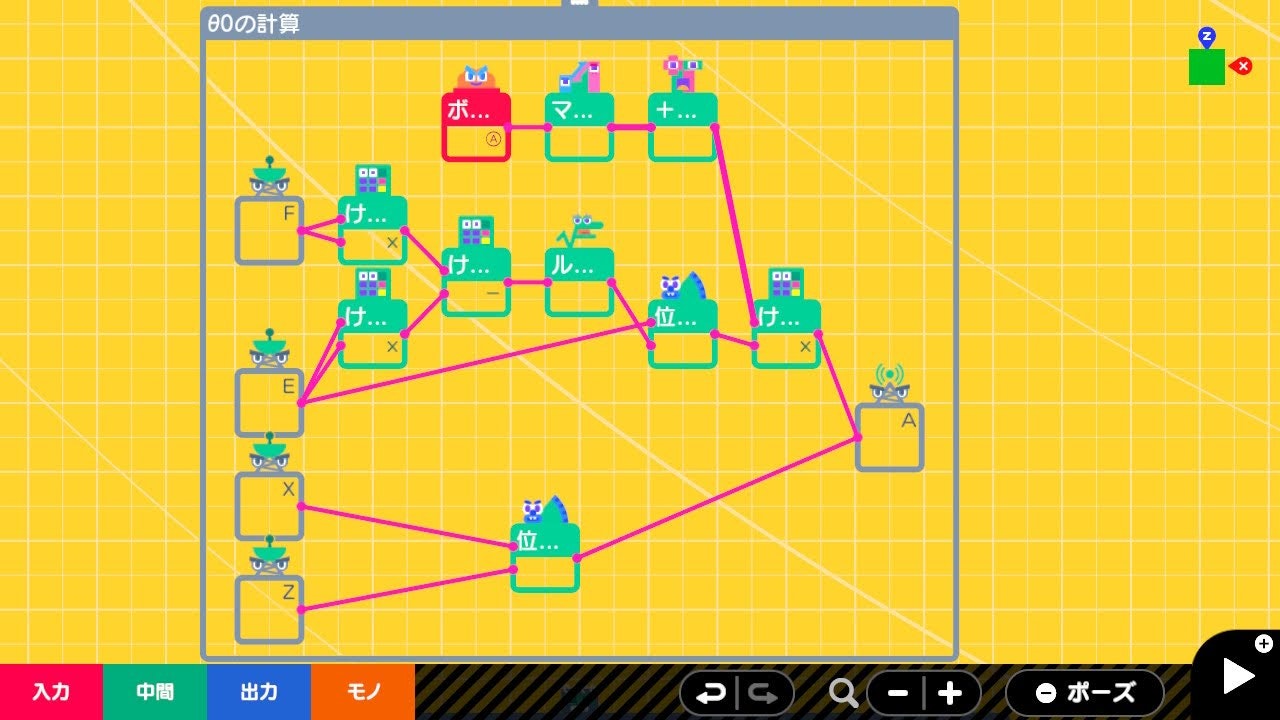
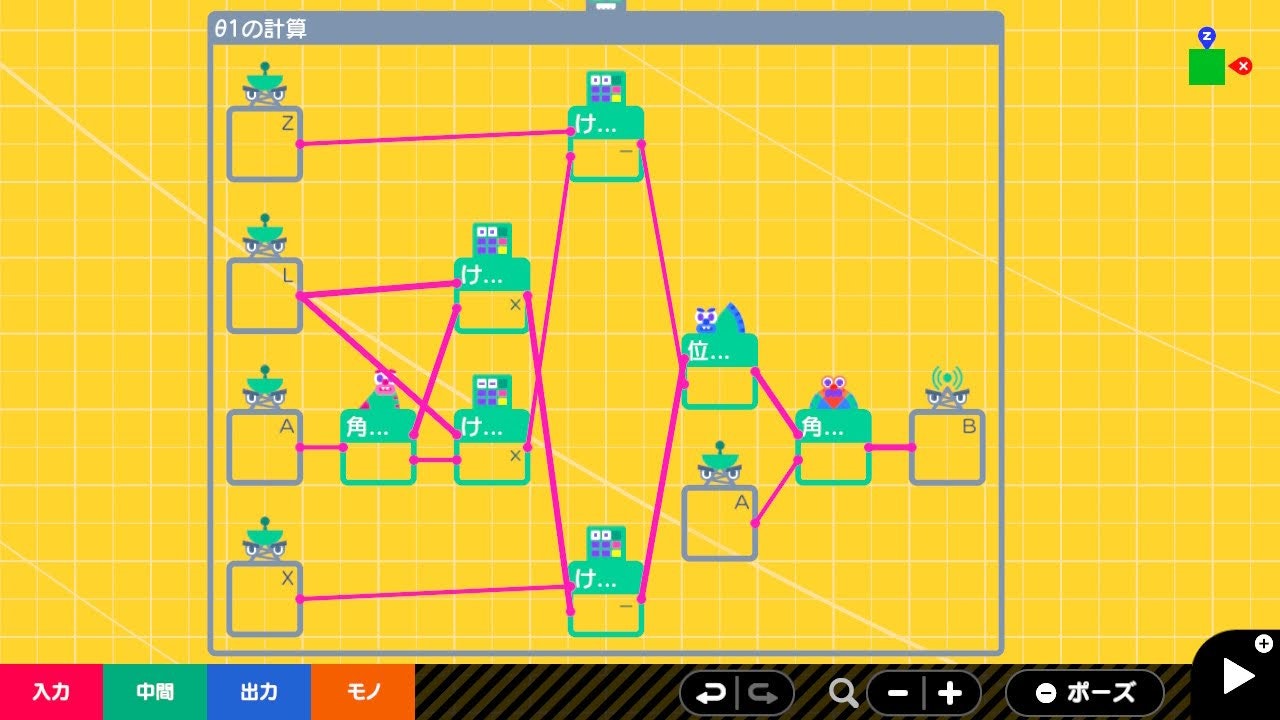
θ0の計算
ワイヤーワープノードンF、E、X、Zを入力し、かけ算、引き算、ルート、位置を角度に のノードンを使って、結果をワイヤーワープノードンAに出力しています。
ボタンAから3つ繋がっている部分は、Aボタン押しで2つ存在する解を切り替える機能を実現しています(デフォルトは+、押すと-)。この流れのノードンの設定は以下のようになっています。
| ノードン | 設定 |
|---|---|
| ボタン | A |
| マッピング | 0-1 → -1-1 |
| +-反転 | |
| けいさん | x |
θ1の計算
ワイヤーワープノードンZ、L、A、Xを入力し、角度を位置に、かけ算、引き算、ルート、位置を角度に、角度の差 のノードンを使って、結果をワイヤーワープノードンBに出力しています。
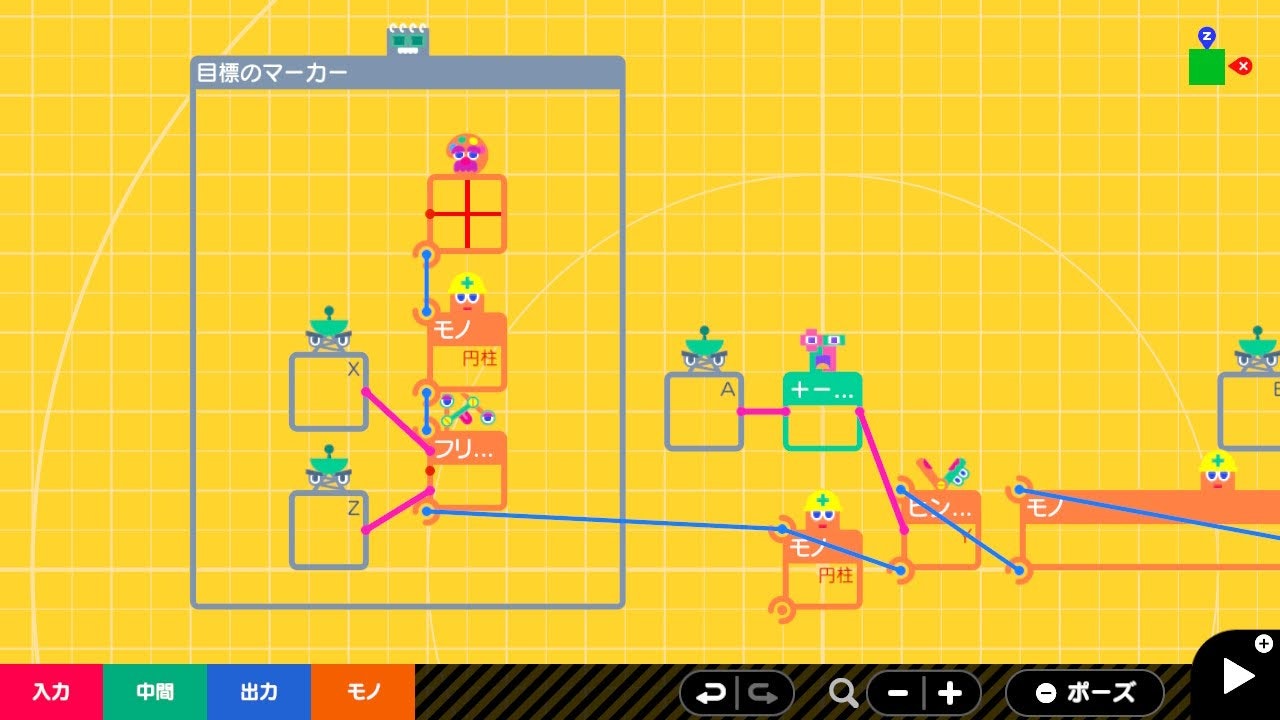
目標のマーカー
アームロボットの根本にある円柱が原点にあるので、これに連結しています。
| ノードン | 設定 |
|---|---|
| フリースライドれんけつ | スライドの移動入力 : XとZ |
| 円柱 | ふるまい : 動く そざい : 無重力 連結面 : Y-→Y+ |
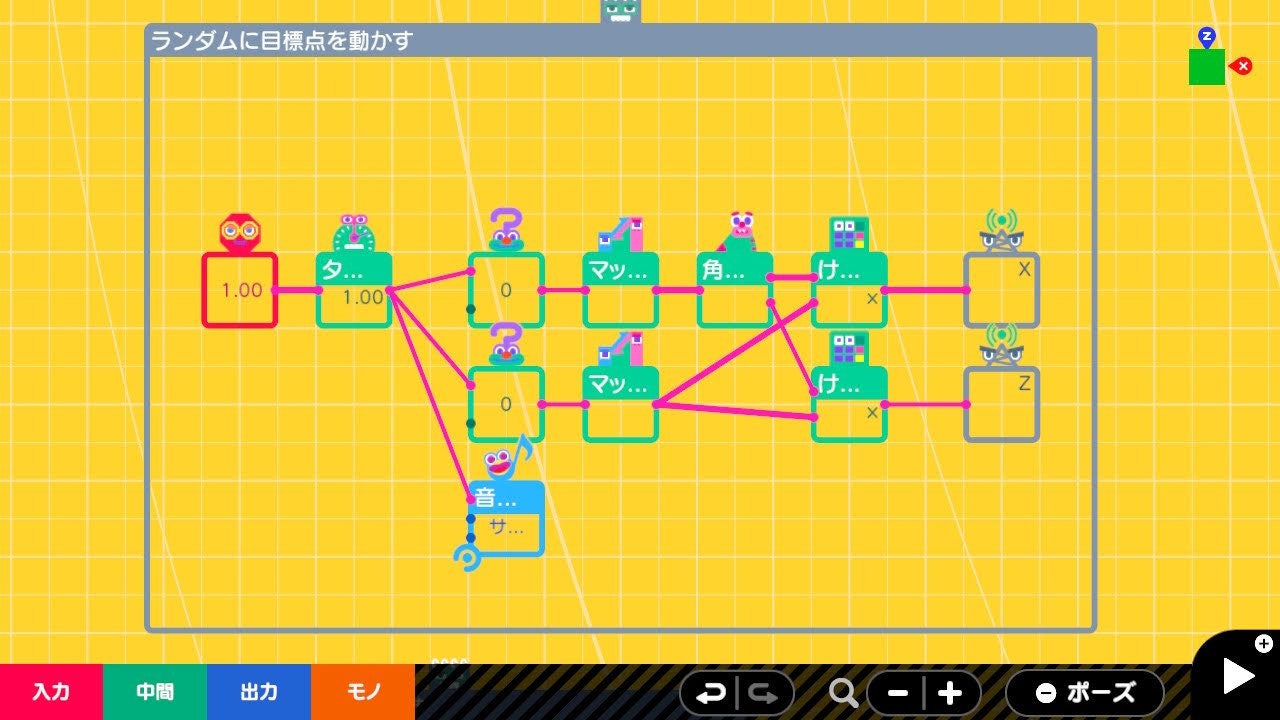
ランダムに目標点を動かす
目標マーカーを1秒間隔でランダムな位置に移動させます。ランダムな半径と角度を変数として、原点から8 m (アーム0とアーム1 の長さの合計)の範囲に目標を置きます。
| 行 | ノードン | 設定 |
|---|---|---|
| 1行目 | タイマー | 1秒間隔 |
| 1行目 | ランダム | 出力はんい : 0-360 |
| 1行目 | マッピング | 0-360 → -180-180 |
| 1行目 | 角度を位置に | |
| 1行目 | けいさん | X |
| 2行目 | ランダム | 出力はんい : 0-100 |
| 2行目 | マッピング | 0-100 → 0.01-8 |
| 1行目 | けいさん | X |
完成
赤い十字マークがランダムに動き、そこを目標にロボットアームの先端が動きます。モーター音を鳴らしながら、目標に向かって吸い付くようにロボットアームが動いていますね。
アームが静止するまで少しゆらゆら揺れるのが良いですね。はじプロでは慣性モーメントがちゃんとシミュレートされているのが分かります。