はじめに
バッチ正規化(Batch Normalization)は深層学習モデルの学習を加速、かつ、安定化させる手段としてよく使われていますが、本記事で取り上げる論文はバッチ正規化なしの新しいアーキテクチャを提案しており、その概要について読んでみましたので紹介します。
- Characterizing Signal Propagation to Close the Performance Gap in Unnormalized ResNet
- ICLR2021
- Paper: https://arxiv.org/abs/2101.08692
(理解不足により記述に誤りが含まれる場合はご容赦ください。)
背景:
バッチ正規化(Batch Normalization)はstate of the artな画像分類器によく使用されています。しかしバッチ正規化が、バッチ内の訓練データ間の独立性を崩し、予期しない弊害を引き起こすこともあります。
本論文のポイント:
本論文では、バッチ正規化層なしで同等性能を実現するモデルNormalizer-Free ResNets(NF-ResNets)を提案しています。大きく下記2点がポイントのようです:
- Signal Propagation Plots(信号伝搬の可視化)
- ReLUにより発生し得るmean shiftを解決するためのScaled Weights Standardizationの提案
提案モデル Normalizer-Free ResNets (NF-ResNets):
本論文では、バッチ正規化層を使用せずにReLUによるMean shiftの問題を解決するため、Normalizer-Free ResNetsを提案しています。
まず、一般的なResNetにおける残差ブロックは方程式:$$x_{l+1} = x_{l} + f_{l}(x_{l})$$のように記載できます。これに対してNF-ResNetsでは、信号伝搬の可視化(ポイント1)の結果に基づき、下記3つの方針に従って残差ブロックを次の方程式のように定義します:$$x_{l+1} = x_{l} + \alpha f_{l}(x_{l}/\beta_l)$$
3つの方針:
- $l$番目の層 $f_{l} (\cdot)$ において、入力と出力の分散が同等になるようにします($Var(f_l (x_l))=Var(x_l)$)。
- 入力$x_l$の分散を正規化する(1にする)スカラー値$β_l$を導入します($β_l=\sqrt{(Var(x_l))}$)。
- $α$ はハイパーパラメータで、ブロック間の分散の増加率をコントロールします。
ポイント1. Signal Propagation Plots(信号伝播の可視化):
残差ブロックを上記のように定義した根拠は、この信号伝播の可視化の結果に基づいています。
下図(a)において、ReLUの後にバッチ正規化をもってきた場合(図の赤い線:ReLU-BN-Conv)には、出力の平均値は0に抑えられていますが、ReLUの前にバッチ正規化をもってきた場合(図の青い線:BN-ReLU-Conv)には、ReLUの特性により、後段の層に行くほど値が増加(mean shift)しています。また図(c)において、ReLUの前にバッチ正規化をもってきた場合(図の青い線:BN-ReLU-Conv)には、出力の分散を1に維持できないことを示しています。要するに、ReLUによるmean shiftを抑え、分散を1に維持することができれば、バッチ正規化層を外しても同じ効果を達成できると言えることになります。
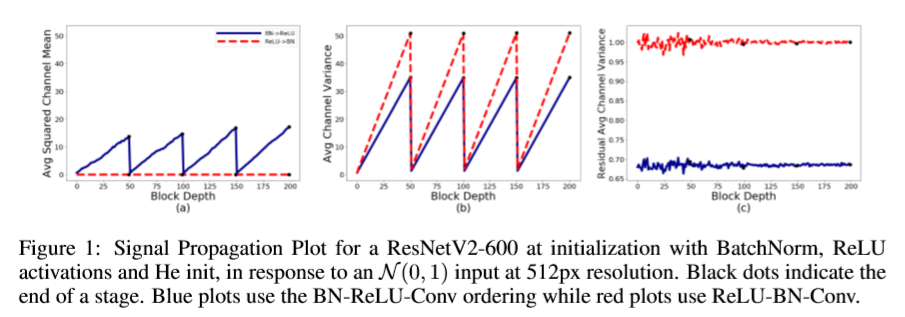
- Average Squared Channel Mean: Mean(Sqrt(Mean(・, axis=NHW)), axis=C)
- Average Channel Variance: Mean(Var(・, axis=NHW), axis=C)
ポイント2. Scaled Weights Standardization:
そこで、ReLUによるmean shiftを抑え、分散を1に維持するためのScaled Weights Standardizationについて紹介します。まずはバッチ正規化層を見ていきます。
Batch Normalization:
$$y=γ \cdot \frac{(x-E[x])}{\sqrt{(Var[x]+ε)}}+β$$
方程式では、入力$x$から期待値$E[x]$(ミニバッチ平均)を引いたものを分子とし、$Var[x]$(ミニバッチ分散)の平方根を分母としています。それにより、バッチ正規化層は出力を平均値0、分散1にコントロールしています。
Scaled Weight Standardization:
$$\hat{W}_{i,j}=\gamma \cdot \frac{w_{i,j}- \mu w_{i, \cdot}}{\sigma w_{i, \cdot}\sqrt{N}}$$
Scaled Weight Standardizationでは、バッチ正規化層と同じ機能を達成できるよう重みのスケーリングを上記方程式のように行っております。見てみると、バッチ正規化層と似ていることが分かると思います。簡単に説明すると、元の重みを平均値$\mu w_{i,\cdot }$で引き、分散$\sigma w_{i,\cdot}\times\sqrt{N}$で割ったものにパラメタ$\gamma$をかけたものになります。
参考)パラメタ$\gamma$の計算 [2]:
ガウス分布に従うノイズ$x$を入力としたとき、ReLUからの出力$(g(x)=max(x, 0))$の分散は
$$σ_g^2=(1/2)(1-(1/π))$$
となります。$Var(W ̂g(x))=γ^2 σ_g^2$のため、分散を1にしたい場合は、
$$γ=\frac{1}{σ_g} =\frac{\sqrt{2}}{\sqrt{1-\frac{1}{π}}}$$
とします。
実験・実験結果:
性能:
本論文では、正則化(Stochastic and dropout)を含む場合と含まない場合の2パターン・5回の実験を行っています。±は5回の実験の標準偏差になります。右から一列目の値が従来のバッチ正規化(BN)を利用したResNetsになります。下記表では、正則化を含む場合は、バッチ正規化層なしのNF-ResNetsの方が、バッチ正規化層ありのResNetsより良い結果を出していることを示しています。
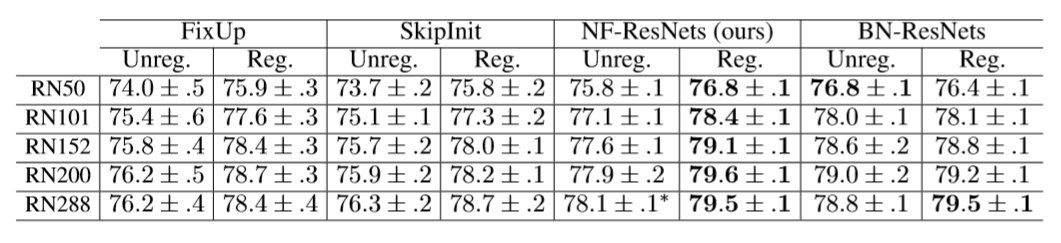
処理時間:
下図では、FLOPs(計算量)の観点でstate of the artのEffcientNetsと同等性能であり、一般的なResNetを大幅に上回っていることを示しています。
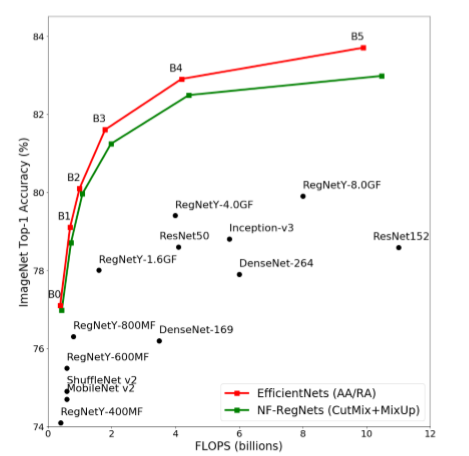
おわりに
本論文で提案した手法は、性能もFLOPsもSOTA同等になっていることを示しており、バッチ正規化層の代替案となり得る手法です。従来の深層学習モデルのアーキテクチャを変えることなく適用できるため、将来的に定番テクニックとなる可能性を秘めていると思います。
以上です。読んでいただき、ありがとうございました。(Written by 王)
参考文献
[1] Andre Brock, Soham De, Samuel L.Smith. Characterizing Signal Propagation to Close the Performance Gap in Unnormalized ResNet. ICLR 2021.
[2] [Devansh Arpit, Yingbo Zhou, Bhargava Kota, and Venu Govindaraju. Normalization propagation: A parametric technique for removing internal covariate shift in deep networks. ICML, pp. 1168–1176, 2016.] (https://arxiv.org/pdf/1603.01431.pdf)