概要
機械学習の手法であるk近傍法(k-nearest neighbor algorithm, k-NN)を使って時系列数値データの異常検知ができないかAmazon SageMakerのビルトインアルゴリズムを使って検証しました。
主に次の2点の観点から検証を行いました。興味があれば一読ください。
- 正常データのみでの学習は可能か
- shingling処理はk近傍法でも有効か
k近傍法って何
k近傍法は機械学習の分類タスクで使用される教師あり学習です。ここではk近傍法がどのような手法なのか簡単に説明します。
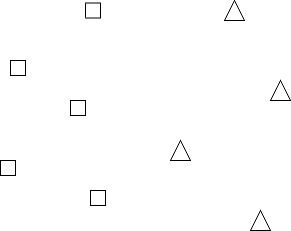
下図のような四角形と三角形が書かれた散布図を使ってk近傍法のアルゴリズムを考えてみます。
少しわかりにくいかもしれませんが、四角グループと三角グループのように既に所属グループがわかっているデータが2次元平面にプロットされている様子だと思ってください。
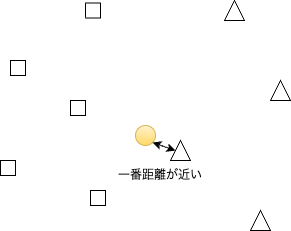
ここでどちらのグループに属するかわからない新たなデータ(黄色い丸)が追加されたとします。
既知の情報からこのデータがどちらのグループに属するのか振り分けを行いたいとします。
おそらく一番近いものと同じグループに入れちゃえばいいじゃないというのが単純に思いつく方法かなと思います。つまり、新たなデータ(黄色い丸)とそれぞれのデータの直線距離を測ってもっとも近いものと同じグループを採用しましょうということです。
今回の場合だと新たなデータ(黄色い丸)は三角グループに属することになります。
でも、ちょっと待ってください。
確かに1番近いのは三角形ですが、2番目と3番目に近いものを見てみるとどちらも四角形です。本当に1番近いものだけをあてにしてしまっていいのでしょうか・・・
k近傍法ではこの点を考慮します。
具体的には事前に設定した値kに沿ってk番目までに近いデータの中で一番多いグループで分類します。
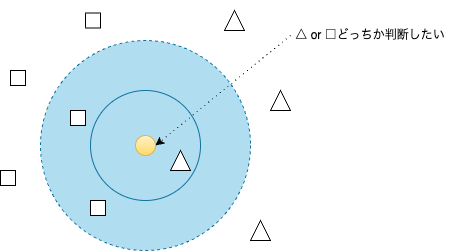
今回は3番目(k=3)までを考慮に入れてみましょう。
わかりやすいように3番目のデータが入る範囲を点線円で囲っています。
すると円(点線)の中にあるデータは四角形が2つ、三角形が1つになりますので新たなデータ(黄色い丸)は四角グループに分類します。
このようにk近傍法では事前に設定した値kに沿ってk番目までに近いデータの中で多数決をして分類を行なっています。
今回このk近傍法を使って数値時系列データの異常検知ができるのか検証してみました。
k平均法と呼ばれる手法もありますがk近傍法とは異なる手法なのでご注意ください。k平均法についてはこちらのブログ記事で紹介しています。
時系列数値データの異常検知
そもそも異常検知とは何かおさらいしましょう。
異常検知(Anomaly detection)とは、膨大なデータの中から他とは違う状態のデータを検出する技術です。具体例として次のようなものが挙げられます。
| 概要 | 具体例 | 対象データ |
|---|---|---|
| 侵入検知 | システムやネットワークで発生するイベントを監視し、侵入を検知 | ログデータ(時系列データ) |
| ビデオ監視 | 設置した防犯カメラから不審者などの侵入を検知 | 画像(時系列データ) |
| 製造不良品 | 製造業で生産される部品などの不良品を画像から検知 | 画像(非時系列データ) |
| スパムメール | スパムメール(チャット)や詐欺メール(チャット)を検知 | メール文(非時系列データ) |
このように異常検知で扱う分野は幅広いため、社会実装への期待が高い技術と言えます。今回は温度や株価といった数値時系列データの異常検知についてk近傍法を使って検証を行います。
時系列データ(time series data)とは、時間に沿って観測されるデータのことを指します。つまり、ある期間にわたって何らかの現象がどのように変化しているかを記録したデータを指します。例えば、株価、気温、人口、売上高、交通量などが時系列データの代表的な例です。
k近傍法は教師あり学習が前提のモデルであり、異常検知を行うモデルとして最適なものとは言えません。しかし、正常データのみでの学習を行ってデータ間の距離を異常度を測るスコアとして考えることによって異常検知に適用できる可能性があります。
そのため今回は正常データのみを学習データとして扱い、ラベルを全て同一のものとして学習を行います。その後、検証データの距離スコア(以下、スコア)をグラフにプロットして異常と想定しているデータのスコアが高くなるか検証を行いました。
具体的には次のようなデータと異常パターンで検証を行いました。
- 乱数データを使用したスパイク異常検知
- 比例データを使用したスパイク異常検知
- 乱数+周期データを使用したスパイク異常検知
乱数データを使用したスパイク異常検知
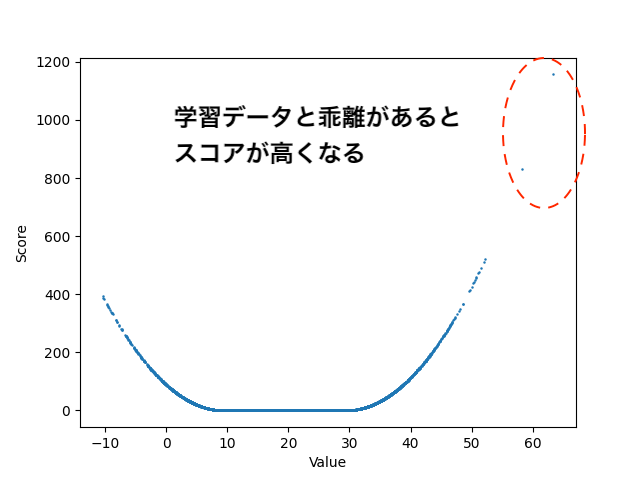
乱数データには学習時に平均20, 標準偏差3の正規乱数10000個発生させて学習を行いました。その後、平均20, 標準偏差10の正規乱数についてスコア計算をすると次のような結果になりました。
学習データに一番近いデータとの距離をスコアとして計算しているので学習データから離れた値ほどスコアが高くなります。
学習に用いたデータは17~23あたりのデータなのでその辺りについてはスコアが低くでていることがわかります。一方で値が60や70になるとかなり高いスコアがでていることがわかります。
まとめ
学習データと比較して極端に大きな値や小さな値についてはスコアが高くなるので閾値を適切に設定することで異常検知することが可能です。
ただ、スコアの閾値設定は人間がするので生のデータに対して閾値設定をするのとあまり差がないと言えます。画像のような複雑なデータであれば別ですが、手間を考えるとあまり実用的ではなさそうです。
比例データを使用したスパイク異常検知
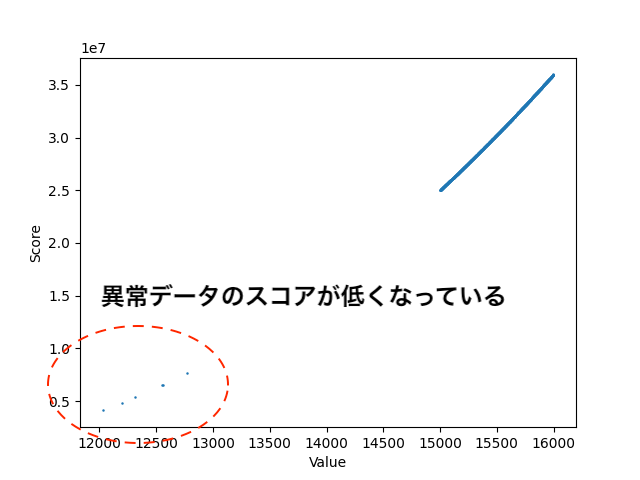
比例データには$y=x$を使用しました。スパイク点についてはいくつかの値の時に$y=0.8x$として計算したものを入れています。
結論からいうとk近傍法ではこちらの異常検知はうまくいきませんでした。異常と想定している値のスコアの方がむしろスコアが低く出てしまっています。
原因は明らかで学習に使用しているデータの方がテストに使用しているデータより値のスケールが小さいためこのような結果になりました。
まとめ
k近傍法はあくまでも学習したデータに一番近いデータとの距離をはかっているだけなので今回のような比例データではうまく検知できませんでした。
仮に比例データの傾きが既知であればデータ変換などの前処理によってある程度異常検知できる可能性はありますが・・・あまり現実的ではありませんね笑
周期データを使用したスパイク異常検知
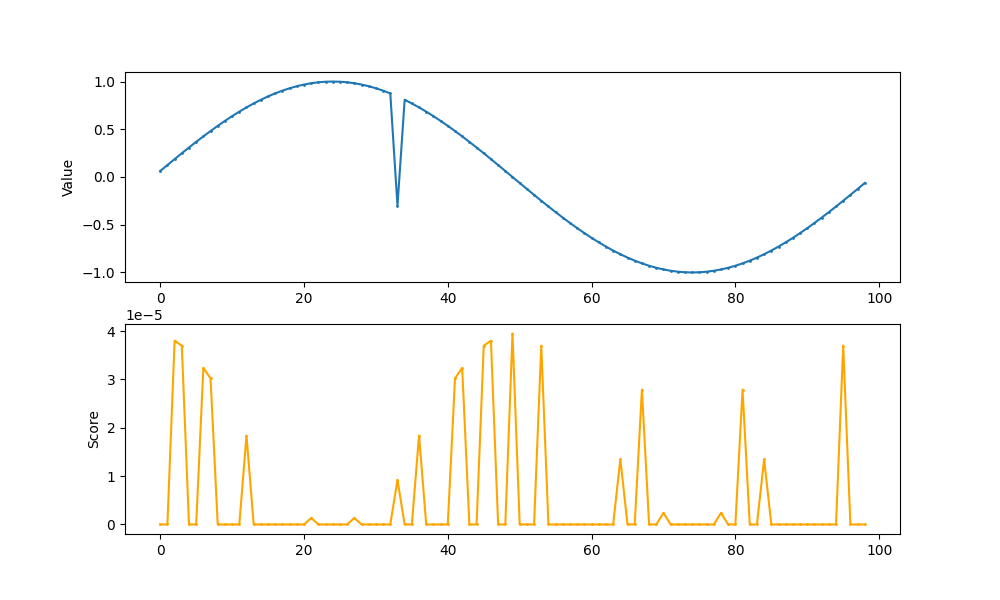
最後に周期データとしてsin関数を使ったデータの学習をしました。ただsin関数を使うだけだとあまりにも現実に即していないのでノイズとして正規乱数を加えたデータを学習データとしています。
また、周期データの異常検知を実施するときに前処理としてshinglingを行なっています。
横軸は時間、青の縦軸は観測データの値、オレンジの縦軸はスコアの値です。sin関数から外れた値でスコアが高くなっていることがわかります。shingling処理を実施しなかった場合はノイズのないsin関数であってもうまくいきませんでした。
このようにshingling処理を行った状態であれば周期データから外れたものを異常として検知できることがわかりました。
追加検証
IoTデバイスでオフィスの温度を計測してより現実的なデータで追加検証しました。
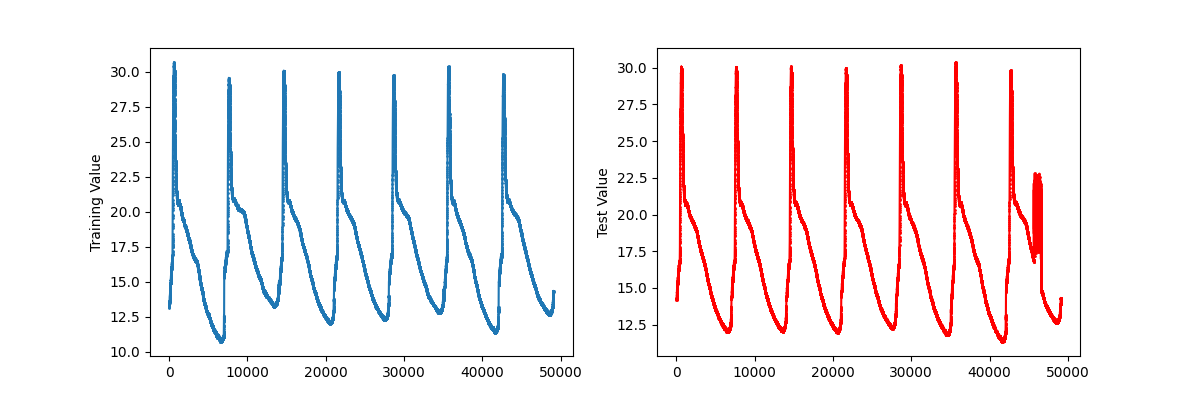
こちらが取得できた5日間のオフィスの温度の時系列データ(左:学習データ、右:テストデータ)です。
5日目の異常を検知できるのか検証してみました。結果は次のグラフ(5日目だけ抽出)です。
5日間と異なる動きをしている部分でスコアが高くなっていることを確認することができました。
最後に
本記事では、k近傍法を用いた異常検知について、いくつかのデータを用いた検証を行いました。
正常データのみで学習を行い、異常度を測るスコアとして算出した距離を利用することで、k近傍法は異常検知に適用できる可能性があることがわかりました。ただし、比例データのようなデータではうまく検知できない場合があることやできたとしても生データに対して閾値を設定することと大差ないような場合があります。
また、k=1として正常系データのみで学習させることに加えてshinglingと呼ばれる前処理を実施することで周期データに対して普段とは異なる挙動を異常として検出できることがわかりました。
モデルの学習サイクルをどうするかといった実運用上の課題はありますが、普段と異なる温度変化を検知できる可能性があるので温度管理が必要な現場で活用できる可能性があることがわかりました。