自動微分に再入門する(1)

概要

数値解析や機械学習を勉強していると必ず出てくる自動微分ですが、理解がかなり怪しかったので勉強しました。

記事の内容としては高校数学や簡単な偏微分は理解しているけど自動微分の概念や実際の操作手順がいまいち頭に入ってこない方向けのものです。

そもそもなぜ微分が必要なのか

微分の必要性について自分視点で書いてみただけなので、読み飛ばしていただいて問題ないです。

例えば古典的な線形回帰モデルを考えてみます。観測値$\left(X_1, Y_1\right), \left(X_2, Y_2\right) \dots , \left(X_N, Y_N\right)$に対して次のような線形関数が成立すると仮定します。

$$
Y_i=\alpha+\beta X_i + \varepsilon_i ,
$$

このときいくつかの強い仮定のもとで、次式を最小にする$\alpha, \beta$の推定値$\hat{\alpha}, \hat{\beta}$は良い性質を持っていることが知られています。¹

$$
S(\alpha, \beta) = \sum_{i=1}^N (Y_i-\alpha-\beta X_i)^2
$$

すなわち古典的な線形回帰モデルは次のような最小化問題として定式化されます。

$$
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}
\hat{\alpha}, \hat{\beta} = \argmin_{\alpha, \beta\in \Theta} S(\alpha, \beta)
$$

今回の式のように目的関数が微分可能であるときは微分することで最小値を与える解を探索することができます。深層学習についても損失関数と呼ばれる目的関数を最小にするようなパラメータを求める問題に帰着します。その際に何度も微分して解を探索します。

ここまでの説明だけだと少しわかりにくいかもしれませんのでもっとシンプルな例で考えてみましょう。

例

次の関数の最小値を求めよ。

$$
f(x) = x^2-6x+10
$$

こんな問題が高校数学で出てくるかなと思います。「平方完成をして頂点を求めて〜」みたいな方法もあるのですが今回の場合だと微分をすることで簡単に答えが求められます。

$$
f'(x) = 2x-6
$$

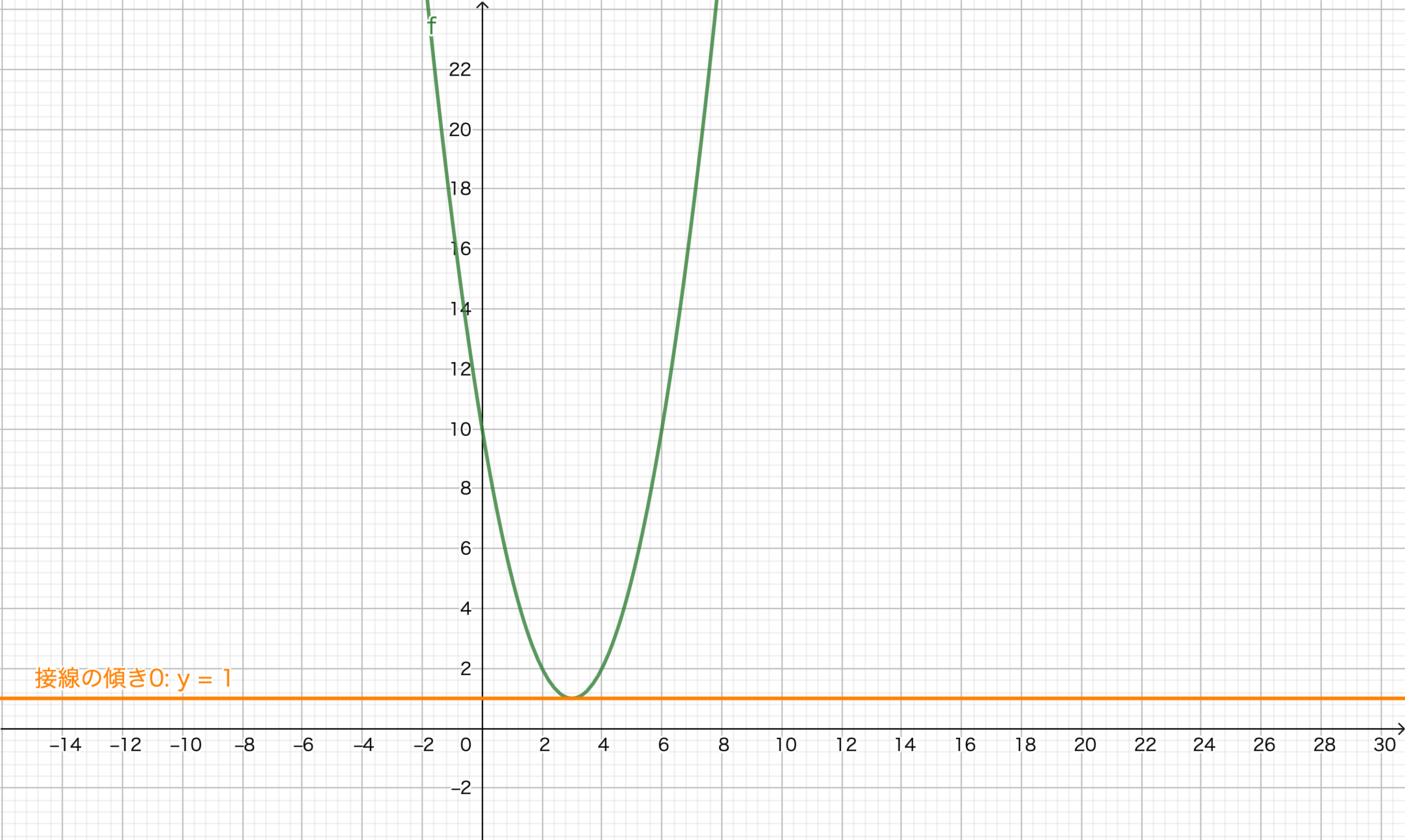
$f'(x)=0$を満たす$x$の値が関数$f(x)$の最小値を与えます。つまり$x=3$の時に最小値$1$になります。²

微分は関数の接線の傾きを表しているので関数の概形が下図のようであれば接線の傾きが$0$、すなわち$x$軸と平行になるところが最小値になります。

このように最適化問題を解く上では微分が強力なツールになります。そのため、コンピュータ上で「微分できる」ことはとても意義があるといえます。

数式微分・数値微分とは

例えば$f(x)=(\sin x+x^3)^2$は微分すれば$2(\sin x+x^3)(\cos x + 3x^2)$となりますが、コンピュータ上で同じことを実現するには例えば数式微分と呼ばれる方法を用います。例えばWolframAlphaで実行すれば同じ結果が得られます。

ただ、私たちは微分した結果の記号$2(\sin x+x^3)(\cos x + 3x^2)$自体が知りたいというよりはむしろ具体的な導関数の値が知りたいことが多く、そのために昔から用いられてきた方法として数値微分と呼ばれるものがあります。これは数値解析の入門テキストに必ず書かれているのでご存知の方も多いかと思います。アイデア自体はシンプルで微分の定義式の極限部分を除いた式を使います。

$$
\frac{f(x+h)-f(x)}{h}
$$

理論的には$h$を調整することで任意の精度で微分を近似することができますが、コンピュータでやるとなると色々問題がでてきます。複雑な式やより高次元の式の場合には計算速度や近似精度に限界がでてきます。

自動微分とは

自動微分では近似式ではなく正確な微分を計算します。基本原理は連鎖律(chain rule) と基本的な微分の結果を使って計算ステップを工夫しています。なお、連鎖律とは次のようなものです。色々書いてますが、高校数学で学習する合成関数の微分法ですね。

$f$を開区間$I$上の微分可能な関数、$g$を開区間$J$上の微分可能な関数とするとき、$g$と$f$が合成可能(つまり> $g(J)\subset I$)ならば合成関数$f \circ g$も開区間$J$上で微分可能であり、導関数は関係式

$$
\left(f \circ g \right)' (x) = f'(g(x)) g' (x)
$$

を満たす。これを連鎖律という。ライプニッツの記法では
$$
\frac{df}{dx} = \frac{df}{dg} \cdot \frac{dg}{dx}
$$
となる。

Wikipedia 連鎖律より引用

自動微分は大きくボトムアップ型自動微分とトップダウン型自動微分の2種類に分かれます。メインはトップダウン型の方ですが、ボトムアップから理解した方がイメージが掴みやすいので順に説明していきます。

ボトムアップ型自動微分

ボトムアップ型自動微分（フォーワードモード、狭義の自動微分）では最初に微分を行う入力変数を固定し、それぞれの部分式を再帰的に計算します。

$$
\frac{\partial y}{\partial x} = \frac{\partial y}{\partial w_1}\frac{\partial w_1}{\partial x} = \frac{\partial y}{\partial w_1}\left(\frac{\partial w_1}{\partial w_2}\frac{\partial w_2}{\partial x}\right) = \cdots
$$

何ともわかりにくいので、例として次の関数で考えてみます。

例

$$
\begin{equation*}
z = f(x_1, x_2) = \left(x_1 + x_2\right)^2 + x_1 x_2
\end{equation*}
$$

簡単な形になるように式を部分的に変数$w_i$で置き換えていきます。やや形式的ですが、まずは$w_1 = x_1, w_2 = x_2$とおきます。

$$
\begin{equation*}
z = \left(w_1 + w_2\right)^2 + w_1 w_2
\end{equation*}
$$

さらに$w_3=w_1+w_2, w_4=w_1w_2$とおくと

$$
\begin{equation*}
z = w_3 ^2 + w_4
\end{equation*}
$$

さらに$w_5=w_3^2, w_6=w_5+w_4$とおくと

$$
\begin{equation*}
z = w_6
\end{equation*}
$$

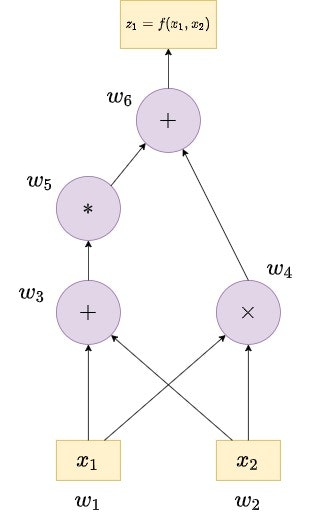
となります。これを計算グラフで書くと次のようになります。四則演算レベルで分解できていることがわかります。

ここからいよいよ自動微分をします。具体的には$w_1, w_2$の微分から初めて逐次的に上位階層の微分を計算していきます。

最初に説明した通りボトムアップ型自動微分ではどの入力変数で微分するかによって初期値が変わってきます。例えば$x_1$での$z$の微分結果を知りたい場合、初期値は次のようになりますが$x_2$での微分結果を知りたい場合は初期値の値が異なるのでその後の計算結果も違うことになり、計算を最初からやりなおす必要があります。

$$
\dot{w}_1 = \frac{\partial w_1}{\partial x_1} = 1
$$

$$
\dot{w}_2 = \frac{\partial w_2}{\partial x_1} = 0
$$

とりあえずやってみましょう。ボトムアップ型自動微分で$x_1$での微分結果は次のように求めることができます。といっても順番に微分しているだけですが・・・

Operations to value	Operations to derivative	result
$w_1=x_1$	$\dot{w}_1 = 1$	seed
$w_2=x_2$	$\dot{w}_2 = 0$	seed
$w_3=w_1+w_2$	$\dot{w}_3 = \dot{w}_1+\dot{w}_2$	$=1$
$w_4=w_1w_2$	$\dot{w}_4 = \dot{w}_1 w_2 + w_1 \dot{w}_2$	$=w_2$
$w_5=w_3^2$	$\dot{w}_5 = 2w_3\dot{w}_3$	$=2(w_1+w_2)$
$w_6=w_4+w_5$	$\dot{w}_6 = \dot{w}_4 + \dot{w}_5$	$=w_2+2(w_1+w_2)$

表の右下が最終的に求めたかった微分の結果です。確かに正しく計算できていることがわかります。

同様に$x_2$での微分結果を知りたい場合は
$$
\dot{w}_1 = \frac{\partial w_1}{\partial x_2} = 0
$$

$$
\dot{w}_2 = \frac{\partial w_2}{\partial x_2} = 1
$$

として計算し直せば求めることができます。

このようにボトムアップ型自動微分は通常の微分をするときと似た感覚で操作することができるので理解することがそこまで難しくありません。その一方で、入力変数の数だけ上記の操作をループする必要があるため入力変数が大量にある関数の勾配を求めるときなどは計算コストが高いです。

次に説明するトップダウン型自動微分では入力ではなく出力変数の個数だけループ処理が必要になってくるので入力変数が多く、出力変数が多いようなケースではトップダウン型自動微分の方がボトムアップ型自動微分よりも効率的です。

トップダウン型自動微分

トップダウン型自動微分（リバースモード、高速自動微分）では、、はじめに微分される出力変数を固定して、それぞれの部分式に関する偏導関数値を再帰的に計算します。 ³

$$
\frac{\partial y}{\partial x} = \frac{\partial y}{\partial w_1}\frac{\partial w_1}{\partial x} = \left(\frac{\partial y}{\partial w_2}\frac{\partial w_2}{\partial w_1}\right)\frac{\partial w_1}{\partial x} = \cdots
$$

先ほどよりもさらに分かりにくいですのでボトムアップ型自動微分で使用した例を使って考えてみましょう。

例1

$w_i$の定義は先ほどと同じですので計算グラフの図自体は同じものです。

ボトムアップ型自動微分では下から上に向かって計算していきましたが、トップダウンでは上から下に向かってグラフを見ていき、分岐している部分式ごとに微分を行っていくような操作をします。

まず、最初は出力変数の1つだけですのでトップの$w_i$である$w_6$に関する微分は$1$となります。

$$
\bar{w}_6 = \frac{\partial z_1}{\partial w_6} = 1
$$

次にグラフが$w_5, w_4$に分岐しているので$w_6=w_5+w_4$を$w_5, w_4$ごとにわけて微分します。これを繰り返します。なお、それぞれ直前の微分の結果も掛けていることに注意してください。

$$
\bar{w}_5 = \bar{w}_6 \frac{\partial w_6}{\partial w_5}=1
$$

$$
\bar{w}_4 = \bar{w}_6 \frac{\partial w_6}{\partial w_4}=1
$$

$$
\bar{w}_3 = \bar{w}_5 \frac{\partial w_5}{\partial w_3}= 2 w_3
$$

最後の$w_1, w_2$は複雑ですがこちらもそれぞれ分解することで微分計算可能です。例えば$w_1$の方を考えてみると$w_1$は$w_3,w_4$と繋がっているので$w_4$と繋がってる部分を$\bar{w}_2^a$, $w_3$と繋がってる部分を$\bar{w}_2^b$として同じように計算します。

$$
\bar{w}_1^a = \bar{w}_4 \frac{\partial w_4}{\partial w_1}= w_2
$$

$$
\bar{w}_1^b = \bar{w}_3 \frac{\partial w_3}{\partial w_1}= 2 w_3
$$

$w_2$についても同様です。

$$
\bar{w}_2^a = \bar{w}_4 \frac{\partial w_4}{\partial w_2}= w_1
$$

$$
\bar{w}_2^b = \bar{w}_3 \frac{\partial w_3}{\partial w_2}= 2 w_3
$$

最後に、別々に計算したそれぞれの$a, b$の値を足します。

$$X_1 = \bar{w}_1^a + \bar{w}_1^b = w_2 + 2 w_3$$

$$X_2 = \bar{w}_2^a + \bar{w}_2^b = w_1 + 2 w_3$$

すると$X_1, X_2$の値が微分した結果になっています。確かに$X_1$の値はボトムアップ型自動微分での$x_1$の微分と一致していることがわかりますね。しかも$x_2$での微分も求められています。

この計算過程からもわかるように出力変数が1つの場合だと勾配計算に費やすループの回数は1回で済みます。つまり、出力変数が入力変数が多いケースだとトップダウン型自動微分の方が計算がはやいことがわかりますね。

参考文献

1. 詳細についてはGauss Markov Theoremを参照してください。私は読んでいませんが、少し前にA Modern Gauss-Markov Theoremも話題になったのでこちらも合わせて参照いただくと良いかもしれません。 ↩

2. もちろんこれは、どんな関数でも微分して0とおけば常にそれが最小値を与える解になると言っているわけではない点に注意してください。関数について仮定があって成立する話です。逆にいうとそういった良い性質を持った関数を考えるように工夫します。厳密な議論は一般的な最適化問題の専門書をはじめ、凸解析や凸最適化の専門書をお読みください。 ↩

3. あとの説明を考慮すると$w$の添字番号を逆にするべきですが、それはそれでややこしくなるのでそのままにしています。なので添字の番号と辻褄が合わないなと思った方はすいませんが読み替えてください。 ↩