注意
本記事は「Atcoder Beginner Contest 148 E - Double Factorial」のネタバレを含みます。この問題を自力で解く予定のある方は閲覧をお控えください。
概要
Atcoderを解いている時にタイトルに関する問題にはまったので、備忘録として残しておくのと、Python有識者の意見を聞きたいがために本記事を投稿します。
問題
Atcoder Beginner Contest 148 E - Double Factorial
0以上の整数nに対し、f(n)を次のように定義します。
・f(n) = 1 [n < 2 のとき]\\
・f(n) = nf(n-2) [n \geq 2 のとき]
整数Nが与えられます。f(N)を10進数で表記した時に末尾に何個の0が続くかを求めてください。
環境
- MacBook Pro(64bit)
- Python 3.8
※AtcoderのPython3のバージョンは「3.4.3」ですが、上記環境でも同様の結果を得られることを事前確認済です。
現象
下記2つのコードで、**上はAC(正解)**となりますが、**下はWA(不正解)**となってしまいます。
import math
N = int(input())
ans = 0
if N % 2 != 0:
pass
else:
for i in range(0, 25):
ans += N // (10 * 5 ** i)
print(ans)
import math
N = int(input())
ans = 0
if N % 2 != 0:
pass
else:
for i in range(0, 25):
ans += math.floor(N / (10 * 5 ** i))
print(ans)
なお、本問題のテストケースは15個ありますが、そのうち下記2つのテストケースでWAとなってしまいました。
[15.txt]
IN: 237590337949089028
OUT: 29698792243636116
[16.txt]
IN: 999003990299500294
OUT: 124875498787437525
予想原因
予想原因は私が原因を特定するまで色々試した内容を綴ったものです。
結果だけ知りたいよ!という方は次の章までスキップしていただけたらと思います。
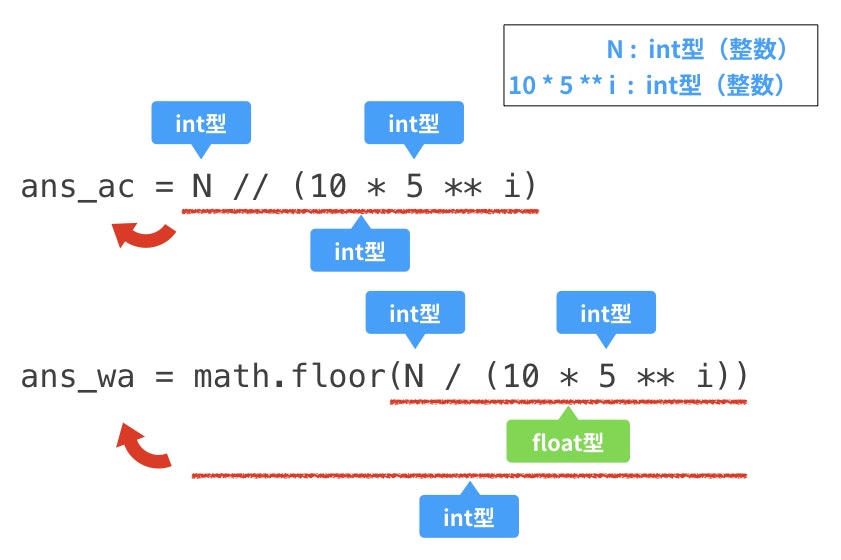
ACとWAに関わるのは下記の部分です。
ans += N // (10 * 5 ** i) #AC
ans += math.floor(N / (10 * 5 ** i)) #WA
両方とも似たようなことをしているので同じ結果になりそうですが、違います。
とりあえず、どこで誤差が生じているのかを出力してみます。下記の通りにします。
※ Nの値はWAとなったテストケース「237590337949089028」を使用します。
import math
N = int(input())
ans_ac = 0
ans_wa = 0
if N % 2 != 0:
pass
else:
for i in range(0, 25):
ans_ac = N // (10 * 5 ** i)
ans_wa = math.floor(N / (10 * 5 ** i))
print('i =', i)
print('d =', N / (10 * 5 ** i))
print('AC:', ans_ac)
print('WA:', ans_wa)
結果は次のようになりました。
i = 0 # 誤差: 2
d = 2.3759033794908904e+16
AC: 23759033794908902
WA: 23759033794908904
i = 1 # 誤差: 1
d = 4751806758981781.0
AC: 4751806758981780
WA: 4751806758981781
i = 2 # 誤差: 0
d = 950361351796356.1
AC: 950361351796356
WA: 950361351796356
i = 3 # 誤差: 0
d = 190072270359271.22
AC: 190072270359271
WA: 190072270359271
(以下省略)
これ以降の繰り返し(iが3以上25未満)はACとWAの誤差が全て0(ACとWAが等しい)でした。
繰り返しの最初(i = 0, 1)だけ誤差が生じていたようです。
とりあえず、このままでは何もわからなさそうなので、違うことを考えることにしました。
ここで一つ頭に思い浮かんだことがありました。これら計算の型は一体どうなっているのでしょうか。
Pythonには実数値を表す型として2つあります。
- int
- float
前者には精度の制限はありませんが、後者にはあります。
問題となっている2つの計算方法はどのような型の偏移をしているのでしょうか。
//に関して、公式ドキュメントによると
x // yxとyの商を切り下げたもの
整数の除算とも呼ばれます。結果の型は整数型とは限りませんが、結果の値は整数です。
結果は常に負の無限大の方向に丸められます。
とあります。ACの計算では一度もfloat型になることなく変数に代入されるようです。
では、WAの計算ではどうでしょうか。こちらはx/yの計算結果によって一度float型を経由しています。
手元の環境で確かめてみました。
A = 4
B = 2
print(type(A), type(B))
print(type(A / B))
print(A / B)
'''
<class 'int'> <class 'int'>
<class 'float'>
2.0
'''
つまり、math.floor()を使う前の時点で既にfloat型になってしまっているのです。
// と math.floor() は似て非なるものなんじゃないか?と考えていましたが、それが原因ではないっぽいです。
公式ドキュメントに載っているmath.floor()の定義については下記の通りです。
x の「床」 (x 以下の最大の整数) を返します。
x が浮動小数点数でなければ、内部的に x.__ floor __() が実行され、Integral値が返されます。
むしろ、WAの計算はfloat型を介したことで、そもそもmath.floor()に適切ではない値を渡していたと予想しました。
型紹介のときに記述しましたが、float型はint型と違って精度の制限があります。
これを調べる方法として次のようなものがありました。
import sys
print(sys.float_info.dig)
# 15
公式ドキュメントは次の通りです。
sys.float_info
float型に関する情報を保持している名前付きタプル
dig: 浮動小数点数で正確に表示できる最大の10進数桁
どうやらfloat型は15桁までは精度がでるが、それ以上の桁は怪しいよということですね...
それでは、先程のWAを出したテストケースを再度確認します。今回は桁数に注目します。
i = 0 # 誤差: 2
d = 2.3759033794908904e+16 # 整数17桁, 少数0桁
AC: 23759033794908902 # 23759033794908904
WA: 23759033794908904 # 17桁 > 15桁
i = 1 # 誤差: 1
d = 4751806758981781.0 # 整数16桁, 少数1桁
AC: 4751806758981780 # 16桁 > 15桁
WA: 4751806758981781
i = 2 # 誤差: 0
d = 950361351796356.1 # 整数15桁, 少数1桁
AC: 950361351796356 # 15桁 = 15桁
WA: 950361351796356
i = 3 # 誤差: 0
d = 190072270359271.22 # 整数15桁, 少数2桁
AC: 190072270359271 # 15桁 = 15桁
WA: 190072270359271
(以下省略)
今回のAtcoder問題の解答は整数桁部分が重要となります。
整数桁がfloat型の精度15桁より多い場合に誤差が生じることが判明しました!
4 <= i < 25のときは整数桁が15桁より大きくなることはないので、誤差が生じることはなかったようです。
誤差が生じたfloat型のdをmath.floor()に噛ませたことで、今回はACがでなかったようでした。
まとめ
-
A // Bとmath.floor(A / B)はやっていることは同じ -
AもBも整数(int)型のときA // Bはそのまま整数型で出力 -
AもBも整数(int)型であってもmath.floor(A / B)はA / Bで浮動小数点(float)型を経由する -
A / Bの結果がfloat型の精度を超えてしまうと誤差が生じてしまう A,Bの値によってはA // Bとmath.floor(A / B)の結果が違うことがある- 競プロでは注意しよう!!
以上になります。ここまでお読みいただきありがとうございました!