1.はじめに
最近、暗号技術の勉強にはまっています。とある本で勉強しているのですが、思ったよりわかりやすくて面白いので、ゆっくりとですが読み進めています。(本については下記に載せておきます)
暗号技術というくらいだから、当然理解が難しいアルゴリズムもあります。しかし、頭の弱い私でも簡単なプログラミングで体験できそうなRSAという暗号技術があったので、Pythonという流行りのプログラミング言語でチャレンジしてみたいと思います。
2.RSAとは?
ふと思ったのですが、2018年に流行った歌の名前に似ていますね。まあ発明者はU.S.Aなので間違いではなさそうです。(本当の本当はイギリスらしいけど)
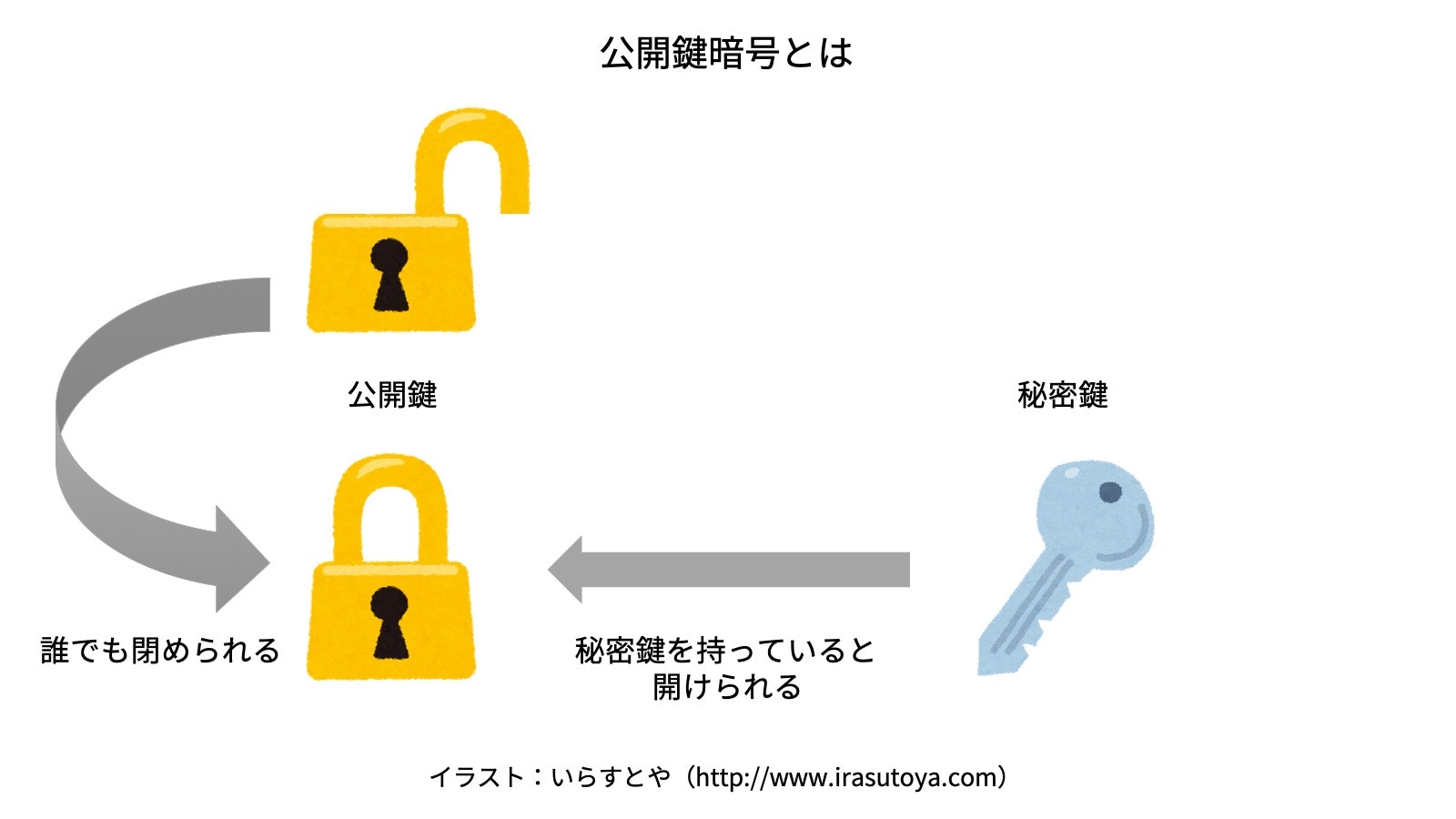
このRSAという技術は、公開鍵暗号アルゴリズムの1つです。この公開鍵暗号について簡単に説明すると、平文の暗号化と暗号文の復号に異なる鍵を用いるということです。ぱっと見意味不明ですが、南京錠をイメージするとわかりやすいです。簡単に図で説明しておきます。ちなみに公開鍵と秘密鍵は両方ともBくんのものです。わかりやすく説明しているQiita記事や文献も多いので詳細は割愛します。
3.RSA暗号体験に必要なもの
次にRSA暗号体験には一体何が必要なのかを整理してみましょう。左の三角形をクリックすると詳細が見られます。
① 平文
上の図でいう「**暗号化されていないAさんの誕生日**」にあたります。これを平文とし、暗号化すると「②暗号文」になります。② 暗号文
上の図でいう「**暗号化されたAさんの誕生日**」にあたります。これを暗号文とし、復号すると「①平文」になります。③ 公開鍵
上の図でいう「**公開鍵**」にあたります。**Bくん**が作成した鍵です。Aさんは、Bくんに渡されたこの公開鍵で「①平文」を「②暗号文」へ**暗号化**します。ちなみに、この公開鍵は他人にバレても**問題ありません。**(だから**公開**鍵)④ 秘密鍵
上の図でいう「**秘密鍵**」にあたります。**Bくん**が作成した鍵です。Bくんは、この秘密鍵で「②暗号文」を「①平文」へ**復号**します。ちなみに、この秘密鍵は他人にバレると**大問題です。**(だから**秘密**鍵)さらに、「③公開鍵」と「④秘密鍵」には次の4つの数字が必要になります。
❶ 数N
N = p \times q\\
となる数Nです。pとqは擬似乱数生成器から得ます。今回は、自分で用意した素数からランダムで得ます。
❷ 数L
L = lcm(p-1, q-1)
となります。
❸ 数E
1 < E < L\\
gcd(E, L) = 1
となります。EとLの最大公約数が1というのは、「EとLとは互いに素」と同意です。
❹ 数D
1 < D < L\\
E \times D \hspace{5pt} mod \hspace{5pt} L = 1
となります。
「文や鍵①〜④」と「4つの数字❶〜❹」でRSAによる暗号化と復号を表すことができます。
暗号化
暗号文 = 平文^E \hspace{5pt} mod \hspace{5pt} N \\
復号
平文 = 暗号文^D \hspace{5pt} mod \hspace{5pt} N \\
「①平文」の暗号化に使われている「❸数E」と「❶数N」が「③公開鍵」
「②暗号文」の復号に使われている「❹数D」と「❶数N」が「④秘密鍵」
「❷数L」は「❸数E」と「❹数D」の作成だけに使用されるので、直接的に暗号化と復号の際には不必要です。
4.PythonでRSAプログラミング!
数式ばかりで嫌になってしまいますが、次に実際にPythonプログラムを書いてみます!「Python3.7」を利用します。
4-1.平文の用意
まずは「①平文」を作りましょう!確かAさんの誕生日でしたね。4月1日でしたから「401」とでもしましょう。この「0」は「月と日の境」を表しています。例えば、2月26日は「2026」、10月9日は「1009」となります。一の位に0を付けて表記しなければ一意に定まるような気がします。最小値は1月1日の「101」、最大値は12月31日の「12031」です。
# 変数名は「birthday」
birthday = 401
4-2.公開鍵の作成
次に「③公開鍵」です。作成には「❸数E」と「❶数N」が必要でした。順を追って用意していきましょう。まずは、「❶数N」を作成するために異なる素数p,qが必要です。本来であれば、擬似乱数生成器で得た数を素数判定して得るものですが、今回はわかりやすく素数配列を用意してそこからランダムで素数を選びたいと思います。このような感じでプログラムを書いてみました。
# 素数配列をそれぞれ準備
p_candidates = [101, 103, 107, 109, 113, 127, 131, 137, 139, 149]
q_candidates = [151, 157, 163, 167, 173, 179, 181, 191, 193, 197]
# randomモジュールの関数でランダムに要素を1つ選択
p = random.choice(p_candidates)
q = random.choice(q_candidates)
# 数Nを作成
N = p * q
素数配列は101~200までの素数20個を10個ずつに分けてあります。(199も素数ですが...) ちなみにこのプログラムで作成される「❶数N」の最小値は、101×151=15251で、14bitで表現できてしまいます。この程度のビット数で暗号した場合、ブルートフォース攻撃等であっという間に解読されてしまうのでダメですね。
次に「❸数E」が欲しいところですが、その前には「❷数L」が必要ですね。p-1とq-1の最小公倍数がこれになるのでした。Pythonのmathモジュール(Python3.5以上)で、最大公約数を簡単に求められるので、これを利用してみます。
# 関数lcmを用意
def lcm(x, y):
return (x * y) // math.gcd(x, y)
# 関数lcmの引数にp-1とq-1を指定しLに代入
L = lcm(p - 1, q - 1)
xとyの最小公倍数は、「xとyをかけあわせた数」を「xとyの最大公約数」で割ることで求めることができます。これを利用しています。//演算子は、浮動小数点数の場合でも演算結果を小数点以下は切り捨てるものです。
「❶数N」と「❷数L」を得られたので、漸く「❸数E」を作成できます! まずは、randomモジュールの関数randrangeで、1より大きく「❷数L」よりも小さな乱数Eを作ります。このEを先ほどの関数gcdを使って「❷数L」と最大公約数が1であるかを確かめます。1であればそのまま。1以外であれば再度乱数を発生させましょう。
# 引数は「2」以上「L」未満の1刻みの乱数発生
E = random.randrange(2, L)
# 最大公約数が1でなければ
while math.gcd(E, L) != 1:
# 再度乱数を発生
E = random.randrange(2, L)
「❸数E」と「❶数N」がなんとかできました!「③公開鍵」は良さそうです。
4-3.秘密鍵の作成
「❶数N」「❷数L」「❸数E」があれば、そのまま「❹数D」もいけます。範囲を2以上「❷数L」未満の範囲で数D候補を繰り返し文で回していき、「❸数E」と数D候補をかけた数をLで割ったときの余りが1であるときに、その数D候補を数Dに確定します。
for i in range(2, L):
if (E * i) % L == 1:
D = i
break
ちなみにこの数D候補は沢山ありますが、Lで割った余りが1になるのは必ず1つしかありません。これで「❹数D」もできたので「④秘密鍵」も完成です!
4-4.平文を暗号文へ
平文の用意、そして公開鍵・秘密鍵の作成もできました。では実際に、公開鍵がBくんからAさんに無事送られたことを想定して、Aさんは自分の誕生日情報(平文)を公開鍵(「❸数E」「❶数N」)にて暗号化します。
暗号化は
暗号文 = 平文^E \hspace{5pt} mod \hspace{5pt} N \\
という単純な数式でできます。E乗はpow関数で簡単に行えます。平文を暗号化したものは変数cipherに代入します。
cipher = pow(birthday, E) % N
これで暗号化することができます! このcipherをAさんからBくんに送ります。
4-5.暗号文を平文へ
AさんからB君へ送られた暗号文cipherは、B君が機密に持っている秘密鍵(「❹数D」と「❶数N」)にて復号することができます!
平文 = 暗号文^D \hspace{5pt} mod \hspace{5pt} N \\
先ほどの暗号化同様の式なので詳しくは省略しますが、これにてAさんがB君に送りたいAさんの誕生日情報を無事に送ることができるはずです。
decipher = pow(cipher, D) % N
暗号文を復号した平文は、変数decipherに代入して、暗号化前の平文である変数birthdayと比較します。
5.暗号化前と復号後を比較
当然、まだ試していないので上記のプログラムが本当に正しいかどうかはわかりません。なのでテストします。pとqの候補が10個ずつなので、100通りの鍵ペアが作成ができます。とりあえず30回くらいループで回してみます。
プログラムはこちらから
import math
import random
# 関数lcmを用意(4-2)
def lcm(x, y):
return (x * y) // math.gcd(x, y)
# Aさんの誕生日(4-1)
birthday = 401
for var in range(0, 30):
# 素数配列をそれぞれ準備(4-1)
p_candidates = [101, 103, 107, 109, 113, 127, 131, 137, 139, 149]
q_candidates = [151, 157, 163, 167, 173, 179, 181, 191, 193, 197]
# randomモジュールの関数でランダムに要素を1つ選択
p = random.choice(p_candidates)
q = random.choice(q_candidates)
# 数Nを作成
N = p * q
# 関数lcmの引数にp-1とq-1を指定しLに代入(4-2)
L = lcm(p - 1, q - 1)
# 引数は「2」以上「L」未満の1刻みの乱数発生
E = random.randrange(2, L)
# 最大公約数が1でなければ
while math.gcd(E, L) != 1:
# 再度乱数を発生
E = random.randrange(2, L)
# 数Dの作成(4-3)
for i in range(2, L):
if (E * i) % L == 1:
D = i
break
# 平文 -> 暗号文(4-4)
cipher = pow(birthday, E) % N
# 暗号文 -> 平文(4-5)
decipher = pow(cipher, D) % N
# 出力 暗号化前平文 -> 暗号文 -> 復号後平文?
print("{0} -> {1} -> {2}".format(birthday, cipher, decipher))
実行結果は次の通り。
# 暗号化前平文 -> 暗号文 -> 復号後平文?
401 -> 18308 -> 401
401 -> 19347 -> 401
401 -> 15326 -> 401
401 -> 11450 -> 401
401 -> 17400 -> 401
401 -> 1274 -> 401
401 -> 3552 -> 401
401 -> 7005 -> 401
401 -> 4425 -> 401
401 -> 21979 -> 401
401 -> 3815 -> 401
401 -> 4370 -> 401
401 -> 24533 -> 401
401 -> 16421 -> 401
401 -> 12949 -> 401
401 -> 20149 -> 401
401 -> 7525 -> 401
401 -> 22536 -> 401
401 -> 1230 -> 401
401 -> 10159 -> 401
401 -> 15164 -> 401
401 -> 2754 -> 401
401 -> 2878 -> 401
401 -> 10722 -> 401
401 -> 3521 -> 401
401 -> 5469 -> 401
401 -> 4969 -> 401
401 -> 5036 -> 401
401 -> 24001 -> 401
401 -> 15078 -> 401
全て無事に「401」が復号できたようです! 無事にBくんはAさんの誕生日がわかりました!
6.感想とか
これだけみるとRSA暗号の仕組みはそこまで難しくないように見えますが、実際に今強固な暗号アルゴリズムとして多くの場所で使われています。今回は簡単な用意した素数だけで試してみましたが、これが膨大な数の素数で同様に行われたらとんでもないな〜と思いました。実際には、これだけではRSAは使えません。上の例なら、本当にBくんがAさんに送った鍵なのか?という問題が発生します。
余談ですが、Aさんの誕生日情報として平文を決めたとき、
最小値は1月1日の「101」、最大値は12月31日の「12031」です。
と記述しましたが、この最大値がNの値をオーバーすると、上のような綺麗な復号ができなくなります。まあその理由については、下で紹介している本を読んでみてください。本当にオススメ。(投げやり)
7.参考文献
- 結城 浩著 『暗号技術入門 第3版 秘密の国のアリス』 SBクリエイティブ株式会社