はじめに
久々にQiitaの記事を書きます。nishiwakkiです。今回は「Pythonその2 Advent Calendar 2020」の「12日目」枠として本記事を投稿します!(投稿、日付変更直前で申し訳ないです... 急いでいたので図の色が全体的に気持ち悪いです)
趣味でPythonを使って、ちょっとした遊び開発だったり、競プロをしたりするのですが、その際にソートをよく利用します。ソートというと、バブルソートやクイックソートなどが頭をよぎりますが、Pythonのソートメソッドsortで使用されるのは一体何ソートなのかな〜? とふと思ったのがきっかけです。
# ソートメソッド sort を実際に使ってみる
l = [5, 1, 3, 4, 2]
print(l) # 出力結果: [5, 1, 3, 4, 2]
l.sort()
print(l) # 出力結果: [1, 2, 3, 4, 5]
「ソートなんて興味ないw」な方や「男は黙ってボゴソートでしょ」という方々も、是非読んでいただけると嬉しいです!
結論からいうと
Pythonで用いられているソートアルゴリズムは、「Timsort」と呼ばれるものだそうです。
(Python公式ドキュメント「Sorting HOW TO」より)
......は?知らんと思ったそこのアナタ、安心してください。私も知りませんでした...(泣)
Timsortのプロフィール
Timちゃんの上から下まで隅々と調査しました。
| 項目 | オーダー | 説明 |
|---|---|---|
| 平均計算時間 | $O(n \log n)$ | ソートにかかる平均的な時間 |
| 最良計算時間 | $O(n)$ | 元の並びが良く最速でソートできた場合の時間 |
| 最悪計算時間 | $O(n \log n)$ | 元の並びが悪くソートに最も長くかかった場合の時間 |
| メモリ使用量 | $O(n)$ | 空間計算量とも。ソートに使用するメモリの量 |
| 安定性 | あり | 同値のデータの順番がソート前・後で変わらない |
ソートの計算量は、最悪計算時間がピックアップされることが多いです。オーダー記法で書いてあるので、難しいと感じる方もいらっしゃると思いますが、他のソートと比較してみるとこんな感じです。
| ソート | 最悪計算時間 |
|---|---|
| バブルソート | $O(n^2)$ |
| クイックソート | $O(n^2)$ |
| Timsort | $O(n \log n)$ |
そして、オーダー記法はこのような速い・遅い関係になっています。
【速】$O(1)$ < $O(\log n)$ < $O(n)$ < $O(n \log n)$ < $O(n^2)$【遅】
Timちゃんは高速なソートアルゴリズムだということですね、優秀!
安定性があるのも嬉しいです!
Timsortの正体
Timちゃんが優秀なのはわかりましたが、一体何者なのでしょうか?
結論からいうと、Timsortは下記2つの有名ソートのハイブリッド(いいとこ取り)です。
2つのソートの詳細については、本記事では省略します。
本記事では、シンプル実装のTimsortを見ていきます!(実際のPythonのsortの実装は複雑です)
Timsortは大きく分けて4つのステップがあります!
- minRunの計算
- minRunをもとに配列を分割
- 分割した配列ごとに挿入ソートを実施
- 分割したソート済み配列にマージソートを実施
【注意】
Timsortを行いたい配列の要素数 $N$ が $N < 64$ の場合、
ステップ2の配列分割は実施されず、入力配列に挿入ソートのみが実施されて終了します。
ステップごとに見ていきます。
STEP1. minRunの計算
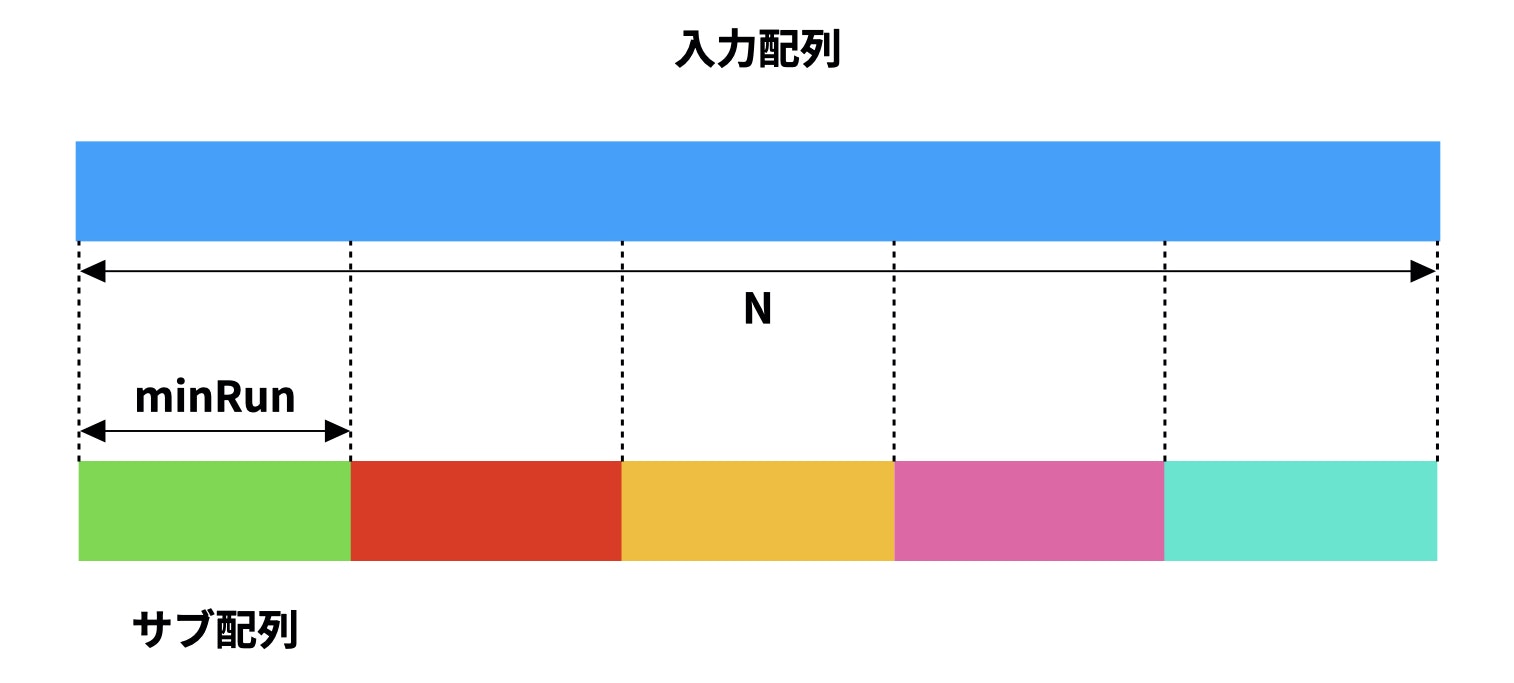
ソートを行う入力配列を、サブ配列と呼ばれる配列に分割します。
そのサブ配列の最低要素数をminRunと呼び、これを計算します。
minRunの値には、次の3条件があります。
- 入力配列の要素数
NとminRunについて、 $\frac{N}{minRun}$ が2の累乗(2, 4, 8, 16,...)か、それに近い値であること minRunの値は大きすぎないこと( $minRun < 256$ )minRunの値は小さすぎないこと( $minRun > 8$ )
上記条件を満たし、最も高いパフォーマンスを出せるのは $32 \leqq minRun \leqq 64$ とのことです。
この数値を入力配列の要素数Nから計算するために次のような関数を使用します。
# minRunの計算をする関数
def calcMinRun(n):
r = 0
while n >= 64:
# 最下位ビットが1である場合、r=1になる
r |= n & 1
# nを1桁右シフト(n // 2 みたいなもの)
n >>= 1
return n + r
ぱっと見て難しいですが、要は、Nを2進数で表した時の上位6ビット( $2^6 = 64$ )を除いた、下位ビットに1が一つでもある場合に、rの値が1になります。(rは 0 or 1 です)
上の例1, 2はそれぞれ minRun = 38, minRun = 32 となります。
STEP2. minRunをもとに配列を分割
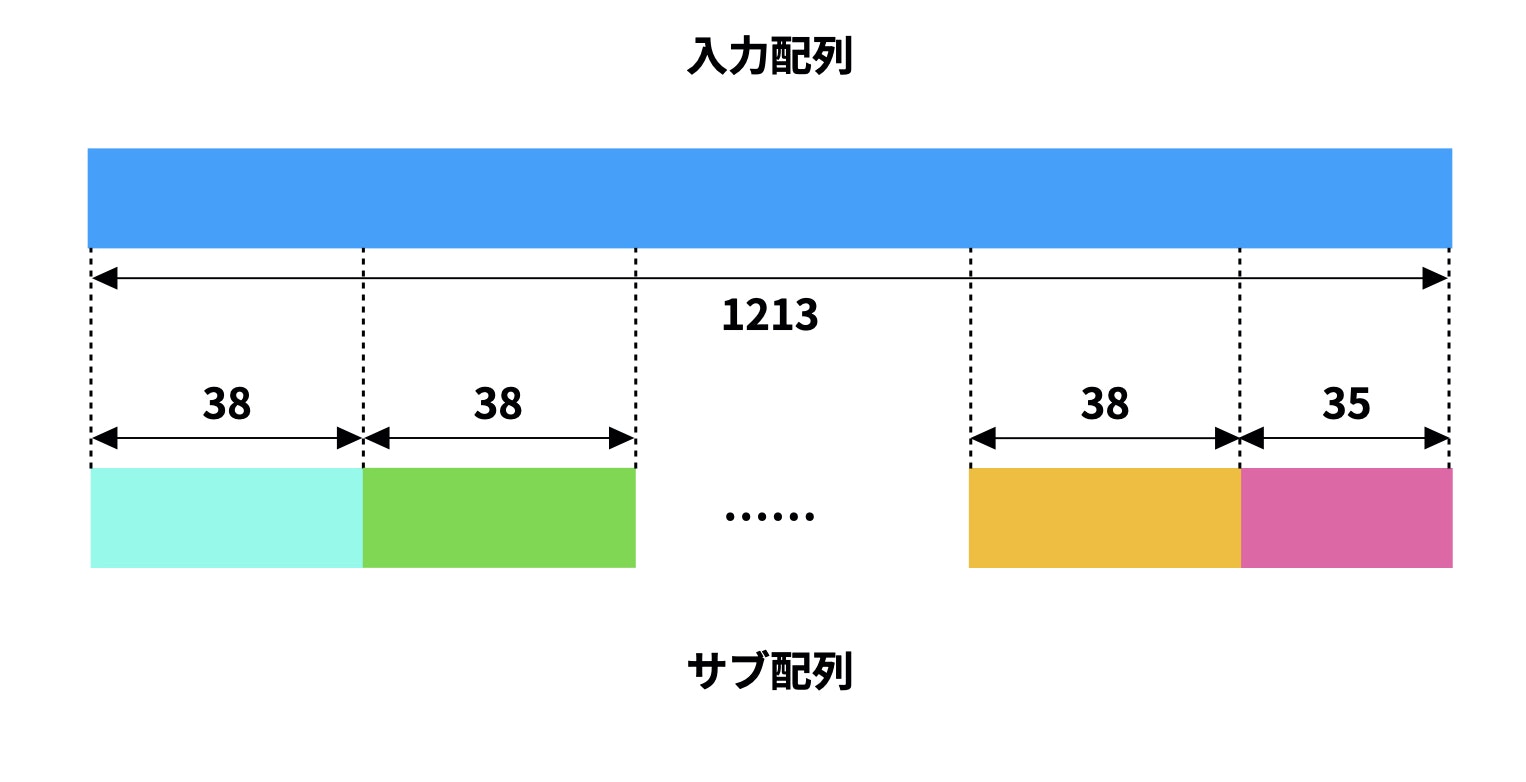
入力配列1をminRunの要素数ずつにスライスし、サブ配列とします。
STEP1の例1だと、次のようになります。
最後のサブ配列がminRunよりも小さくなることがありますが、(本記事では)そのままで扱います。
(後述の「実際のTimsortはもっとすごい」にて少し説明を加えます。)
なお、 $\frac{N}{minRun} = 31.921...$ となっており、 $2^5 = 32$ に近い値であることがわかります。
3. 分割した配列ごとに挿入ソートを実施
分割したサブ配列全てに対して挿入ソートを行います。本記事では、普通の挿入ソートのプログラムを使用します。
挿入ソートの関数
# 挿入ソートを実施する関数
def insertionSort(arr, l, r):
for i in range(l+1, r+1):
j = i
while j > l and arr[j] < arr[j-1]:
arr[j], arr[j-1] = arr[j-1], arr[j]
j -= 1
それでは、ここまでのステップの内容を実際にプログラムで見てみましょう!
# Timsortを実施する関数
def timSort(arr):
# リストの長さを取得
n = len(arr)
# 【STEP1】長さをもとにminRunを計算
minRun = calcMinRun(n)
# 【STEP2】サブ配列に分割(minRunの長さごとに繰り返し実行)
for start in range(0, n, minRun):
# 最終サブ配列時にリストの範囲外アクセスを防ぐ
end = min(start + minRun - 1, n - 1)
# 【STEP3】サブ配列内で挿入ソート実施
insertionSort(arr, start, end)
:
# 【STEP4】分割したソート済み配列にマージソートを実施
:
4. 分割したソート済み配列にマージソートを実施
マージについては、一般的なマージソートの手順と同じです。
既に分割済みのため、マージ作業だけで十分なのです!イメージはこんな感じです。
マージソートの関数(マージのみ)
# マージソート(分割は未実施)を実施する関数
def mergeSort(arr, l, m, r):
left, right = arr[l:m+1], arr[m+1:r+1]
for i in range(l, r+1):
if len(left) == 0:
arr[i] = right.pop(0)
elif len(right) == 0:
arr[i] = left.pop(0)
elif left[0] <= right[0]:
arr[i] = left.pop(0)
else:
arr[i] = right.pop(0)
先程のプログラムの続きを見ていきましょう!
def timSort(arr):
# 【STEP1】長さをもとにminRunを計算
:
# 【STEP2】サブ配列に分割(minRunの長さごとに繰り返し実行)
:
# 【STEP3】サブ配列内で挿入ソート実施
insertionSort(arr, start, end)
# 変数size(マージされたサブ配列の要素数合計をカウント)を用意
size = minRun
while size < n:
# マージする2つのサブ配列の左端のインデックスを取得
for left in range(0, n, 2 * size):
# マージする2つのサブ配列の中央のインデックスを取得
mid = min(n - 1, left + size - 1)
# マージする2つのサブ配列の右端インデックスを取得
right = min((left + 2 * size - 1), (n - 1))
# マージソート実施
mergeSort(arr, left, mid, right)
size = 2 * size
以上が、PythonによるTimsortのシンプル実装となります。
Timちゃん、シンプル実装でも複雑で難しいですね...(泣)