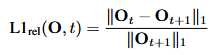HunyuanVideoやWan2.1において高速化する技術としてTeaCacheが実装されている。これについて調べてみる。
ただ、調べるにつれて、これ大した技術じゃなくないか?と個人的には思ってしまったため、やや批判的にまとめている事を御了承ください。
TeaCacheの図
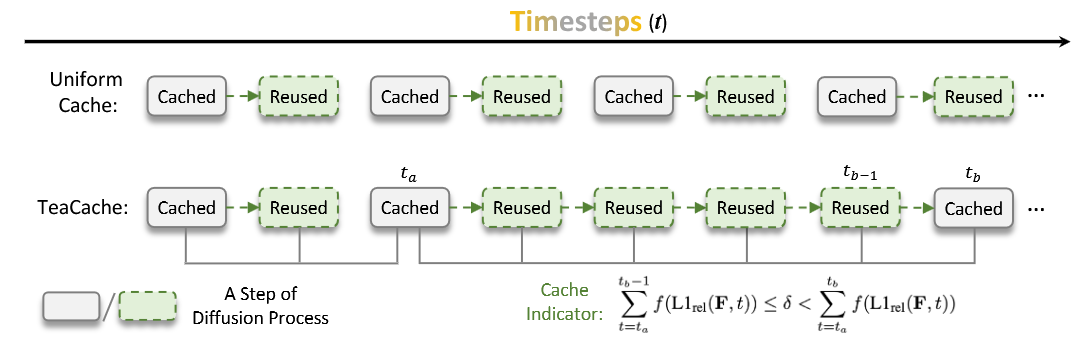
さて、上記のこの図を見ればTeaCacheの概要が理解できる。
要するにTeaCacheとは推論stepの内で変化の少ない推論stepをskipする機能に等しい。
仮に2回に1回、等間隔に推論stepをskipするならばこれは推論stepを単純に半分にする事に等しい。しかし、TeaCacheは非等間隔に推論stepをskipすることが可能である。
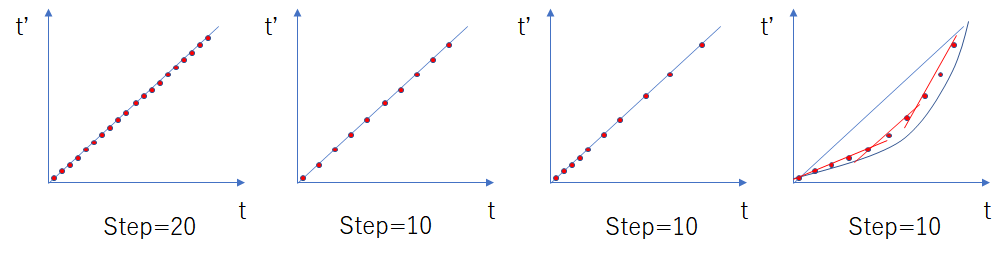
例えば20stepを10stepに削減する事を考えた時、均等に抜いていく場合は下記図において二番目の図の通りである。これは単に推論stepを減らすのに等しい。
一方、前半はあまり間引かず後半に間引く数を増やしていく場合(三番目の図)、この点を再度等間隔に並び替えればこれはHunyuanVideoのshift関数に近い。要するにshift関数が推論stepを少なくして精度が維持できるのと同じようにTeaCacheも変化のほとんどない推論stepを省略して推論回数(latentをDiTに通す回数)自体を減らせるのである。
推論step毎に変化を測定すれば、それが今回stepにおいて小さい場合は次のstepでも変化が小さい事を期待できる。例えば閾値を$\delta=0.25$と設定した時、変化が$L1=0.04$ならその後の5stepをskip出来る。変化が$L1=0.05$ならその後の4stepをskip出来る。$L1=0.10$であれば次の1stepをskip出来る。実際にはtimestepが線形でない場合はこのようなL1は線形増加するわけではないからもっと複雑であろうが、このようにL1を計算していって、その合計値がある値を超えるまではskip出来るという算段なのだろう。
議論:
以下自分が疑問に思った項目を上げる。
推論1回目をCacheして、2回目を高速化する?
「TeaCache 2回目」で検索するとそういう理解をしていた人もいた。
自分も最初そうなのかと思ったのだが、コードを読んだ限りでは同一推論内の変化が小さい場合にskipが有効であり、前回推論(前の動画)の結果を再利用している訳ではないように思った。これについてはおそらくtorch.compileと混同してるのではないか(TeaCacheコード内にtorch.compileがある)。
何故推論stepのskipと表現しないのか?
論文中にはskipという表現はなくCacheという表現を用いている。しかし、個人的にはこの表現は分かりにくいと思った。この推論stepによるずれを再利用する(reused)というよりはskip_step分を一気に進んでしまうように見えるため、Cacheという説明は誤解を招くように思う。
おそらくは過去の論文においてCacheを用いているからなのだろうが、これは読んでない。
PositivePromptとNegativePromptの独立性
たとえばある推論stepにおいてPositivePromptの推論はskipせずに、NegativePromptの推論はskipするみたいな事を考えてないのかと思ったのだが、論文の図や数式を見る限りこのような変化はない。
しかし、TeaCacheのlogにおいて以下のような場合があり、cond(Positive)とuncond(Negative)のskip数が異なる事はあるようだ。これはどうやっているのだろう?
TeaCache skipped:
34 cond steps
33 uncond step
out of 50 steps
実際cfgとこのTimestepの線形補間の合わさった議論は複雑で
cfgの移動は
$x_{t+1,cfg}=\epsilon(x_t,uc)+cfg(\epsilon(x_t,c)-\epsilon(x_t,uc))=\epsilon(x_t,c)+(cfg-1)\cdot (\epsilon(x_t,c)-\epsilon(x_t,uc))$
Timestepの線形移動は通常のモデルだとDiTを通してもt方向には$\frac{1}{1000}$しか動かないから$t_n=1~1000$、$\Delta t=(t_{n+1}-t_n)$として
$x_{t+1,timestep}=x_t+\Delta t(\epsilon(x_t,c)-x_t)=\epsilon(x_t,c)+(\Delta t-1)(\epsilon(x_t,c)-x_t)$
だからPositivePromptとNegativePromptを同時にskipするなら
$x_{t+2}=\epsilon(x_t,c)+2(\Delta t-1)(\epsilon(x_t,c)-x_t)+2(cfg-1)\cdot (\epsilon(x_t,c)-\epsilon(x_t,uc))$
てな感じだが、仮に2回目のPositivePromptの推論はskipせずに、NegativePromptの推論はskipする場合、どのような線形近似によって示せるか。以下、適当に書いたが微妙。
$\epsilon(x_{t+1},uc)≒\epsilon(x_{t},uc)+(cfg-1)\cdot (\epsilon(x_t,c)-\epsilon(x_t,uc))+\Delta t(\epsilon(x_t,c)-x_t)$
$x_{t+2}=\epsilon(x_{t+1},c)+(\Delta t-1)(\epsilon(x_{t+1},c)-x_{t+1})+(cfg-1)(\epsilon(x_{t+1},c)-\epsilon(x_{t+1},uc))$
ここで近似値である$\epsilon(x_{t+1},uc)$を代入する。
推論stepの余剰性
結局TeaCaheが推論stepを削減できるかどうかは推論stepに無駄な推論stepがどのくらい含まれているかによる。つまり、TeaCaheの削減率は推論stepの多さに依存するはずである。
論文の図でも推論stepが50とか150とか多いとより多く削れる。しかし、仮にHunyuanvideoで推論stepをギリギリまで削っている場合は、削減効果は小さいか性能劣化が大きい事になる。
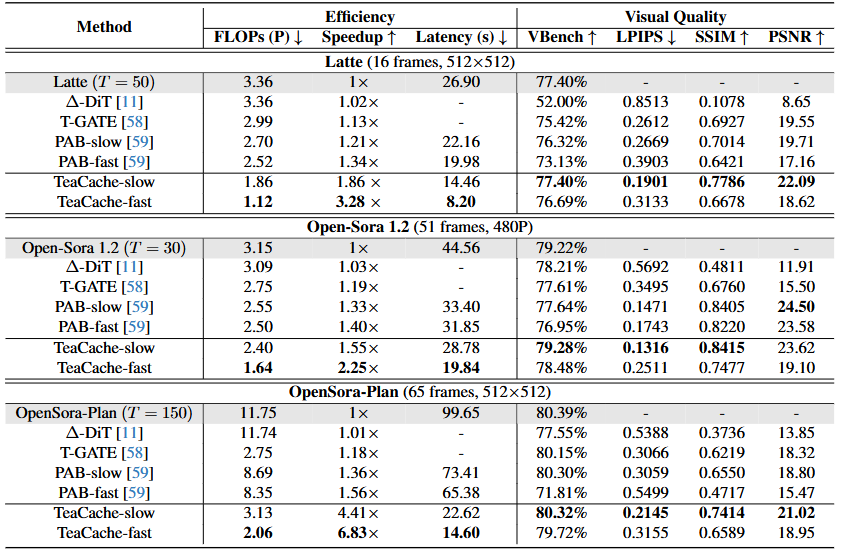
例えば以下においては確かにTeaCacheによって推論を2倍高速化してるように見えるが、推論stepがt2vにおいては「50step」なので元から25stepで推論可能であるなら実質高速化してないことになる。
# The default sampling steps are 40 for image-to-video tasks and 50 for text-to-video tasks.
if args.sample_steps is None:
args.sample_steps = 40 if "i2v" in args.task else 50
また、以下のワークフローではTeaCacheで1.6倍に高速化すると主張しているがstepが30なので18step程度にしかなっていない。その程度で有ればshift値を大きくすればstepを下げても品質はそれ程下がらず描ける。
理想的なshift関数との対比
shift関数の考え方はTeaCacheなどの考え方と推論stepを削減できる結果的な意味である程度近いように思う。無論、HunyuanVideoのshift関数以外にもMovieGenではまた違ったshift関数を定義しているため、理想的なShift関数と乖離があり、まだ最適でない可能性はある。
でもそれなら最適なshift関数を見出し、提案できればよいがおそらくそんなものは存在しない。なぜならこの最適なshift値はモデルや生成動画解像度や推論stepやpromptに多分依存するからである。
従ってTeaCacheのある特定の推論環境において独特なshift関数を見出そう(とも解釈できる)姿勢は面白いが、そのためには逆説的にL1を計算する推論stepが十分に大きくなくてはならないのである。推論stepが十分小さければ既に削減余地はまったくない。
性能劣化の危惧
これは個人的な性格に起因するかもしれないが自分は推論stepをギリギリまで切り詰めることに消極的である。例えば仮に推論stepを20stepを18stepでもそれほど性能劣化ないよと仮に他人から言われたとしても、変えようとは思わない。何故ならその人の動画の解像度とかcfgとかshiftとかpromptでそれほど性能劣化なかったとしても自分の環境では分からないからである。
推論stepを単純に小さくすると出来上がる動画は変化する可能性が高い。また、同時にshift値を調整する必要がある。一方、TeaCacheは変化が小さい推論step(厳密にはその次の推論step)をskipするだけだから、出来上がる動画自体には変化は小さいというメリットはある。しかし、生成速度しか見ておらず閾値を調整するのなら、生成速度が速くなっても不良率が上がる可能性があり、元も子もない。
要するにTeaCacheとは推論stepを減らす試みに近いものであり、それが尊い試みとするのか、蛮勇に過ぎないとみるかは意見が分かれるものであろう。
コードを見る
以下でskip_stepを計算している。これは単に前回のstepの値と今回の値の差分のabs.meanをもとめ、これのstep毎の足し合わせがrel_l1_threshを超えるのを探すだけである。
def teacache_hunyuanvideo_forward(
...
else:
self.accumulated_rel_l1_distance += poly1d(coefficients, ((modulated_inp-self.previous_modulated_input).abs().mean() / self.previous_modulated_input.abs().mean()))
if self.accumulated_rel_l1_distance < rel_l1_thresh:
should_calc = False
self.skip_steps += 1
else:
should_calc = True
self.accumulated_rel_l1_distance = 0
self.skip_steps = 0
self.previous_modulated_input = modulated_inp
このself.skip_stepが使われるコードの一例を示すが、上記の値を代入すれば推論stepをskip出来るのだろう。
class ModelSamplingDiscreteDistilled(comfy.model_sampling.ModelSamplingDiscrete):
original_timesteps = 50
def __init__(self, model_config=None, zsnr=None):
super().__init__(model_config, zsnr=zsnr)
self.skip_steps = self.num_timesteps // self.original_timesteps
sigmas_valid = torch.zeros((self.original_timesteps), dtype=torch.float32)
for x in range(self.original_timesteps):
sigmas_valid[self.original_timesteps - 1 - x] = self.sigmas[self.num_timesteps - 1 - x * self.skip_steps]
self.set_sigmas(sigmas_valid)
def timestep(self, sigma):
log_sigma = sigma.log()
dists = log_sigma.to(self.log_sigmas.device) - self.log_sigmas[:, None]
return (dists.abs().argmin(dim=0).view(sigma.shape) * self.skip_steps + (self.skip_steps - 1)).to(sigma.device)
def sigma(self, timestep):
t = torch.clamp(((timestep.float().to(self.log_sigmas.device) - (self.skip_steps - 1)) / self.skip_steps).float(), min=0, max=(len(self.sigmas) - 1))
low_idx = t.floor().long()
high_idx = t.ceil().long()
w = t.frac()
log_sigma = (1 - w) * self.log_sigmas[low_idx] + w * self.log_sigmas[high_idx]
return log_sigma.exp().to(timestep.device)
まとめ
TeaCacheについて調べた。
TeaCacheは雑に推論stepの大きい環境であればこれは良く働くだろうが、実際には既にshift関数によってある程度効率よく推論stepを減らしてくれている筈なので、自分はこれについて懐疑的に思った。