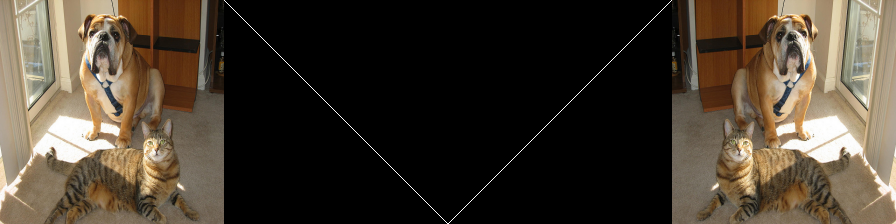
畳み込みは一般に平行移動に強く、画像が任意量だけ平行移動した際でも畳み込みによって元の画像と同じようにその特徴量を取り出すことが出来る、という事は有名である。
一方、畳み込みは拡大・縮小や回転に対しては万能ではなく、同じ畳み込み重みでは拡大した画像や回転した画像からは同じ特徴量を得る事が出来ない。拡大・縮小や回転した画像にはそのサイズや角度に適した別の畳み込み重みを考える必要がある。
厳密にはData Augmentationではないのだが、モデル内である計算を行う事で画像を任意サイズに拡大・縮小を行う全結合を考えてみたい。
モデル
入力を$(H,W,C)=(224,224,3)$、出力を$(224,224,3)$とする。
$H$方向の全結合重み$H_{in}×H_{out}=(224,224)$
$W$方向の全結合重み$W_{in}×W_{out}=(224,224)$を定義する。
行列の並びを入れ替えつつ$(224,224)$の重みを持つ全結合を二回行う。
from tensorflow.keras import Input
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Dense, Permute
input = Input(shape=(224, 224, 3))
x = Permute((2,3,1))(input)
x = Dense(224, use_bias=False)(x)
x = Permute((2,3,1))(x)
x = Dense(224, use_bias=False)(x)
y = Permute((2,3,1))(x)
model = Model(input, y)
model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 224, 224, 3)] 0
_________________________________________________________________
permute (Permute) (None, 224, 3, 224) 0
_________________________________________________________________
dense (Dense) (None, 224, 3, 224) 50176
_________________________________________________________________
permute_1 (Permute) (None, 3, 224, 224) 0
_________________________________________________________________
dense_1 (Dense) (None, 3, 224, 224) 50176
_________________________________________________________________
permute_2 (Permute) (None, 224, 224, 3) 0
=================================================================
Total params: 100,352
Trainable params: 100,352
Non-trainable params: 0
_________________________________________________________________
恒等変換
モデルの二回の全結合重みに対角行列を与える。
重みは255倍してPIL画像にする。この場合、入力画像とモデルの出力画像は等しい。
import numpy as np
from PIL import Image
model_weight1 = np.eye(224)
model_weight2 = np.eye(224)
model_weight1_img = Image.fromarray((model_weight1*255).astype(np.uint8))
model_weight2_img = Image.fromarray((model_weight2*255).astype(np.uint8))
model.layers[2].set_weights([model_weight1])
model.layers[4].set_weights([model_weight2])
...
img = Image.open('cat_dog.png')
img2 = np.asarray(img)
img2 = img2.reshape([1,224,224,3])
img3 = model.predict(img2)[0]
img3 = Image.fromarray(img3.astype(np.uint8))
img4 = get_concat_h_multi_blank([img,model_weight1_img,model_weight2_img,img3])
img4.show()
垂直反転・水平反転
対角行列の並びを反転させると画像が反転する。
一回目の全結合重みを反転させると垂直反転で二回目の全結合重みを反転させると水平反転になる。
flip_vertical = True
flip_horizontal = False
if flip_vertical:
model_weight1 = model_weight1[:,::-1]
if flip_horizontal:
model_weight2 = model_weight2[:,::-1]
拡大・縮小
全結合重みを画像化して横幅を拡大してからクロップする。
この画像を全結合重みに変換して設定する。何故か一部のデータが欠損するが、理由は分からない。例えば、犬の足元の左側の床が黒くなってる。
def crop_center(pil_img, crop_width, crop_height):
img_width, img_height = pil_img.size
return pil_img.crop(((img_width - crop_width) // 2,
(img_height - crop_height) // 2,
(img_width + crop_width) // 2,
(img_height + crop_height) // 2))
x_scale = 0.5
y_scale = 0.7
model_weight1 = np.eye(224)
model_weight2 = np.eye(224)
model_weight1_img = Image.fromarray((model_weight1*255).astype(np.uint8))
model_weight2_img = Image.fromarray((model_weight2*255).astype(np.uint8))
model_weight1_img = model_weight1_img.resize((int(224*y_scale), 224), Image.BILINEAR)
model_weight2_img = model_weight2_img.resize((int(224*x_scale), 224), Image.BILINEAR)
model_weight1_img = crop_center(model_weight1_img, 224, 224)
model_weight2_img = crop_center(model_weight2_img, 224, 224)
model_weight1 = np.asarray(model_weight1_img)/255.0
model_weight2 = np.asarray(model_weight2_img)/255.0
model.layers[2].set_weights([model_weight1])
model.layers[4].set_weights([model_weight2])
x_scale = 1.2
y_scale = 1.5
複数の縮小を並べる
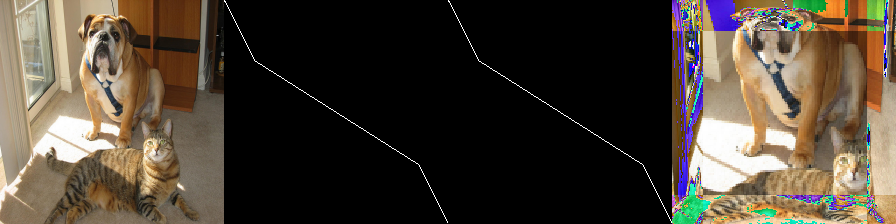
縮小の全結合重みを横に並べて結合すると複数の縮小画像を結合した結果が得られる。縦に三通りの傾きの線が通っているが、三本目の線は非常に薄くて目を凝らさないと見えない。
この結果は重みの平行移動が画像の平行移動にもなっていることを示唆する。
def get_concat_h_blank(im1, im2, color=(0, 0, 0)):
dst = Image.new('RGB', (im1.width + im2.width, max(im1.height, im2.height)), color)
dst.paste(im1, (0, 0))
dst.paste(im2, (im1.width, 0))
return dst
def get_concat_h_multi_blank(im_list):
_im = im_list.pop(0)
for im in im_list:
_im = get_concat_h_blank(_im, im)
return _im
model_weight1_img_a = model_weight1_img.resize((int(224*0.6), 224), Image.BILINEAR)
model_weight1_img_b = model_weight1_img.resize((int(224*0.3), 224), Image.BILINEAR)
model_weight1_img_c = model_weight1_img.resize((int(224*0.1), 224), Image.BILINEAR)
model_weight2_img_a = model_weight2_img.resize((int(224*0.6), 224), Image.BILINEAR)
model_weight2_img_b = model_weight2_img.resize((int(224*0.3), 224), Image.BILINEAR)
model_weight2_img_c = model_weight2_img.resize((int(224*0.1), 224), Image.BILINEAR)
model_weight1_img = get_concat_h_multi_blank([model_weight1_img_a, model_weight1_img_b, model_weight1_img_c])
model_weight2_img = get_concat_h_multi_blank([model_weight2_img_a, model_weight2_img_b, model_weight2_img_c])
model_weight1_img = crop_center(model_weight1_img, 224, 224)
model_weight2_img = crop_center(model_weight2_img, 224, 224)
model_weight1 = np.asarray(model_weight1_img)[:,:,0]/255.0
model_weight2 = np.asarray(model_weight2_img)[:,:,0]/255.0
Cutout
Data Augmentationで画像の任意領域を黒塗りにする操作をCutoutという。
$x,y$の任意領域をそれぞれ黒塗りにする事は可能だが、両方使うと得られる黒く塗り領域はCutoutのような長方形状ではなく十字領域になる。
model_weight1[150:200,150:200] = 0
model_weight2[50:70,50:70] = 0

また、逆のことをやれば、ある任意範囲のみの画像を領域を取り出すこともできる。
元の画像からこの領域を差し引くことでCutoutに相当する任意領域を黒塗りは作成できる。
model_weight1[:150,:150] = 0
model_weight1[200:,200:] = 0
model_weight2[:50,:50] = 0
model_weight2[120:,120:] = 0
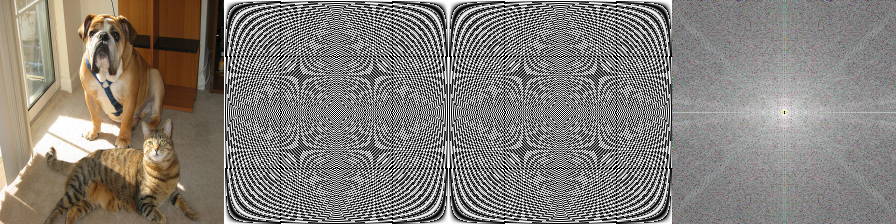
対角行列がS字の直線
対角行列がカーブする時
離散フーリエ変換(DFT)
W_N^n=e^{-2\pi i(n/N)}

全結合重みが上記の様な係数を与える行列ならこの全結合演算は$H$または$W$の離散フーリエ変換(DFT)に等しいと見なせる(…筈である)。
model_weight1 = np.zeros((224,224))
model_weight2 = np.zeros((224,224))
for i in range(224):
for j in range(224):
model_weight1[i,j] = np.exp(-2*np.pi*1j*i*j/224)
model_weight2[i,j] = np.exp(-2*np.pi*1j*i*j/224)
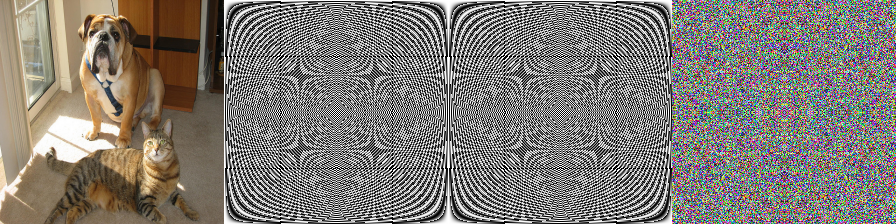
画像の2次元FFTでよく知る中心に十字の放射状の周波数スペクトルに似てないが、あっちは複素数の絶対値の結果にlogを掛ける強度スペクトルであるからだろう。虚部のモデルも作成すれば以下の様に良く知る周波数スペクトルが得られる。
img3a = model.predict(img2)[0]
img3b = model2.predict(img2)[0]
img3 = img3a + 1j * img3b
img3 = np.fft.fftshift(img3)
img3 = 20 * np.log(np.absolute(img3))
ここでDFTの計算量は$O(N^2)=224224(行列積の負荷)$。
一方、FFTは$O(Nlog_2N)$で$2^8=256$で$8$回のバタフライ演算をする事で良く、物理的な計算量が$8*(バタフライ演算)=2568((行列積の負荷+ビットリバースの負荷))$で済む。十分に$N$が大きければ当然FFTは速度的に有利だが、ビットリバースの負荷が無視できない$N$の大きさでは必ずしもFFTはDFTより速くならないはずである。
クロネッカーのデルタ関数
恒等変換に掛けている対角行列がクロネッカーのデルタと同じで以下の定義がある。
\delta_{i,j}=\begin{cases}
1 & ( i = j ) \\
0 & ( i \neq j )
\end{cases}
さて、ここでクロネッカーのデルタを示す関数を$relu$関数を用いて表現してみたい。
f(i,j)=relu(1+(i-j)-2\cdot relu(i-j))
と定義すればこれはクロネッカーのデルタである事が分かる。
f(i,j)=\begin{cases}
relu(1-(i-j))=0 & ( i -j \geqq 1 ) \\
1 & ( i -j = 0 )\\
relu(1+(i-j))=0 & ( i -j \leqq -1 )
\end{cases}
ここでpos_embである$r=(1,2,3...,224)$を与え、$f(r_i,r_j^T)\cdot x$の行列演算を考えれば、これは対角行列を掛ける全結合(恒等変換)に等しい。
ここで$(i-j)→(2i-j)$とすれば傾き1以外の対角行列も作れる。
90°回転
$(H,W,C)$の行列を$(W,H,C)$の行列に軸順番を操作を追加するとy = Permute((2,1,3))(x)、結果を90°回転することが出来る。
一方でこれまでの$H×H$全結合の重みや$W×W$の全結合をいくら考えても回転操作を与える全結合重みは与える事が出来ない。
input = Input(shape=(224, 224, 3))
x = Permute((2,3,1))(input)
x = Dense(224, use_bias=False)(x)
x = Permute((2,3,1))(x)
x = Dense(224, use_bias=False)(x)
x = Permute((2,3,1))(x)
y = Permute((2,1,3))(x) # 追加。HとWを入れ替え
model = Model(input, y)
任意角回転
これは次元を結合して$HW×HW$の全結合重みを与えれば任意角回転に相当する全結合重みを得ることは出来る。しかし、一般に画像サイズが$(224,224)$なら$224\cdot 224 \cdot 224 \cdot224=2.5×10^9$でFP32なら全結合のパラメータに$10GB$のメモリが必要になる。これはあまり現実的ではない。
正直、回転を与える変換がどんな形になるかよく分からない。
MLP-Mixerにおける全結合
画像が$(H,W,C)$で与えらた時、パッチ分割を行うと$(HW/p^2,C\cdot p^2)$という次元になり、
MLP-Mixerではパッチ方向の全結合が$(HW/p^2,HW/p^2)$、チャンネル方向の全結合が$(C\cdot p^2,C\cdot p^2)$である。パッチ方向の全結合は上で議論してきた$H×H$全結合の重みや$W×W$の全結合重みと性質は異なる。むしろ、任意角回転において議論した$HW×HW$の全結合重みに近い。
今回のことを試した動機としてViTのAttentionが入力に依存する任意の画像変換になってたりしないかという事があったのだが、今回のテストはこの疑問の答えには繋がらなかった。
まとめ
畳み込みを行う前に$H×H$全結合の重みや$W×W$の全結合重みを与えた時、その処理は拡大・縮小などの一部のDataAugmentation処理の内容に等しいのではと思った。ただし、今回のように任意の初期全結合重みを与えた場合、その変換は確率的に変化せず、また全ての入力に対し同じ変換しか与えれないためDataAugmentation処理を代替することは出来ない。
利点として挙げられるのは複数の異なるタイプの画像変換が組み合わさった場合(反転、拡大、平行移動)でも、最適化したまとめた全結合重みを作れれば計算は1回で済む(affine変換のように)。
Kerasでのデータ拡張のImageDataGeneratorは今回のように変換をつくる前処理モデルを作って本モデル前に繋げているのだろうか?自前のDataGeneratorの作り方を見る限りはかなり自由に作れるのでそんな感じではないが…。