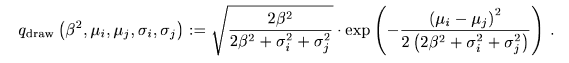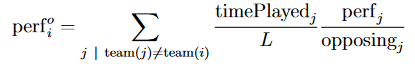前回イロレーティングに対して調べて少し考察した記事を書いた。
ガウス分布であれば複数の分布ばらつきは足してひとつのばらつきに換算できる一方、ロジスティック分布(累積分布がシグモイド関数)では複数の分布のばらつきの足し合わせが困難で一個のばらつきに換算できない。
そもそもイロレーティングにおいては勝敗判定というひとつのばらつきしか定義できない。たとえばプレイヤーAのばらつきとプレイヤーBのばらつきが異なる場合を上手く考慮できない。
このような問題に対してイロレーティングを改善したレーティング方法にMicrosoftのTrueskillがある。これについて調べて考えてみたことを述べたい。
また、グリコレーティングというのもあるらしいがこれについては述べない。
イロレーティング考察続き
イロレート論文
収束に対する議論
たとえばイロレーティングではレーティング差400の場合、勝率は91%である。
要するにプレイヤーA、Bがレート400差で11戦やったら平均10勝1敗となる。
この場合、プレイヤーA、Bのレート差が400差から変わらないためにはプレイヤーAが勝った時の変動量をx1、プレイヤーBが勝った時の変動量をx2と置くなら、強いプレイヤーAが勝った時の変動量x1は僅かで、弱いプレイヤーが勝った時の変動量は大きくする。
10*x_1-1*x_2=0
x_2=10*x_1
例えば仮にAがBに対しレート差400あって$K=32$とすると、Aが勝った場合$+3$、Aが負けた場合$-30$(ここで移動量の比率が重要であり、大きさはそれほど重要ではない)レートが移動し、Aの勝率91%、つまり平均10勝1敗の戦いをする。この場合、変動するレートの期待値はゼロである。$(+3)\cdot10+(-30)\cdot1=0$
仮に二者間の勝率が94%ならレーティング差は400より大きくなり、そこでいずれ安定する。
仮に二者間の勝率が87%ならレーティング差は400より小さくなり、そこでいずれ安定する。
二者間でレート移動していればいずれ全体で平衡に達する。
問題にしたいのは勝率が100%に近づくにつれ正確な勝率を見分けるのが困難になるのではという事である。91%と94%を見分けるには相当数の対戦をやらないと正確にはならない。中央付近のレートに比べて端のレートは収束までに時間が掛かるという事である。
ゼロサムゲーム
イロレーティングで勝った時と負けた時でレートの変動量が違う事で勘違いしそうになるが基本的にはこのレートは勝者が得るレートと敗者が失うレートが等しいゼロサムゲームである。
だからみんなが勉強して全員が偏差値60を超える事がないように、全員が平均以上になることはあり得ないし、そうなるとしたらレーティングインフレが発生していることになる。
インフレ、デフレはゲームの極端に高いスコアまたは低いスコアの引退者がでると発生する。ゼロサムゲームによりプレイ環境のレート平均が引退者分だけ増えるか減る。
そのようなインフレ、デフレの場合、補正するには全員のスコアを等しく減らす/増やすだけでプレイヤー間のレート差を変えず、全プレイヤー平均値を容易に補正できると思うのだが、何故かその補正の記述はwiki内で見なかった。むしろ、インフレ、デフレの問題を解決困難な深刻な問題かのように記述している。
チェスなどではイロレート下限を2200と設定しているため衰えた引退者が負債を背負って引退することで環境内の数値インフレが起こっているらしいが、純粋なイロレーティングでは引退者の補正は容易でこのようなインフレは起こらないはずである。
別の意味でのレートインフレ
イロレートにレベルの低い新規プレイヤーを大量に追加すると、既存プレイヤーのレートは相対的に上昇する。この現象もイロレーティングのインフレと呼べる。
レートのインフレを意図的に起こすには平均レートより低い新規プレイヤーをレート内に参入させて平均レートプレイヤーのレベルを下げて、相対的にレートを上げる。または上位プレイヤーを別のレートに隔離する。これを継続的に起こすためには新規プレイヤーの平均レベルを徐々に落とすと良い。または上位プレイヤーを隔離するレベルを徐々に下げればよい。
仮に二個の上位レートと下位レートが採用されているゲームの場合、緩やかにこの二個のレートの境界の閾値を下げると下位レートでも上位レートでも平均レートプレイヤーのレベルが下がり、両方のレートでレートのインフレが発生する。漸次にレートが上昇する方がプレイヤーとしては楽しいのではないか。
一方でこのようにインフレを起こすとたくさんのお金がもらえてお金持ちになったような錯覚を起こすが実際に持ってる資産の価値は変化ない。また、あまりに閾値を下げすぎると上位レートに昇格した価値自体が棄損されたという不満が出るだろう。
とはいえ別にこれらは一般的なレートやランクでもそうでイロレーティング特有の事象ではない。
レート分布と偏差値換算
イロレーティングのレート分布は勝利確率がシグモイド関数なのでプレイヤーの分布はロジスティック分布になると思われる。
英語wikiの記述によれば正規分布の分散では200に$10/7$を掛けた値でこれが$200*\sqrt{2}$の近似であるという導出がある。これは勝利確率が正規分布に由来するとする場合はよい。
一方で、勝利確率がロジスティック分布に由来するとする時、これはシグモイド関数の係数である$log(10)$とロジスティック分布の分散である$\pi^{2}/3$が現れていない。
これを計算すると以下の様な係数となるため、ちょうど$10/7$の近似値が現れる。
$\log(10)*\frac{3}{\pi^2}=0.69990194...$である。
イロレーティングの底$10$は$\sqrt{2}/2=0.70710678..$の正規分布の累積分布関数をシグモイド関数で近似するのにちょうどいい値$(0.69990194..)$である。そして、このシグモイド関数を真理とおいて逆に正規分布の累積分布関数を近似関数に見なす場合、係数は$0.69990194..≃7/10$となる。
for i in [0,50,100,150,200,250,300,350,400,800]:
a = np.log(10)*3/np.pi**2
x = R0 + i + 400*np.random.randn(point)*a
x2 = R0
x3 = np.mean((1+np.sign(x-x2))/2)
xa = R0 + i
x2a = R0
x3a = np.mean((1+scipy.special.erf(np.sqrt(2)/2*(xa-x2a)/400/a))/2)
x4 = 1/(1+10**(-i/400))
print(i, x3, x3a, x4)
print('a=', a)
-------------------------------------------------
0 0.49906 0.5 0.5
50 0.57134 0.5708727077728624 0.5714631174083814
100 0.639312 0.6395262974318514 0.6400649998028851
150 0.702488 0.7039479252481624 0.7033850034718286
200 0.762912 0.7625056712957201 0.7597469266479578
250 0.814692 0.8140666569764456 0.8083176725494586
300 0.858144 0.8580453437615487 0.8490204427886767
350 0.894772 0.8943822100881913 0.8823382970469413
400 0.923452 0.9234650512422353 0.9090909090909091
800 0.997764 0.9978653271131183 0.9900990099009901
a= 0.6999019411780774
さて、イロレーティングの偏差値換算してみたい。日本人にとっては偏差値の方が卑近かと思った。
$R_0=1500$のばらつき$400$とすれば前述の$7/10$を用いれば以下の様になる。ばらつき400のロジスティック分布は$\sigma=280$のガウス分布で近似できる。偏差値70以上はガウス分布では上位2.28%である。
しかしながら、ロジスティック分布とガウス分布の差はレート差が大きいほどその値にずれが大きい。このため偏差値換算はレートの大きい場所では正確ではないかもしれない。
| 偏差値 | 50 | 55 | 60 | 65 | 70 |
|---|---|---|---|---|---|
| イロレーティング | 1500 | 1640 | 1780 | 1920 | 2060 |
for i in [0,140,280,420,560]:
a = np.log(10)*3/np.pi**2
x = R0 + i + 400*np.random.randn(point)*a
x2 = R0
x3 = np.mean((1+np.sign(x-x2))/2)
xa = R0 + i
x2a = R0
x3a = np.mean((1+scipy.special.erf(np.sqrt(2)/2*(xa-x2a)/400/a))/2)
x4 = 1/(1+10**(-i/400))
print(i, x3, x3a, x4)
print('a=', a)
-------------------------------------------------
0 0.498892 0.5 0.5
140 0.691784 0.6914871236620765 0.691236152414763
280 0.842444 0.8413786446772551 0.8336624691834381
420 0.933484 0.9332200132745672 0.9181681752448481
560 0.976792 0.9772649924770245 0.9617134961177454
a= 0.6999019411780774
ところでグリコレーティングでは$\sigma=350$と中途半端な値になっているが、これは$400*7/10*1500/1200=350$であろう。このため$R_0=1500$でRDは$350$のグリコレーティングに$12/15$を掛けると、$R_0=1200$でばらつき$400$($\sigma=280$)のイロレーティングと一致するだろう。
イロレートは面白いか?精神的な話
よくレートの開始時点が1500のため、よく1500以上の優秀さの指標にするが、まず半分の人間が1500以下であることを無視している。そして1500以下の人間にとってイロレートの向上を目指すモチベは、当然低くなる。何故なら開始時点で1500であるためレートの減少しか経験しないプレイヤーはこのレートが面白くない。しかも、その割合も50%もいる。
初期のレートがある程度安定するまではユーザには非表示にして、安定してから表示させればいいのではと思ったが、この場合は1500からレートを上げていく醍醐味が失われる。
あくまでゲームの楽しさでいえば、どこかで収束するにせよ漸次増加するレートの方が成長を感じられてプレイヤーは楽しいと感じるのではと思った。一方、Trueskillは後述するが新規レート参加者のレートをゼロとするトリックが使用されている。
また、連敗される方の精神に対する検討が不十分ではないだろうか。
普通の人間なら5連敗以上は少しイライラしてパフォーマンスは落ち、実力を発揮できない。おそらく10連敗を超えればその日はゲームを止めるだろう。
連敗中には多少他のプレイヤーに対して不公平でも勝てる相手と戦いたい。
擬似イロレーティング
wikiではイロレーティングを簡略化したレーティングを示されている。
イロレーティングがロジスティック分布であるのに対し、この分布は一様分布であり、この一様分布の累積分布関数は活性関数界隈ではhard_sigmoidとして知られている。
この場合、レート差200で勝率75%、レート差400で勝率100%と勝利確率は線形に推移する。
hard_sigmoidは$W=clip((1+(R_A-R_B)/400)/2,0,1)$で示される。
for i in [0,50,100,150,200,250,300,350,400,800]:
x = R0+i+400*np.random.uniform(low=-1, high=1, size=point)
x2 = R0
x3 = np.mean((1+np.sign(x-x2))/2)
x4 = np.mean(np.clip((1+i/400)/2, 0, 1))
print(i, x3, x4)
-------------------------------------------------
0 0.499152 0.5
50 0.561932 0.5625
100 0.621644 0.625
150 0.687516 0.6875
200 0.749948 0.75
250 0.812672 0.8125
300 0.8742 0.875
350 0.93752 0.9375
400 1.0 1.0
800 1.0 1.0
シグモイド関数の微分
機械学習に通じている人ならシグモイド関数の微分式が$y'=y(1-y)$となるのは有名である。
さて$W_{AB}=sigmoid(a(R_A-R_B))$とした時、$x=a(R_A-R_B)$
\frac{\partial W_{AB}}{\partial R_A}=\frac{\partial W_{AB}}{\partial x}\frac{\partial x}{\partial R_A}=W_{AB}(1-W_{AB})*a
\frac{\partial W_{AB}}{\partial R_B}=\frac{\partial W_{AB}}{\partial x}\frac{\partial x}{\partial R_B}=W_{AB}(1-W_{AB})*(-a)
W_{AB_{new}}=W_{AB}+\frac{\partial W_{AB}}{\partial R_A}\frac{\partial R_A}{\partial t}dt=W_{AB}+(W_{AB}(1-W_{AB})*a)\frac{\partial R_A}{\partial t}dt=W_{AB}(1+W_{BA}*\beta)
R_{new}-R=400\log_{10}\frac{W_{AB_{new}}}{1-W_{AB_{new}}}-400\log_{10}\frac{W_{AB}}{1-W_{AB}}
R_{new}-R=400\log_{10}\frac{W_{AB_{new}}(1-W_{AB})}{(1-W_{AB_{new}})W_{AB}}
ここでリタイヤ。
EloScoreの更新式が非常に簡潔なのはシグモイド関数の微分式が$y'=y(1-y)$と簡単に書ける事が理由ではないかと思った。wikiにあるEloScoreの更新式を勝利確率(シグモイド関数)の微分式から導出を考えてみたが途中でよく分からなくなった。
また、一次の近似ではなく二次の近似でシグモイド関数の二次微分が$y''=y(1-y)(1-2y)$を使って収束があがるのか考えたかった。
f(x_0+dt)=f(x_0)+f'(x_0)dt+\frac{1}{2}f''(x_0)dt^2
ガンベル分布
以下に示すように二個のガンベル分布のばらつきは一個のシグモイド関数に見なせる。
しかしながら、三個以上の分布を足して一個のシグモイド関数にみなすのは困難である。
二個のガンベル分布と判定確率がヘヴィサイドの階段関数はシグモイド関数になる。
for i in [0,50,100,150,200,250,300,350,400,800]:
a = np.log(10)
x = np.random.gumbel(loc=R0+i, scale=400/a, size=point)
x2 = np.random.gumbel(loc=R0, scale=400/a, size=point)
x3 = np.mean((1+np.sign(x-x2))/2)
x4 = 1/(1+10**(-i/400))
print(i, x3, x4)
-------------------------------------------------
0 0.499528 0.5
50 0.573128 0.5714631174083814
100 0.639944 0.6400649998028851
150 0.704072 0.7033850034718286
200 0.760612 0.7597469266479578
250 0.808144 0.8083176725494586
300 0.850128 0.8490204427886767
350 0.883412 0.8823382970469413
400 0.909116 0.9090909090909091
800 0.990032 0.9900990099009901
一個のガンベル分布と判定確率がガンベル分布の累積分布関数はシグモイド関数になる。
for i in [0,50,100,150,200,250,300,350,400,800]:
a = np.log(10)
x = np.random.gumbel(loc=R0+i, scale=400/a, size=point)
x2 = R0
x3 = np.mean(np.exp(-np.exp(-(x-x2)/(400/a))))
x4 = 1/(1+10**(-i/400))
print(i, x3, x4)
-------------------------------------------------
0 0.49919262223011845 0.5
50 0.5717263619417868 0.5714631174083814
100 0.6396198719851675 0.6400649998028851
150 0.7027062365184896 0.7033850034718286
200 0.7598691218278059 0.7597469266479578
250 0.8085584664286181 0.8083176725494586
300 0.849220462344342 0.8490204427886767
350 0.8820465250255853 0.8823382970469413
400 0.9092205928022754 0.9090909090909091
800 0.9900808223949012 0.9900990099009901
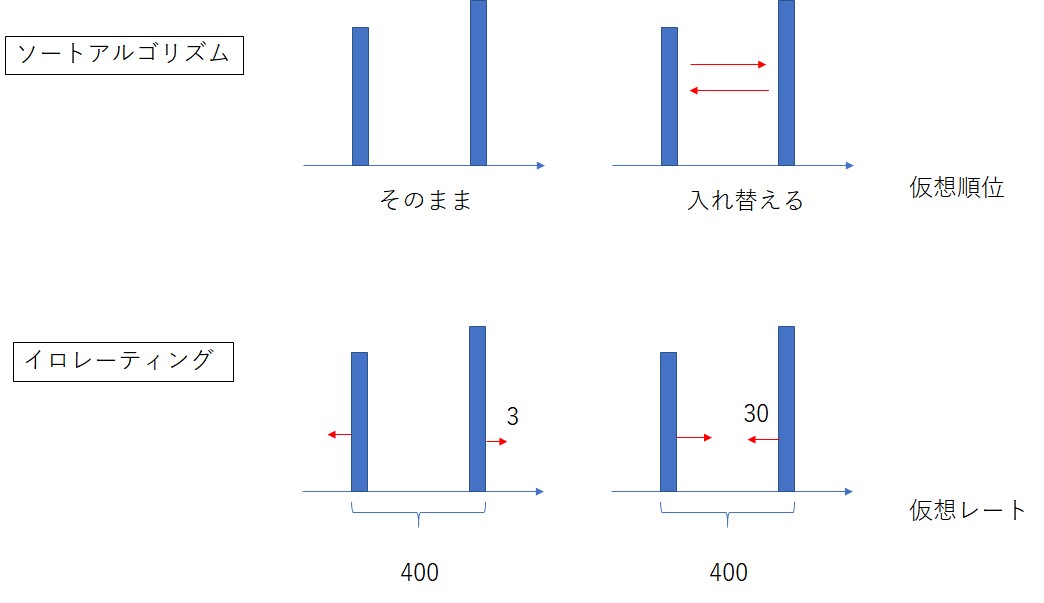
ソートアルゴリズムと計算時間
ソートアルゴリズムとの類似性を考える。
ソートアルゴリズムは交換ソートにおいては二個の値の大小を比較して仮想順位と順番があっていればそのまま、さもなくば入れ替える。
イロレーティングは二個の仮想レートを比較して、仮にレート差が400(勝率91%)、K=32であれば勝ったら$32*0.09$離し、負けたら$32*0.91$縮める。この図を見るとイロレーティングはソートアルゴリズムの一種のように見なせれるのではないかと思った。
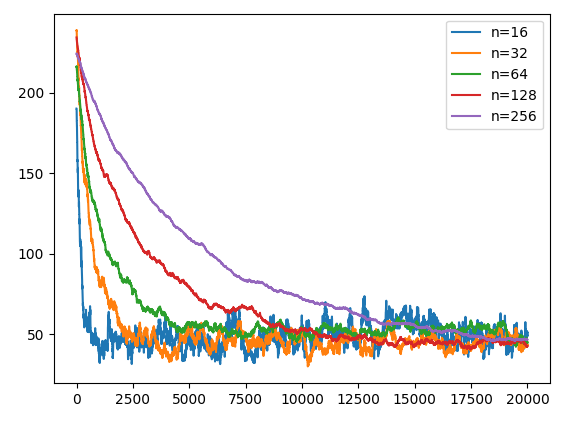
効率のよいソートアルゴリズムなら収束回数は$O(n\log_2n)$になり、簡単なバブルソートとかなら$O(n^2)$となる。$n=2^{10}$なら前者は$10n$であり、後者は$1024n$なので$100$倍違う。イロレーティングの収束回数から計算複雑性理論を考えたい。ただ平均絶対値誤差として一定以下のレート誤差以下を達成するのを目指す。
収束は初期乱数に依存し、nが小さいと見積もりはあまりあてにはならないのだが以下を見ると高々$O(n)$~$O(n\log_2n)$なのではないかと思う。
仮に$n=128$の収束回数を$12800$と仮定すると、収束までの一人当たりのマッチング回数は$200$回といったところだろう。もっとも、分布の中央付近は比較的早く収束するので、分布の端の収束が落ち着くまで中央付近は意味のないマッチングをしている。
import numpy as np
import scipy
import matplotlib.pyplot as plt
import random
K = 32
for n in [16, 32, 64, 128, 256]:
Elo_true = np.random.randn(n) * 400 / np.sqrt(2) + 1500
Elo_pred = np.ones(n) * 1500
l = list(range(n))
loss = []
for t in range(20000):
sample = random.sample(l, 2)
i, j = sample[0], sample[1]
R_AB_true = Elo_true[i] - Elo_true[j]
R_AB_pred = Elo_pred[i] - Elo_pred[j]
W_AB_true = (1+scipy.special.erf(R_AB_true /400))/2
W_AB_pred = (1+scipy.special.erf(R_AB_pred /400))/2
W_BA_pred = 1 - W_AB_pred
if W_AB_true > np.random.rand():
Elo_pred[i] = Elo_pred[i] + K * W_BA_pred
Elo_pred[j] = Elo_pred[j] - K * W_BA_pred
else:
Elo_pred[i] = Elo_pred[i] - K * W_AB_pred
Elo_pred[j] = Elo_pred[j] + K * W_AB_pred
loss.append(np.mean(np.abs(Elo_true-Elo_pred)))
plt.plot(range(len(loss)), loss, label='n=%d'% (n))
plt.legend()
plt.show()
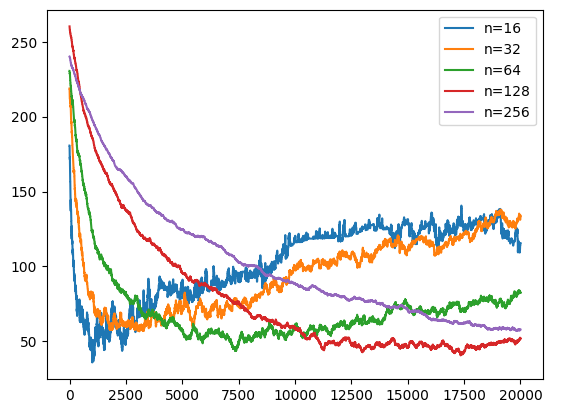
レート差200以上はマッチしないようにする。
仮想レートが$200$以上差のある場合は再マッチする。
マッチング品質は向上するが収束までの回数は特に増えたりも減ったりもしない。
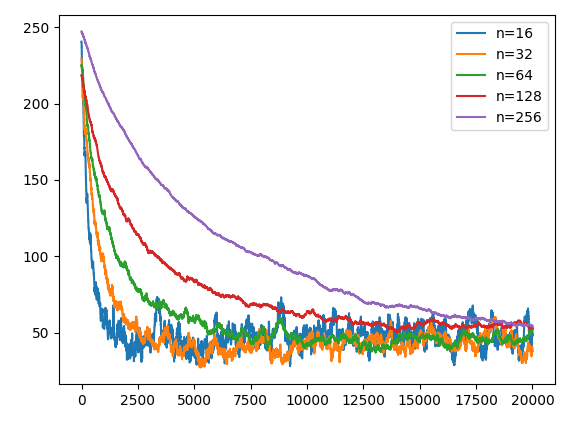
import numpy as np
import scipy
import matplotlib.pyplot as plt
import random
K = 32
for n in [16, 32, 64, 128, 256]:
Elo_true = np.random.randn(n) * 400 / np.sqrt(2) + 1500
Elo_pred = np.ones(n) * 1500
l = list(range(n))
loss = []
for t in range(20000):
for k in range(30):
sample = random.sample(l, 2)
i, j = sample[0], sample[1]
R_AB_true = Elo_true[i] - Elo_true[j]
R_AB_pred = Elo_pred[i] - Elo_pred[j]
if R_AB_pred < 200:
break
W_AB_true = (1+scipy.special.erf(R_AB_true /400))/2
W_AB_pred = (1+scipy.special.erf(R_AB_pred /400))/2
W_BA_pred = 1 - W_AB_pred
if W_AB_true > np.random.rand():
Elo_pred[i] = Elo_pred[i] + K * W_BA_pred
Elo_pred[j] = Elo_pred[j] - K * W_BA_pred
else:
Elo_pred[i] = Elo_pred[i] - K * W_AB_pred
Elo_pred[j] = Elo_pred[j] + K * W_AB_pred
loss.append(np.mean(np.abs(Elo_true-Elo_pred)))
plt.plot(range(len(loss)), loss, label='n=%d'% (n))
plt.legend()
plt.show()
1000回目以降レート差10以下はマッチングしない
プレイヤー数が少ないとレート誤差が増大する。また収束も特に早くならない。
import numpy as np
import scipy
import matplotlib.pyplot as plt
import random
K = 32
for n in [16, 32, 64, 128, 256]:
Elo_true = np.random.randn(n) * 400 / np.sqrt(2) + 1500
Elo_pred = np.ones(n) * 1500
l = list(range(n))
loss = []
for t in range(20000):
for k in range(30):
sample = random.sample(l, 2)
i, j = sample[0], sample[1]
R_AB_true = Elo_true[i] - Elo_true[j]
R_AB_pred = Elo_pred[i] - Elo_pred[j]
if R_AB_pred < 200 and (t>1000 and R_AB_pred>10):
break
W_AB_true = (1+scipy.special.erf(R_AB_true /400))/2
W_AB_pred = (1+scipy.special.erf(R_AB_pred /400))/2
W_BA_pred = 1 - W_AB_pred
if W_AB_true > np.random.rand():
Elo_pred[i] = Elo_pred[i] + K * W_BA_pred
Elo_pred[j] = Elo_pred[j] - K * W_BA_pred
else:
Elo_pred[i] = Elo_pred[i] - K * W_AB_pred
Elo_pred[j] = Elo_pred[j] + K * W_AB_pred
loss.append(np.mean(np.abs(Elo_true-Elo_pred)))
plt.plot(range(len(loss)), loss, label='n=%d'% (n))
plt.legend()
plt.show()
1000回ごとにKの値を半減する
Kの初期値$K=256$として1000マッチごとに$1/2$にする。
$n=128$では早くなったように見えるが、$n=16$では遅くなっている。また$n=256$の収束も十分ではない。$n=16$では$K=256$は大きすぎる。
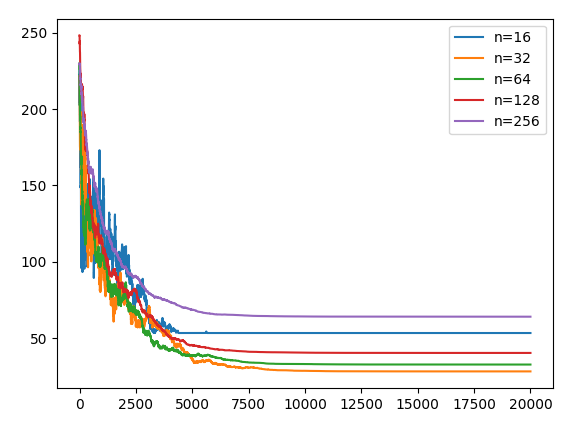
import numpy as np
import scipy
import matplotlib.pyplot as plt
import random
for n in [16, 32, 64, 128, 256]:
Elo_true = np.random.randn(n) * 400 / np.sqrt(2) + 1500
Elo_pred = np.ones(n) * 1500
l = list(range(n))
loss = []
for t in range(20000):
K = 256/2**(t/(1000))
sample = random.sample(l, 2)
i, j = sample[0], sample[1]
R_AB_true = Elo_true[i] - Elo_true[j]
R_AB_pred = Elo_pred[i] - Elo_pred[j]
W_AB_true = (1+scipy.special.erf(R_AB_true /400))/2
W_AB_pred = (1+scipy.special.erf(R_AB_pred /400))/2
W_BA_pred = 1 - W_AB_pred
if W_AB_true > np.random.rand():
Elo_pred[i] = Elo_pred[i] + K * W_BA_pred
Elo_pred[j] = Elo_pred[j] - K * W_BA_pred
else:
Elo_pred[i] = Elo_pred[i] - K * W_AB_pred
Elo_pred[j] = Elo_pred[j] + K * W_AB_pred
loss.append(np.mean(np.abs(Elo_true-Elo_pred)))
plt.plot(range(len(loss)), loss, label='n=%d'% (n))
plt.legend()
plt.show()
これはプレイヤー全体で1000回試合ごとに1/2しているためプレイヤー単体視点ではプレイヤー数によってKの値の半減までの試合数が異なる。
Kの値を動的に変えればもっと収束は早くなるかもしれないがイロレーティングにおいてされていない。一方、TrueskillにおいてこのKの動的変化はされている。
Trueskillについて
Trueskill初期値
Trueskillの初期値は$\mu=25, \sigma=25/3, \beta=25/6,\tau=\sigma/100$である。
import trueskill
mu = 25.
sigma = mu / 3.
beta = sigma / 2.
tau = sigma / 100.
draw_probability = 0.1
backend = None
env = trueskill.TrueSkill(
mu=mu, sigma=sigma, beta=beta, tau=tau,
draw_probability=draw_probability, backend=backend)
Trueskillとイロレーティングの互換性
イロレーティングの互換性を考えると$\mu=1200, \sigma=400, \beta=200,\tau=\sigma/100$とするのが良いと思う。
例えば、以下の様に記述した場合、勝利確率がシグモイド関数であるイロレーティングとばらつきは一致する。またTrueSkillの勝利確率は係数$\sqrt{2}/2$の正規分布の累積分布関数に一致しているのが確認できる。一方、シグモイド関数とは若干違う。
import trueskill
import numpy as np
import scipy
import itertools
import math
mu = 1200
sigma = mu / 3.
beta = sigma / 2.
tau = sigma / 100.
draw_probability = 0.1
backend = None
env = trueskill.TrueSkill(
mu=mu, sigma=sigma, beta=beta, tau=tau,
draw_probability=draw_probability, backend=backend)
def win_probability(team1, team2, env=None):
env = env if env else trueskill.global_env()
delta_mu = sum(r.mu for r in team1) - sum(r.mu for r in team2)
sum_sigma = sum(r.sigma ** 2 for r in itertools.chain(team1, team2))
size = len(team1) + len(team2)
denom = math.sqrt(size * (env.beta * env.beta) + sum_sigma)
return env.cdf(delta_mu / denom)
for i in range(9):
a = 1/np.sqrt(2)
x0 = env.create_rating(mu=mu, sigma=0.000001)
x1 = env.create_rating(mu=mu+i*50, sigma=0.000001)
x2 = win_probability((x1,), (x0,), env=env)
x3 = np.mean((1+scipy.special.erf(np.sqrt(2)/2*(i*50)/400/a))/2)
x4 = 1/(1+10**(-(i*50)/400))
print(i*50, x2, x3, x4)
--------------------------------------------------------------------
0 0.5000000150000002 0.5 0.5
50 0.5701580945807988 0.5701581024006669 0.5714631174083814
100 0.6381631932475625 0.6381631950841185 0.6400649998028851
150 0.7020584781772754 0.7020584547174111 0.7033850034718286
200 0.7602499538616213 0.7602499389065234 0.7597469266479578
250 0.811620439556852 0.8116204410942089 0.8083176725494586
300 0.8555778081627887 0.8555778168267576 0.8490204427886767
350 0.8920375234793689 0.8920375305299298 0.8823382970469413
400 0.9213503938800034 0.9213503964748575 0.9090909090909091
Trueskillの99.85%分位点
Trueskillのトリックにプレイヤーレートを平均値の$\mu$ではなく、レートを$\mu-3\sigma$で表示するという姑息なトリックがある。これは1000戦のうち最も絶不調でもこれくらいのレートはあるという状態を示す。これを採用すると同時に$\sigma$の大きい新人の開始レートをゼロにすることが出来る(Trueskillの初期設定では$\mu=25,\sigma=8.3333$)ので、半分の人間がレートが下がるしかなくて面白くないという不満を軽減できる。$\sigma$が小さくなればほとんどの人間はレートが上がる。
しかし、厳密な個人レート$\mu$を$\sigma$によってただ隠蔽してるようにも思う。また、試合に勝って$\mu$も上がったのに、$\sigma$が悪化する事でTrueskillのレートが下がるという事が理論上起こりえる。このためレートを$\mu-3\sigma$とすることに関して微妙に思う。以降では平均値の$\mu$をレートとみなしている。
env = trueskill.TrueSkill()
r1 = env.create_rating(mu=100, sigma=10)
r2 = env.create_rating(mu=20, sigma=10)
print('pre_mu=', r1.mu)
print('pre_sigma=', r1.sigma)
print('pre_rate=', env.expose(r1))
(r1,),(r2,), = env.rate(((r1,),(r2,),), ranks=(0,1))
print('after_mu=', r1.mu)
print('after_sigma=', r1.sigma)
print('after_rate=', env.expose(r1))
----------------------------------
pre_mu= 100.0
pre_sigma= 10.0
pre_rate= 70.0
after_mu= 100.0000040206376
after_sigma= 10.00034042803819
after_rate= 69.99898273652303
Trueskillチーム戦
win_probability関数の確認のためチーム戦の勝率を計算してみる。
4人中1人だけ高いとした2vs2の勝率を考えると先ほど計算した勝利確率よりも小さい。
一人だけ実力差がある場合、2vs2での場合は1vs1より$\sqrt{2}$倍高いレートが必要である。
結果は省略するが5vs5のチーム戦において、一人だけ実力差がある場合、1vs1と同じ勝利確率を得るためには1vs1より$\sqrt{5}$倍高いレートが必要である。
一方でチーム戦力は各プレイヤーのレートの相加平均(算術平均)で計算してよくっぽく、同チーム内のプレイヤー人数分ユークリッド距離的足し合わせをする。
$rate_{diff}=\sqrt{\Sigma(T_{1ave}-T_{2ave})^2}$
import trueskill
import numpy as np
import scipy
import itertools
import math
mu = 1200
sigma = mu / 3.
beta = sigma / 2.
tau = sigma / 100.
draw_probability = 0.1
backend = None
env = trueskill.TrueSkill(
mu=mu, sigma=sigma, beta=beta, tau=tau,
draw_probability=draw_probability, backend=backend)
def win_probability(team1, team2, env=None):
env = env if env else trueskill.global_env()
delta_mu = sum(r.mu for r in team1) - sum(r.mu for r in team2)
sum_sigma = sum(r.sigma ** 2 for r in itertools.chain(team1, team2))
size = len(team1) + len(team2)
denom = math.sqrt(size * (env.beta * env.beta) + sum_sigma)
return env.cdf(delta_mu / denom)
for i in range(9):
a = 1/np.sqrt(2)
x0a = env.create_rating(mu=mu, sigma=0.000001)
x0b = env.create_rating(mu=mu, sigma=0.000001)
x0c = env.create_rating(mu=mu, sigma=0.000001)
x1a = env.create_rating(mu=mu+i*50, sigma=0.000001)
x1b = env.create_rating(mu=mu+i*50*np.sqrt(2), sigma=0.000001)
x2a = win_probability((x1a,x0b), (x0a,x0c), env=env)
x2b = win_probability((x1b,x0b), (x0a,x0c), env=env)
x3 = np.mean((1+scipy.special.erf(np.sqrt(2)/2*(i*50)/400/a))/2)
x4 = 1/(1+10**(-(i*50)/400))
print(i*50, x2a, x2b, x3, x4)
--------------------------------------------------------------------
0 0.5000000150000002 0.5000000150000002 0.5 0.5
50 0.5497382394142595 0.5701580945807988 0.5701581024006669 0.5714631174083814
100 0.5987063080237229 0.6381631932475629 0.6381631950841185 0.6400649998028851
150 0.6461697694065315 0.7020584781772753 0.7020584547174111 0.7033850034718286
200 0.6914624830813982 0.7602499538616213 0.7602499389065234 0.7597469266479578
250 0.7340144927338084 0.811620439556852 0.8116204410942089 0.8083176725494586
300 0.7733726582579102 0.8555778081627885 0.8555778168267576 0.8490204427886767
350 0.8092130462669218 0.8920375234793689 0.8920375305299298 0.8823382970469413
400 0.8413447386043253 0.9213503938800034 0.9213503964748575 0.9090909090909091
勝敗判定、引き分けについて
ここでTrueskillのranksは試合順位であり勝利確率とかではない。
だから$(0.3,0.7)$とか小数を突っ込んで辛勝、惜敗を表現しようとしても上手く行かない。
また、値が同じ値の場合は引き分けを示す。
r1 = env.create_rating()
r2 = env.create_rating()
print('(r1,r2)=', (r1,r2))
(r1a,),(r2a,), = env.rate(((r1,),(r2,),), ranks=(0,1))
(r1b,),(r2b,), = env.rate(((r1,),(r2,),), ranks=(1,0))
(r1c,),(r2c,), = env.rate(((r1,),(r2,),), ranks=(0,0))
(r1d,),(r2d,), = env.rate(((r1,),(r2,),), ranks=(0.3,0.7))
print('(r1a,r2a)=', (r1a,r2a))
print('(r1b,r2b)=', (r1b,r2b))
print('(r1c,r2c)=', (r1c,r2c))
print('(r1d,r2d)=', (r1d,r2d))
------------------------------------------
(r1,r2)= (trueskill.Rating(mu=1200.000, sigma=400.000), trueskill.Rating(mu=1200.000, sigma=400.000))
(r1a,r2a)= (trueskill.Rating(mu=1411.000, sigma=344.231), trueskill.Rating(mu=989.000, sigma=344.231))
(r1b,r2b)= (trueskill.Rating(mu=989.000, sigma=344.231), trueskill.Rating(mu=1411.000, sigma=344.231))
(r1c,r2c)= (trueskill.Rating(mu=1200.000, sigma=309.961), trueskill.Rating(mu=1200.000, sigma=309.961))
(r1d,r2d)= (trueskill.Rating(mu=1411.000, sigma=344.231), trueskill.Rating(mu=989.000, sigma=344.231))
イロレーティングは引き分けの場合のレート移動を厳密な意味では定義出来てなかったが、Trueskillでは定義出来ている。
もっともイロレーティングの更新式は
勝った時、$R_{new}=R + K * W_{BA} $
負けた時、$R_{new}=R - K * W_{AB} $
であるから、これは
勝った時、$R_{new}=R + K * (1-W_{AB}) $
負けた時、$R_{new}=R + K * (0-W_{AB}) $
と置けるため、更新式を$R_{new}=R + K * (s-W_{AB})$とした時、$s=1/2$の値が引き分け時のレート移動となろう。また、$s=0.7$とかなら辛勝、$s=0.3$とかなら惜敗と出来るはずである。
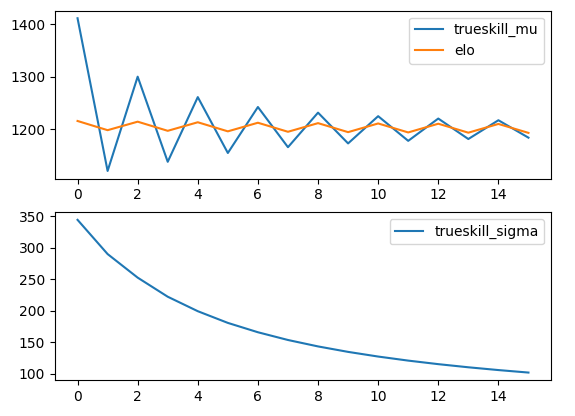
Trueskillのmu、sigmaの推移
仮に勝ったり負けたりを交互に繰り返す場合を考え、その場合のEloScoreとTrueskillのmuとsigmaをplotしてみる。
Eloスコア差があまりない場合、Eloスコアの変動量は勝った場合も負けた場合もほぼ同じで1200付近をうろうろしている。
一方、trueskillは勝ち負けを交互に繰り返しているだけだが、特に最初の方において変動量が大きい。しかし、次第に変動量は小さくなる。
r1 = env.create_rating()
r2 = env.create_rating()
print('(r1,r2)=', (r1,r2))
x = []
y1 = []
y2 = []
for i in range(16):
(r1,),(r2,), = env.rate(((r1,),(r2,),), ranks=(i%2,(i+1)%2))
print(i, ':(r1,r2)=', (r1,r2))
x.append(i)
y1.append(r1.mu)
y2.append(r1.sigma)
r1_elo = 1200
r2_elo = 1200
y1_elo = []
for i in range(16):
K = 32
W_AB = 1/(1+10**(-(r1_elo-r2_elo)/400))
W_BA = 1 - W_AB
if i%2 in list(range(2-1)):
r1_elo = r1_elo + K * W_BA
r2_elo = r2_elo - K * W_BA
else:
r1_elo = r1_elo - K * W_AB
r2_elo = r2_elo + K * W_AB
y1_elo.append(r1_elo)
import matplotlib.pyplot as plt
fig = plt.figure()
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
ax1.plot(x, y1, label='trueskill_mu')
ax1.plot(x, y1_elo, label='elo')
ax1.legend()
ax2.plot(x, y2, label='trueskill_sigma')
ax2.legend()
plt.show()
3回に2回勝つを繰り返す場合、以下の様に収束する。
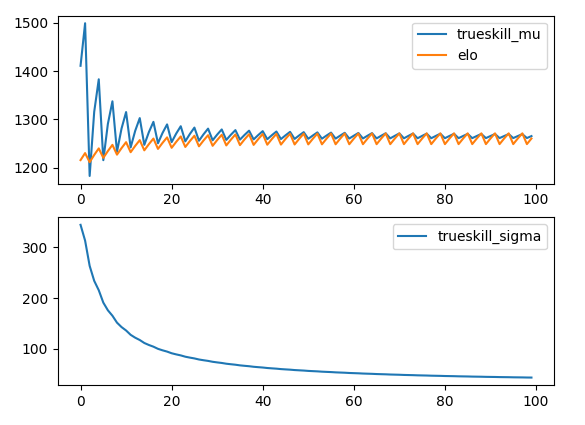
10回に9回勝つを繰り返す場合、以下の様に収束する。
(連続9回勝って1回負けるを周期的に繰り返す)
初期値1200、勝つ方は1400で負ける方は1000なのでレート差は400での勝率91%と大体合う。

従って2者間の収束を調べた限りではeloはレート差が大きいほど収束に回数が掛かるが、Trueskillは比較的早期で平均値は収束する。一方で、ごく初期において非常にノイズが大きく見える。また、$\sigma$も無限に小さくなるわけではなく、ある程度の値で収束する。スコアが収束が中央から離れるほど$\sigma$の収束は大きくなる。
$\mu=1200$付近では$\sigma=37.348$の収束を示したが、
$\mu=1400$では$\sigma=43.516~43.766$の収束だった。
ただし、これは$\mu$に依存するというよりは勝率によるものだろう。二人のプレイヤーが共に$\mu=1400$で交互に勝つ場合は小さくなるだろう。
マッチング品質
qualityはマッチングの品質を示す。$\sigma$の値が大きいプレイヤー(マッチ不足でレートが収束していない)はレートが大きくずれててもマッチ品質にそれほど差はない。$\sigma$の値が小さいプレイヤー(十分マッチ回数をこなしレートは収束している)はレートが400以上大きくずれてると途端に悪くなる。
import trueskill
mu = 1200.
sigma = 400.
beta = 200.
tau = sigma / 100.
draw_probability = 0.1
backend = None
env = trueskill.TrueSkill(
mu=mu, sigma=sigma, beta=beta, tau=tau,
draw_probability=draw_probability, backend=backend)
print('sigma=400')
for i in [0,50,100,150,200,250,300,350,400,800]:
r1 = env.create_rating(mu=1200+i, sigma=0.00001)
r2 = env.create_rating(mu=1200, sigma=400)
q = env.quality(((r1,),(r2,),))
print(i, q)
print()
print('sigma=100')
for i in [0,50,100,150,200,250,300,350,400,800]:
r1 = env.create_rating(mu=1200+i, sigma=0.00001)
r2 = env.create_rating(mu=1200, sigma=100)
q = env.quality(((r1,),(r2,),))
print(i, q)
print()
print('sigma=20')
for i in [0,50,100,150,200,250,300,350,400,800]:
r1 = env.create_rating(mu=1200+i, sigma=0.00001)
r2 = env.create_rating(mu=1200, sigma=20)
q = env.quality(((r1,),(r2,),))
print(i, q)
--------------------------------------------------------------
sigma=400
0 0.5773502691896256
50 0.5743510537743144
100 0.5654465660311143
150 0.5509114754598461
200 0.5311878904526514
250 0.5068630259520308
300 0.47864018454749213
350 0.44730505043732266
400 0.41368954504257255
800 0.15218787864872985
sigma=100
0 0.9428090415820628
50 0.9298049865387412
100 0.8918591402554648
150 0.8320260589249215
200 0.754942463402906
250 0.6662343855826489
300 0.5718425899738045
350 0.4773777974508589
400 0.3876003845956884
800 0.026931812416993713
sigma=20
0 0.9975093361076323
50 0.9821207307600668
100 0.9373647244378631
150 0.8672576745394539
200 0.7778278983192091
250 0.6762615545238773
300 0.5699564849317068
350 0.4656552660008733
400 0.36879341363095347
800 0.018637245146010863
$\sigma=100$と$\sigma=20$でほとんど差はないのは$\beta=200$の値が支配的で影響の小さいためだろう。
$\sqrt{2*200^2/(2*200^2+400^2)}=0.57735..$であるのでqの最大値成分は論文の通りであるのが確認できる。
以下グラフはプレイヤーの内、一人は$\sigma$が非常に小さい、もう一人は$\sigma=[20,100,200,400]$のばらつきを持つ場合の、グラフ横軸は二人のプレイヤーのレート差で、縦軸はマッチング品質である。
レート差200の場合の勝率は76%:24%で品質$\sqrt{2/3}=0.816$、レート差100の場合64%:36%で品質$\sqrt{8/9}=0.943$であるのでこの品質を目安にマッチングを行えば、プレイヤーごとに$\mu ,\sigma$が違っていてもマッチング勝率予測を良く計算できる。
マッチング品質の高いプレイヤーペアからマッチングしていくと$\sigma$が大きいプレイヤー(レートをほとんど戦ってないプレイヤー)はいつまでたってもマッチングしない事になる。しかし、結局はどこかで戦うのでとっとと平均レートプレイヤーとマッチさせた方がよい(対戦相手は嬉しくないだろうが)。間違っても同じマッチングの残り物である上位プレイヤーと対戦させてはいけない。
10人のプレイヤーを5vs5に分ける
Trueskillレートが分かっているならこの場合、全通り計算すればよいように思う。$\frac{{}_{10} C_5}{2}=126$だから計算できなくはない。
これが100人のプレイヤーを50vs50に分ける場合や60人のプレイヤーを3組ずつ20チーム分ける場合、組み合わせ数が膨大で全通りの計算が現実的でない。従ってその場合は動的計画法が必要となるが、10人のプレイヤーを5vs5に分ける程度では全通り計算でもよいだろう。
従って10人のプレイヤーから5人を選ぶ適当なサンプリングを300回も繰り返せばおおよそのチーム分けは可能である。
ただし最適に到達しない可能性は$(\frac{125}{126})^{300}=0.0916$で10%弱ある。
次善の値にも到達しない確率は$(\frac{124}{126})^{300}=0.00823$で1%弱になる。
なお$(\frac{125}{126})^{126}=0.3664..\simeq e^{-1}=0.3679..$である。
import numpy as np
import random
def team_split(member):
mean_score = np.mean(member)
best_score = 10000000
for i in range(300):
team = random.sample(member, 5)
team_mean_score = np.mean(team)
if np.abs(team_mean_score - mean_score) < best_score:
best_score = np.abs(team_mean_score - mean_score)
best_team = team
for i in best_team:
member.remove(i)
return best_team, member
p = [1500, 1525, 1645, 1355, 1785, 1435, 1535, 1475, 1275, 1805]
p_mean = np.mean(p)
team1, team2 = team_split(p)
print(p_mean, team1, np.mean(team1), team2, np.mean(team2))
----------------------------------------------
1533.5 [1435, 1785, 1645, 1275, 1525] 1533.0 [1500, 1355, 1535, 1475, 1805] 1534.0
一応、PuLPを使っても解いてみるが、鶏を割くに焉んぞ牛刀を用いんというやつである。
しかも同じ問題を100回解かせたところ、PuLPが6[s]だったのに対して前述のコードの方が0.7[s]程度と速度面でも特に利点がない。
from pulp import LpProblem, LpMinimize, LpVariable, LpBinary, value, lpSum, lpDot
import numpy as np
p = [1500, 1525, 1645, 1355, 1785, 1435, 1535, 1475, 1275, 1805]
p_mean = np.mean(p)
m = LpProblem("", LpMinimize)
x = [LpVariable("x%d"%i, cat=LpBinary) for i in range(10)]
sum_var = LpVariable('sum_var')
abs_sum_var = LpVariable('abs_sum_var')
m += abs_sum_var
m += sum_var == lpDot(p, x) - p_mean*5
m += abs_sum_var >= sum_var
m += abs_sum_var >= -sum_var
m += lpSum(x) == 5
m.solve()
x2 = [value(x[i]) for i in range(10)]
s = np.sum(np.array(p) * np.array(x2))
t = np.sum(np.array(p) * (1 - np.array(x2)))
print(x2)
print(p_mean, s/5, t/5)
----------------------------------------------
[0.0, 1.0, 1.0, 0.0, 1.0, 1.0, 0.0, 0.0, 1.0, 0.0]
1533.5 1533.0 1534.0
ダブルイリミネーション
あまりレーティングと関係ないが述べておく。
勝ち残り式トーナメント方式のダブルイリミネーションは2敗するまで残れるトーナメントである。
決勝をBO1とするか、勝者サイドが1勝でのBO2とするか、BO3とするかはトーナメントの方針による。以下議論ではBO2とする。
総試合数の見積もりは簡単でシングルイリミネーションでは1試合につき1チームが敗退するので$n$チームが存在する場合、総試合数は$n-1$、試合ステップは$\log_2n$である。
同様にダブルイリミネーションでは総試合数は$2(n-1)$、試合ステップは$2\log_2n+1$である。
ダブルイリミネーションでも勝敗結果が実力通りでも組み合わせが悪いと8人のトーナメントで実力4位のチームの結果が7・8位になることはある(最初の2戦が1,2,3位で2敗した場合)。
8人トーナメントでこれを解消するにはトリプルイリミネーションにするしかなくその時の試合数は総試合数は$3(n-1)$、試合ステップは$3\log_2n+3$となろう。しかし、敗者の試合組み合わせは複雑である。また決勝も1敗と1敗ならBO1となり、1敗と2敗なら勝者サイドが1勝でのBO2となるが、0敗と2敗が決勝の場合は勝者サイドが2勝でのBO3となる。また、トリプルイリミネーションでは最短優勝チームは大会時間の約$2/3$を暇する。
m回イリミネーションでは総試合数は$m(n-1)$となり、組み合わせの悪さを解消するなら$m=\log_2n$のm回イリミネーションが必要なのではないだろうか。
$n=8$の場合$n\log_2n=24$である。
一方で以下の資料では重さの異なる8個の小石と天秤4台を使った場合、図のような組み合わせで示されている。
これによれば1戦目は適当。2戦目は1勝同士と1敗同士を対戦するようにし、3戦目は2勝同士、1勝1敗同士が2戦、2敗同士で戦う。この結果で1位と8位は決定し、以降試合をすることは無い。
4戦目①は暫定2位と暫定3位の戦い、および暫定6位と暫定7位の戦いである。4戦目②は暫定3位と暫定4位の戦い、および暫定5位と暫定6位の戦いである。これは3戦目の結果によって分岐すると思われる。同じリーグが2勝していれば暫定1,3,5,7位に割り振り、2敗リーグを暫定2,4,6,8位にして4戦目①に、同じリーグが1勝1敗の場合は暫定1,3,6,8位か暫定2,4,5,7位にして4戦目②に。
5、6戦目の対戦相手と暫定順位は4戦目の結果次第。4戦目②での暫定3位が4戦目以降3連敗すれば6位まで落ちることもありうるし、暫定6位が4戦目以降3連勝すれば3位になる事もありうる。
前半の展開はダブルイリミネーションと近く見えるがこれは厳密には最下位トーナメントをやってる。後半4~6試合は2位から7位の順位付けに費やしている。トリプルイリミネーションより少ない(ダブルイリミネーションと同等の)試合ステップで8個の小石の順位を評価している利点がある、一方で同時に順位を決定するまでの総試合は多分変わらない。欠点としては最初の一戦の比重が大きく、後半戦は勝っても精々1しか順位が上がらない。最初1回負けるとあと全勝しても4,5位になる事もある。特に他のプレイヤーの結果に左右され自分に勝ったプレイヤーが負け続けると自分も負けた扱いになる。
3戦目までを書くと以下である。同じ組み合わせの場合は試合省略。
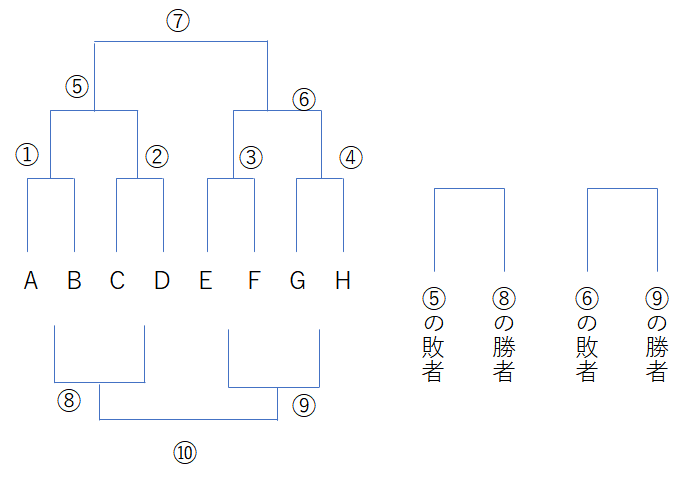
野球のTrueskill
以下の記事を参考に自分の方でもTrueskillの計算をしてみたい。データはこれ。
import trueskill
import pandas as pd
import numpy as np
df = pd.read_csv('./npb_data_2019.csv')
print(df)
mu = 1200.
sigma = mu / 3.
beta = sigma / 2.
tau = sigma / 100.
draw_probability = 0.1
backend = None
env = trueskill.TrueSkill(
mu=mu, sigma=sigma, beta=beta, tau=tau,
draw_probability=draw_probability, backend=backend)
teams = [
'Giants', 'Swallows', 'BayStars', 'Dragons', 'Tigers', 'Carp',
'Fighters', 'Eagles', 'Lions', 'Marines', 'Buffaloes', 'Hawks',]
x = []
y = {}
rate_dict = {}
for team in teams:
rate_dict[team] = env.create_rating()
y[team] = []
for index in df['index']:
home = df['home'][index]
visitor = df['visitor'][index]
hscore = df['hscore'][index]
vscore = df['vscore'][index]
if hscore > vscore:
ranks = (0,1)
elif hscore == vscore:
ranks = (0,0)
elif hscore < vscore:
ranks = (1,0)
r1 = rate_dict[home]
r2 = rate_dict[visitor]
(r1,),(r2,), = env.rate(((r1,),(r2,),), ranks=ranks)
rate_dict[home] = r1
rate_dict[visitor] = r2
if index%5==0:
x.append(index)
for team in teams:
y[team].append(rate_dict[team].mu)
print(rate_dict)
import matplotlib.pyplot as plt
for team in teams:
plt.plot(x, y[team])
plt.legend(teams, loc='upper left', bbox_to_anchor=(0.85, 1))
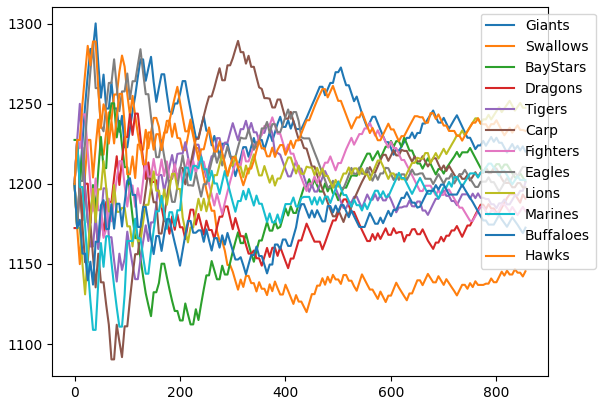
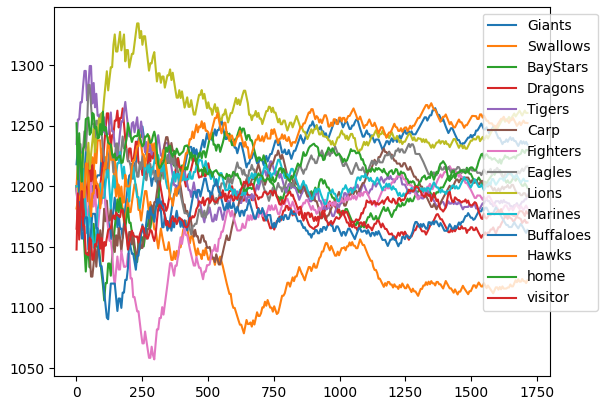
結果は以下の様になった。ここでは本来のTrueskillレートの$\mu-3\sigma$ではなく、単純な$\mu$の推移を示している。収束するのに150試合(チーム当たり25試合)掛かっているように見える。また、参考先も指摘しているようにセ・リーグ 3 位の阪神がセ・リーグ優勝の巨人を抜いている。
{'Giants': trueskill.Rating(mu=1209.889, sigma=39.251), 'Swallows': trueskill.Rating(mu=1144.123, sigma=39.424), 'BayStars': trueskill.Rating(mu=1197.944, sigma=39.161), 'Dragons': trueskill.Rating(mu=1196.346, sigma=39.091), 'Tigers': trueskill.Rating(mu=1213.617, sigma=39.083), 'Carp': trueskill.Rating(mu=1191.340, sigma=39.154), 'Fighters': trueskill.Rating(mu=1171.913, sigma=39.116), 'Eagles': trueskill.Rating(mu=1217.414, sigma=39.019), 'Lions': trueskill.Rating(mu=1271.422, sigma=39.343), 'Marines': trueskill.Rating(mu=1208.833, sigma=39.007), 'Buffaloes': trueskill.Rating(mu=1175.704, sigma=38.916), 'Hawks': trueskill.Rating(mu=1227.130, sigma=38.987)}
正直初期$\sigma=400$がこのモデル(12チームで勝率はある程度拮抗している)においては大きすぎるのかもしれない。$\mu,\beta$そのままで$\sigma,\tau$を1/4にしたときは以下。
この場合はセ・リーグ優勝の巨人がセ・リーグ 3 位の阪神を抜いている。
2位のDeNAのゲーム差は5.5、3位の阪神のゲーム差は6.0、4位の広島のゲーム差は6.5であるから、2~4位の拮抗状況は$\sigma$を小さくしたTrueskillの方が再現出来ている。
{'Giants': trueskill.Rating(mu=1220.271, sigma=29.270), 'Swallows': trueskill.Rating(mu=1145.460, sigma=29.310), 'BayStars': trueskill.Rating(mu=1201.456, sigma=29.100), 'Dragons': trueskill.Rating(mu=1188.251, sigma=29.139), 'Tigers': trueskill.Rating(mu=1203.545, sigma=29.030), 'Carp': trueskill.Rating(mu=1197.874, sigma=29.088), 'Fighters': trueskill.Rating(mu=1182.953, sigma=29.028), 'Eagles': trueskill.Rating(mu=1210.683, sigma=29.022), 'Lions': trueskill.Rating(mu=1247.689, sigma=29.262), 'Marines': trueskill.Rating(mu=1202.517, sigma=28.967), 'Buffaloes': trueskill.Rating(mu=1175.737, sigma=28.955), 'Hawks': trueskill.Rating(mu=1230.108, sigma=29.034)}
ホームの影響度
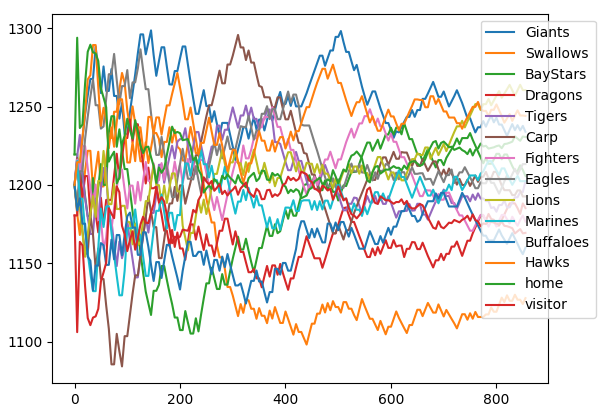
プレイヤーに'home', 'visitor'を追加し、ゲームを2vs2の環境として考える。
homeのレートは1233、visitorのレートは1167なので当然ながらホーム有利であるのが確認できる。またレート差66ある。これはチームのレート差が1位巨人と6位ヤクルトの差が106なのでそれよりは小さい。
import trueskill
import pandas as pd
import numpy as np
df = pd.read_csv('./npb_data_2019.csv')
print(df)
mu = 1200.
sigma = 100.
beta = 200.
tau = sigma / 100.
draw_probability = 0.1
backend = None
env = trueskill.TrueSkill(
mu=mu, sigma=sigma, beta=beta, tau=tau,
draw_probability=draw_probability, backend=backend)
teams = [
'Giants', 'Swallows', 'BayStars', 'Dragons', 'Tigers', 'Carp',
'Fighters', 'Eagles', 'Lions', 'Marines', 'Buffaloes', 'Hawks',
'home', 'visitor']
x = []
y = {}
rate_dict = {}
for team in teams:
rate_dict[team] = env.create_rating()
y[team] = []
for index in df['index']:
home = df['home'][index]
visitor = df['visitor'][index]
hscore = df['hscore'][index]
vscore = df['vscore'][index]
if hscore > vscore:
ranks = (0,1)
elif hscore == vscore:
ranks = (0,0)
elif hscore < vscore:
ranks = (1,0)
r1 = rate_dict[home]
r2 = rate_dict[visitor]
r3 = rate_dict['home']
r4 = rate_dict['visitor']
(r1,r3),(r2,r4), = env.rate(((r1,r3),(r2,r4),), ranks=ranks)
rate_dict[home] = r1
rate_dict[visitor] = r2
rate_dict['home'] = r3
rate_dict['visitor'] = r4
if index%5==0:
x.append(index)
for team in teams:
y[team].append(rate_dict[team].mu)
print(rate_dict)
import matplotlib.pyplot as plt
for team in teams:
plt.plot(x, y[team])
plt.legend(teams, loc='upper left', bbox_to_anchor=(0.85, 1))
plt.show()
{'Giants': trueskill.Rating(mu=1233.913, sigma=39.394), 'Swallows': trueskill.Rating(mu=1127.804, sigma=39.486), 'BayStars': trueskill.Rating(mu=1205.723, sigma=39.281), 'Dragons': trueskill.Rating(mu=1182.351, sigma=39.315), 'Tigers': trueskill.Rating(mu=1205.100, sigma=39.128), 'Carp': trueskill.Rating(mu=1192.647, sigma=39.211), 'Fighters': trueskill.Rating(mu=1176.610, sigma=39.178), 'Eagles': trueskill.Rating(mu=1213.308, sigma=39.228), 'Lions': trueskill.Rating(mu=1260.501, sigma=39.438), 'Marines': trueskill.Rating(mu=1202.393, sigma=39.114), 'Buffaloes': trueskill.Rating(mu=1163.499, sigma=39.098), 'Hawks': trueskill.Rating(mu=1240.533, sigma=39.192), 'home': trueskill.Rating(mu=1232.744, sigma=22.987), 'visitor': trueskill.Rating(mu=1167.256, sigma=22.987)}
Trueskillの疑問、考察
Factor Graph
Trueskillの論文に以下の様な関数が現れる。
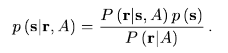
これはベイズの定理の尤度関数として有名である。(自分はあまり分かってないが)

例えとしていかさまコインと通常のコインの2枚があるとする。
いかさまコインの場合は90%表が出る。通常のコインの場合は50%表が出る。
2枚のコインからランダムに選び、それを投げてコインの表が出た場合、これがいかさまコインである確率はいくらか?
Bの事象をいかさまコインを選ぶ確率、Aの事象を選んだコインが表が出る確率とするなら、$P(A|B)$は事象Bが真であるとき事象Aが発生する確率だから$P(A|B)=0.90$、$P(A)=(0.50+0.90)/2$、$P(B)=1/2$より
$P(B|A)=\frac{0.90}{(0.50+0.90)}=0.6429$となるので、事象Aが真であるとき事象Bが発生する確率、つまり表になったコインは64%の確率でこれはいかさまコインである。
この因果の逆な事象確率(事後確率という)を逆算するのは機械学習における誤差逆伝播のように有向グラフを逆順に辿るのに必要かと思った。
パフォーマンスによる勝利確率がばらつき$\beta^2$のシグモイド関数になるためにはプレイヤースキル$s_1$およびばらつき$\sigma^2$は最初にどのようになっているのが尤もらしいかということである。
しかし、Trueskillの実装では以下は動くが、
t1 = (r1,s1,s3)
t2 = (r2,s2,s4)
(t1,t2) = env.rate((t1, t2), ranks=(0,1))
print(t1, t2)
以下の場合は動かない。事後確率計算によってtuple状のgraphツリーの逆順を計算しているのかと思ったが何か勘違いしてるのかもしれない。
t1 = (r1,(s1,s3))
t2 = (r2,(s2,s4))
(t1,t2) = env.rate((t1, t2), ranks=(0,1))
print(t1, t2)
あらかじめ影響度を$0.0<\alpha<1.0$を見積もってenv1の初期設定$\beta_1=\alpha\beta_2$とし、本来の大きさに$\alpha$を掛けて設定すればいいのだろうか。
u1 = (s1,s3)
u2 = (s2,s4)
(u1,u2) = env1.rate((u1, u2), ranks=(0,1))
v1 = env2.create_rating(mu=(u1[0].mu+u1[1].mu)/2, sigma=(u1[0].sigma+u1[1].sigma)/2)
v2 = env2.create_rating(mu=(u2[0].mu+u2[1].mu)/2, sigma=(u2[0].sigma+u2[1].sigma)/2)
t1 = (r1,v1)
t2 = (r2,v2)
(t1,t2) = env2.rate((t1, t2), ranks=(0,1))
print(t1, t2)
Trueskillはゼロサムゲームか?
Trueskillもイロレーティングと同様にゼロサムゲームを目指すはずであると思っていた。
ところがTrueskillはレート移動量は各プレイヤーのばらつき$\sigma$の大きさに依存する。このため異なるばらつき$\sigma$のプレイヤーを対戦すると収束後の$\mu$の平均値が$1200$にならない。
よってこのTrueskillのレート変動はゼロサムゲームを満たさない。
import trueskill
mu = 1200.
sigma = 400.
beta = 200.
tau = sigma / 100.
draw_probability = 0.1
backend = None
env = trueskill.TrueSkill(
mu=mu, sigma=sigma, beta=beta, tau=tau,
draw_probability=draw_probability, backend=backend)
r1 = env.create_rating(mu=1200, sigma=400)
r2 = env.create_rating(mu=1200, sigma=100)
print(r1,r2)
((r1,),(r2,)) = env.rate(((r1,),(r2,)), ranks=(0,1))
print(r1,r2)
for i in range(300):
((r1,),(r2,)) = env.rate(((r1,),(r2,)), ranks=(0,1))
((r1,),(r2,)) = env.rate(((r1,),(r2,)), ranks=(1,0))
print(r1,r2)
------------------------------------------------
trueskill.Rating(mu=1200.000, sigma=400.000) trueskill.Rating(mu=1200.000, sigma=100.000)
trueskill.Rating(mu=1469.987, sigma=305.392) trueskill.Rating(mu=1183.100, sigma=98.765)
trueskill.Rating(mu=1234.926, sigma=37.348) trueskill.Rating(mu=1239.280, sigma=37.348)
以下によれば
Note that the TrueSkill ranking system’s update equation for the mean skill is thus not guaranteed to be zero sum.
TrueSkillランキングシステムの平均スキルの更新式は、このようにゼロサムであることが保証されていないことに注意してください。
機械学習の誤差逆伝播
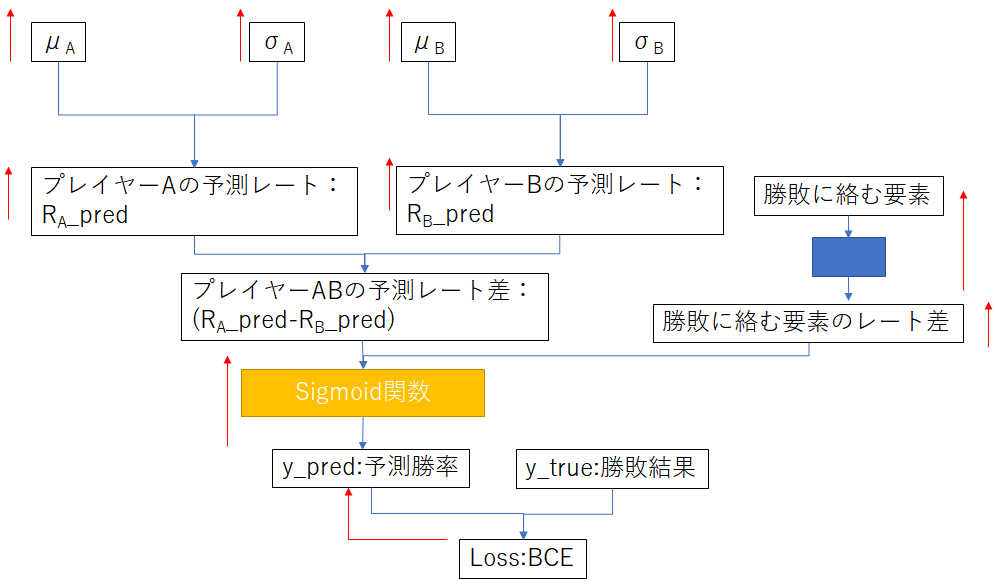
機械学習だと最後の出力層の活性化関数をsigmoid関数にして勝敗に絡む要素(例えばホーム、アウェイとか先攻、後攻とか試合日の風向、天候だとか)の影響のレート差への変換を学習する。また、プレイヤーの予測レートも誤差逆伝播にて更新できよう。
こう考えるとイロレーティングにおけるレートの更新が学習率を一定とした場合の機械学習モデルと類似性を見出せるのではないかと思った。(ただし、$x$を固定化したモデルの重み$W$の更新ではなく重み$W$を固定した場合の入力$x$の値を更新する)。一方で機械学習の学習率は通常1E-3~1E-7くらいでプレイヤー当たり200回程度で収束するイロレーティングよりもずっと小さい。また、機械学習にはAdamのような収束を早めるような更新量を調整する仕組みがあるが、これもイロレーティングでは見当たらない。
またプレイヤーごとの$\mu,\sigma$を更新すればTrueskillに近いのではないかと思った。ただし、$\mu$の平均値を一定の値を維持したい更新をするなら$(\mu-\mu_0)$のL1,L2正則化を考えなければならない。つまり$Loss_{L1}=|\Sigma(\mu_i-\mu_0)|$か$Loss_{L2}=\Sigma(\mu_i-\mu_0)^2$を損失に追加する。Trueskillがゼロサムを満たさないのはこのレート更新にL1,L2正則化項がないからではないだろうか。難しそうに聞こえるかもしれないが、L1損失であれば総プレイヤーの平均が$\mu_0$になる方向に全プレイヤーのレートを同じだけ増やすか減らすだけである。
まあ、深層学習(ディープラーニング)が流行ったのはAlexNetで数えてもせいぜい2012年頃からで、Trueskillの発表された2006年においては多層パーセプトロン的なアイデアは存在はしていたもののおそらくメジャーではなかったろう。
自動チーム分け
仮に100人のプレイヤーがいてそれぞれ1~100の数字が渡されているとする。この中から適当に10人を選び、合計戦力(配られた数字の合計)がなるべく等しいように自動で5vs5に分けるとする。これを繰り返した場合、チーム分け結果のみでプレイヤーの持っている数字を当てられるだろうか、という思考実験。
まず、50位のプレイヤーは当てることができるだろう。このプレイヤーと同じチームになる確率と別チームになる確率は変わらず、51位のプレイヤーだろうと1位のプレイヤーだろうと同程度、味方や敵になる。おそらくチーム分け結果に最も偏りがないプレイヤーである。
一方、1位のプレイヤーは100位と同じチームになる確率が高く、また1位のプレイヤーは2位のプレイヤーと別チームになる確率が高い。
同様に100位のプレイヤーは1位と同じチームになる確率が高く、また100位のプレイヤーは99位のプレイヤーと別チームになる確率が高い。
ただし、ここで1位と100位はチーム分け結果のみではどちらが上か区別がつかないのでこの二人のプレイヤーの内どちらが高いかは知らされるとする。
推測が強くなるが、25位のプレイヤーは1位~50位の50プレイヤーから10人をサンプリングした時チーム分けのばらつきが少なく、75位のプレイヤーは51位~100位の50プレイヤーから10人をサンプリングした時チーム分けのばらつきが少ない。また50位のプレイヤーは再定義する際、26位~75位の50プレイヤーから10人をサンプリングした時チーム分けのばらつきが少ないほうが、ノイズが小さくなるのではないか。同じチームと別チームになる確率を調べていけば効率的に同定できる。このようにサンプリング対象を小さくしながら同定していけば以下25位→12位→6位→…と凡そ同定できるのではないだろうか。(というより100人から10人選ぶ場合、$_{100}C_{10}=1.7×10^{13}$であるから相当数サンプリングしないとノイズが小さくならず効率が悪い。その為、最初に適当に25人くらいで4グループ分けしてその中で暫定順位をつけて、グループを混ぜてその中から25人を取り出すといった事を繰り返すほうがまだ効率が良いかもしれない)
import numpy as np
import random
import matplotlib.pyplot as plt
def team_split(member, check_num):
mean_score = np.mean(member)
member.remove(check_num)
best_score = 10000000
for i in range(300):
team = random.sample(member, 5)
team_mean_score = np.mean(team)
if np.abs(team_mean_score - mean_score) < best_score:
best_score = np.abs(team_mean_score - mean_score)
best_team = team
for i in best_team:
member.remove(i)
return best_team, member
fig = plt.figure()
ax = []
p_list = list(range(100))
y1 = np.zeros((4, 100))
y2 = np.zeros((4, 100))
for index, check_num in enumerate([49, 0, 99, 24]):
print(index)
for i in range(150000):
member = random.sample(p_list, 10)
if not check_num in member:
continue
other_team, same_team = team_split(member, check_num)
for j in same_team:
y1[index, j] += 1
for j in other_team:
y2[index, j] += 1
ax.append(fig.add_subplot(2, 2, index+1))
ax[index].plot(p_list, y1[index], label='same_team')
ax[index].plot(p_list, y2[index], label='other_team')
ax[index].set_title('check_num=%d' % (check_num))
ax[index].legend()
plt.show()
また、前述の考察では自動チーム分けにおいて、上位プレイヤーと下位プレイヤーはチーム分け結果のみではどちらが上か判定できない。特にグループを小さくしていくと、グループ内の上位プレイヤーと下位プレイヤーはどちらが上なのかは判別が付きにくくなるという欠点がある。判別が付くのは常にグループ内の中間プレイヤーだけである。
上位グループの中間プレイヤーを除いた(上の上と上の下)と、中間グループの中間プレイヤー(中の中)をグループとして抜き出せば、上の下を同定できる。
同様に上の中と中の上と中の下を抜き出せば中の上を同定できよう。
同様に偏りを大きい、ほどほど、小さい、ほどほど、大きいの5段階で分割した時、上位グループの偏りが大きいと小さい、中位グループのほどほどを抜き出せば、上位グループの偏りが大きい位置の上下を同定できるだろう。
一方で、1~100の等間隔な数字ではなく、ガウス分布に従うTrueskillなどのレートの場合、チーム分け結果のみで各プレイヤーの内部レートを推定することは可能だろうか?
自分は初期レート差がない場合、引き分け結果のみではレート移動がないためレートを決定するのは無理なのではと思った。
r1 = env.create_rating(mu=1200, sigma=400)
r2 = env.create_rating(mu=1200, sigma=400)
print(r1,r2)
((r1,),(r2,)) = env.rate(((r1,),(r2,)), ranks=(0,0))
print(r1,r2)
---------------------------------------------------
trueskill.Rating(mu=1200.000, sigma=400.000) trueskill.Rating(mu=1200.000, sigma=400.000)
trueskill.Rating(mu=1200.000, sigma=309.961) trueskill.Rating(mu=1200.000, sigma=309.961)
ロールの影響度
5vs5の単純な打ち合いではないゲームなら大体スキルやロールがある。
例えばヒーラーやサポートは勝利貢献度は低いのではと思う(偏見)。この勝利貢献度の低い役職に上級者や初心者を入れても結果に影響を与えづらい。
このような勝負に対するロールの影響度を推定するにはどのようにしたらいいだろうか。
この場合、プレイヤーのレート(推定)とロールの影響度(推定)は足し算ではなく掛け算である。足し算であればTrueskillで推定できる。
Trueskill2ではプレイ時間を掛けている。ロールのない単純な打ち合いゲームならそれでいいんだろうけど役職のあるゲームでは該当しない。

となるとマッチングに関する大量データからロールの影響度は推定せざるを得ないが、大量データがないとロールの影響度は推定できない。
キャラクター習熟度
プレイヤーがあるキャラクターの場合は非常に強く、別のキャラクターの場合は弱い(自キャラまたは対戦キャラごとの習熟度と表現できる)場合に対して考慮できるのだろうか。
これはキャラクターの習熟度を平均0でばらつきのある正規分布を仮定し、この収束値がプラスに収束すれば得意キャラ、マイナスに収束すれば苦手キャラとなる。
しかし、全てのキャラクターの習熟度の総和をゼロとするように移動しないといけないし、その上にキャラクター選択がマッチングの後に選択するタイプのゲームの場合、チームマッチングに寄与しないキャラクターの習熟度を分ける意味はあまりないのではと思う。(予めキャラやロールを選択したうえでマッチングするゲームならキャラクター習熟度は有効かもしれないが)
また、マップやバトルモードに関しても細分化出来る。
ここでいうロールの影響度とキャラクター習熟度を混同するかもしれないが、前者は特定ロールの試合へ貢献影響度でありプレイヤーレートへの掛け算、後者はプレイヤーの得手不得手の補正でありプレイヤーレートへの足し算である。
組み合わせの影響度
TCG(トレーディングカードゲーム)のマッチを考える。この場合、低レート帯ではプレイヤーの上手さや手札運よりもほとんど試合前にデッキのカードパワーで勝負が決定してしまうように思う。
この補正を考えたマッチにするにはプレイヤー1名と先攻後攻を1個、デッキカード40枚の42vs42で考えれば、プレイヤーレート(上手さ)と同様に先行の有利レートや1枚1枚のカードパワーは収束する。このデッキのカードパワーを考えてマッチを行えば、ランク中に途中でデッキを変えても同じデッキのカードパワー同士でマッチングが行えるのではと思った。
一方でカードA単体やカードB単体では弱く、カードAとBが揃った場合は強い場合の組み合わせの影響をTrueskillは考慮できるのだろうか。
これは仲の良いプレイヤーでチームを組んだ場合や仲の悪いプレイヤーでチームを組んだ場合を考えるに等しい。機械学習によればこのようなand回路の重みは入力$x_1,x_2$を0,1の値として以下の計算で実装できる。
y_{and} = relu((0.5,0.5,-0.5)\cdot(x_1,x_2,1))
一方でTrueskillのレート差変換のモデルが単なる線形和しか計算できないのであれば、組み合わせ(and回路)は求められない。
(現在=>過去)=>(過去=>現在)
過去から現在でプレイヤーのスキルが微増しているとする。
この場合、データを繰り返して2倍に増やす行為をすると過去と現在の接合点でレートが一致せずレート変動が不安定になる。そこで時系列を逆順にして繋げれば接合点のレートが一致するため初期$\sigma$のばらつきが収束するまでのノイズを解消できるのではと思った。
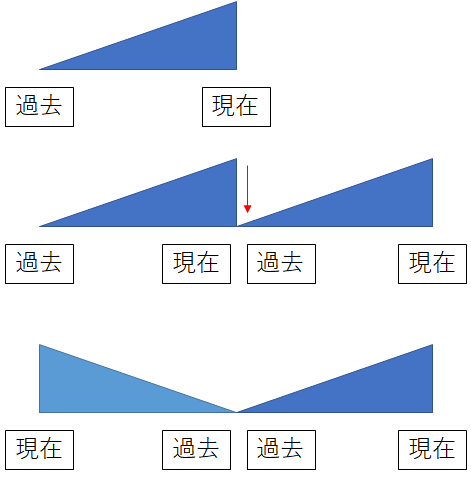
半分の過去時点で最初からヤクルトは最下位から、巨人は高い位置のレートから開始でき、初期のノイズが大きい過程はカット可能である。ただし、逐一計算させるよりも計算量が増えるし、過去の戦歴を参照しなければいけない上、データが収束よりも少ない場合はあまり効果はない。
あえてこの手法のメリットを挙げるとすれば、のちのプロになるプレイヤーにレート1500付近で戦った不運なプレイヤーに対してレート損失を軽減できる。同様に初心者の皮を被った経験者や100回前に戦ったプレイヤーがチーターでBANされた場合もレート損失を補正できる。また、過去にチーター(その後アカウントBAN)が味方にいたブースティング対象のプレイヤーのレートも下げられる等である。
途中退室のペナルティ
Trueskill2の9章でQuit penaltyについて議論している。
途中退室したプレイヤーにペナルティを、完走したプレイヤーに報酬を与えるとある。
しかし、本当の問題は途中退室したプレイヤーはレートが下がる事を真に恐れていない事にある。彼らは勝てない試合を続けるのは時間の無駄と考えており、ただ単に勝てる試合をしたいだけである。従ってレートを上げる事もそれほど望んでいない(または既に諦めている)。経験者のサブ垢や下げランも思考は同じことである。このような途中退室プレイヤーに対しレートを下げる事が問題の解決になるだろうか?彼らがやりたいのは雑魚狩りである。
全てのプレイヤーがレートを上げることを至上命題としていれば問題ないが、勝ちやすくするためレートをわざと下げるプレイヤーがいるのなら、プレイヤーレートとプレイヤー技術の議論は噛み合わなくなる。
また逆に自分の分相応以上にレートを上げる行為に、キャリー、ブースティング、代行がある。しかし、分相応でないプレイヤーはその先の試合で結局負けるだけである。
更に途中退室したプレイヤーに同情的な見方をするなら味方のトロールや暴言プレイヤー、敵の死体撃ちや屈伸煽りなど不快なプレイヤーに対する消極的な抵抗の場合がある。
まあいずれにせよレートに工夫するより、途中退室は10分以上のマッチング禁止時間を設ける方が再発防止の効果はあるのではと思う。
懲罰、褒賞マッチング
前述の途中退出ペナルティは害悪プレイヤーに対して、レートを下げることで同じ害悪プレイヤー同士をマッチングさせるという発想はよいのだが、それに同じ低いレートの初心者が付き合わされるのは途中退室のペナルティをレートに転換する副作用ではないだろうか。
初心者と害悪プレイヤーが同チームになることなく、あくまで害悪プレイヤー同士で同じチームにして、わざと強い相手と戦わせる懲罰マッチングする方法や、チームメンバーに抜けられた優良プレイヤーの害悪プレイヤー除けた密かに勝つ確率の高い相手と戦わせる褒賞マッチングを行うなどをレート以外で実装する方法は議論していない。
この問題は単純なレートだけでマッチングが決定する場合、プレイヤーの罪深さは考慮できないからである。一方、雑魚狩りしか楽しみのない行き詰ったプレイヤーに単に初心者とのマッチングを禁止するように改良すればおそらくこのプレイヤーはもう引退するほかない。
自分が考えるのはあえて不公平なマッチングを採用し、はばらつき$\sigma$が大きい新規プレイヤーと戦わされて負けた既存プレイヤーやレーティングが不正確(過剰にレートを高くしすぎた)せいで連敗したプレイヤーに対してお詫びマッチング(接待試合)を設けるという事も含む。あとは課金者優遇とか。
あとこれはマッチングの不具合に対する詫びを兼ねているため、5人チームでデュオで参加した片方が離脱した場合、残りの三人に対しては補償するが、抜けたプレイヤーの相方に対しては補償しない。
ここでいう補償とはレートを減らさないという意味ではなく、次回のマッチングで勝ちやすい相手と対戦するという意味だけである。
公正世界仮説、ギャンブラーの誤謬
前述のあえて不公平なマッチングを望むのは正しい行いだろうか?
プレイヤーが公平だと感じるマッチングは実は真の公平ではなく、公平なマッチングからプレイヤーの認知バイアスだけずれている。真の世界はもっと非情なのだ。
公正世界仮説では不幸なマッチングに当たるのは前世(前のゲーム)で悪い事をしたからだというバイアスを実現するものである。また、不幸なマッチングに当たったものは来世(次のゲーム)で報われる筈だというバイアスを実現するものである。
また、ギャンブラーの誤謬も連続して負けたなら、次は勝てる確率が通常より高い筈だというバイアスを実現するものである。
このような認知バイアスを実現した方が仮にプレイヤーの求めるマッチングになっていたとしても、それが本当に良い事なのかは議論があるだろう。とはいえ運の下振れたプレイヤーに最低保証や天井を設けることは少なくともプレイヤーの不満を低減するのに効果があるのは実証されている。
また、実際の期待値と人間が感じる期待効用の間に差がある。このような人間の感じる期待効用を論じる理論を期待効用論という。
不正なコインで公正な結果を得る
連敗中のプレイヤーは想定されているレートより下振れているパフォーマンスしか発揮できない。このような3割しか表の出ないコインで1/2を求めるにはどうすればよいか。
ジョン・フォン・ノイマンは次の手順を示した。
- コインを2回トスする。
- 2回の結果が一致する場合は、両方の結果を破棄し、最初からやり直す。
- 2回の結果が一致しない場合は、1回目の結果を採用する。
ある10連敗のプレイヤーの勝率が3割に下がっていたとする。
これを採用するためには10連敗のプレイヤーに別の10連敗のプレイヤーをぶつければどちらが勝っても10連敗のプレイヤー勝率は1/2になる。
ただし、これは10連敗のプレイヤーの勝率が5割よりも下がっていると統計的に確認される場合に有効であり、そんなことは無いのなら補正する必要はない。
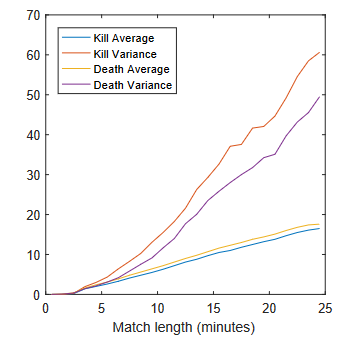
kill,deathカウント
Trueskill2でkill,deathを用いてチームパフォーマンスを決定する。
ここでkill,deathはマッチのプレイ時間にほぼ比例する。
つまり、試合が圧勝でゲーム時間が15分なら平均killカウントは少なく、試合が互角で25分掛かるなら平均killカウントも多くなる。キルデスは試合時間に比例するためこれを時間で割った場合、ゲームに依る定数となる。
kill rateはキル数を時間でわってkill/minuteを求めている。
これはよく知られるK/Dのキルレシオではない。
例えば$perf_{diff}=\alpha \cdot(killrate - c)$のように近似できるかもしれない。
一方で勝率とキル数は非対称のように見える。以下の表によれば勝率50%になるkillrateは1.4くらい。しかし、killrate=0.2の勝率は43%に対して、killrate=2.6の勝率は53%しかない。
つまり、killrate=0.0とかのプレイヤーは実質killrateはマイナスに転じる(味方の足を引っ張る)地雷プレイヤーを含んでいる筈であるが、それはkillrateのみでは判断できない。要するにdeathレートも必要なのではと思う。味方が戦闘する間に陣地を取っていたとかの場合は、killrateは低くても仕方がない。
対面係数
Trueskill2を眺めた時、対面係数なる係数がある。
例えば以下の係数は自チーム内のプレイヤー影響度である。
以下式ではチーム内のプレイヤーのプレイ時間に比例するとしている。

対して対面係数は自チームと敵チームのプレイヤーのプレイ時間との比率を掛ける。
チーム戦だが実態として協力要素が薄く、同じロールの1vs1をずっとやるゲームにおいてはいいのかもしれない。
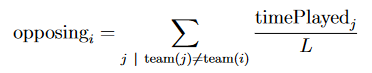
チーム内パフォーマンスと対面パフォーマンスは適当な重みで足し合わせる。この二つの重みがいくらであるべきかはkill、deathのカウントをプレイ時間で割ってkillrateを求め、チーム内パフォーマンスと対面パフォーマンスから重みをチューニングする。
練習問題
適当なkaggleのデータからkill、deathレートの係数を求めてみたい。
データの内、df['blueKills']、df['blueDeaths']、df['blueTotalGold']、df['redTotalGold']およびdf['blueWins']のみ使う。ゲームの試合時間=blueGold + redGoldで近似できるとしてblueKill、blueDeathsを試合時間で割る。レート差を$rate_{diff_1}=a*(blueKill/time-c)$と$rate_{diff_2}=-b*(blueDeath/time-c)$の和と置く。$(a,b,c)=[1.68831851e+06,1.76868333e+06,1.54275318e-04]$となる。
x_predの大きさ順に実際の勝敗結果yをsortし、37点毎に平均を取って267点をplotすると以下の様になった。青の点がシグモイド関数になっているのはy_predがx_predのシグモイド関数としてそもそも定義しているため。オレンジの点は実際の勝敗yのx_pred順の37点ごとの平均。
このように大規模データから事前に係数を見積もっておき、このweightを利用してチームパフォーマンス(perf)を計算して仮想チームレート差から個人レートを収束させると良いのではないだろうか。
from scipy.optimize import curve_fit
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv('./high_diamond_ranked_10min.csv')
def func(x,a,b,c):
blueKill = x[0]
blueDeath = x[1]
blueGold = x[2]
redGold = x[3]
total_gold = blueGold + redGold
blueKillperGold = blueKill / total_gold
blueDeathperGold = blueDeath / total_gold
rate_diff1 = a*(blueKillperGold - c)
rate_diff2 = -b*(blueDeathperGold - c)
rate_diff = rate_diff1 + rate_diff2
blue_Win = 1/(1+10**(-rate_diff/400))
return blue_Win
x = []
y = []
for index in df.index:
x.append([df['blueKills'][index], df['blueDeaths'][index], df['blueTotalGold'][index], df['redTotalGold'][index]])
y.append(df['blueWins'][index])
x = np.array(x).T
y = np.array(y)
print(x.shape)
print(y.shape)
param, cov = curve_fit(func, x, y)
print('param=', param)
def func2(x,a,b,c):
blueKill = x[0]
blueDeath = x[1]
blueGold = x[2]
redGold = x[3]
total_gold = blueGold + redGold
blueKillperGold = blueKill / total_gold
blueDeathperGold = blueDeath / total_gold
rate_diff1 = a*(blueKillperGold - c)
rate_diff2 = -b*(blueDeathperGold - c)
rate_diff = rate_diff1 + rate_diff2
blue_Win = 1/(1+10**(-rate_diff/400))
return rate_diff, blue_Win
x_pred = []
y_pred = []
for index in df.index:
x_pred_one, y_pred_one = func2(x[:,index], param[0], param[1], param[2])
x_pred.append(x_pred_one)
y_pred.append(y_pred_one)
x_pred_orig = np.array(x_pred)
zip_lists = zip(x_pred, y)
zip_sort = sorted(zip_lists)
x_pred, y = zip(*zip_sort)
x_pred = np.mean(np.reshape(x_pred, (267,37)), axis=1)
y = np.mean(np.reshape(y, (267,37)), axis=1)
plt.scatter(x_pred_orig, y_pred)
plt.scatter(x_pred, y)
plt.scatter(400, 0.909)
plt.show()
---------------------------------------------
(4, 9879)
(9879,)
param= [1.68831851e+06 1.76868333e+06 1.54275318e-04]
あとで気付いたがこのデータはゲーム開始10分時点でのKill、DeathなのでGoldで割る理論的な意味はあまりないのかもしれない。後この関数はほとんど(kill-death)差に依存する単純関数である。また、curve_fitがどういう最適化をしてるのか知らないが今回はシグモイド関数なのでmseよりはbinary cross entropyを損失関数にした方が本当はよいだろう。
また(kill-death)差以外にDragon差、Herald差、Tower差の変数を増やした関数にてフィッティングを行った場合、400レート差で勝率91%になるとして1(kill-death)差で50、1Dragon差で52、1Herald差で28、1TowersDestroyed差で72レートに相当する係数となった。
勝利確率がほぼ線形に比例していると仮定するなら最終的な勝利確率は「10分時点」での1(kill-death)差で5%、1Dragon差で5%、1Herald差で3%、1TowersDestroyed差で7%増加する。
ゲームをあまり知らないのでこれが合っているのかはよく分からない。
def func(x,a,b,c,d,e,f):
blueKill = x[0]
blueDeath = x[1]
blueGold = x[2]
redGold = x[3]
blueDragons = x[4]
redDragons = x[5]
blueHeralds = x[6]
redHeralds = x[7]
blueTowersDestroyed = x[8]
redTowersDestroyed = x[9]
total_gold = blueGold + redGold
blueKillperGold = blueKill / total_gold
blueDeathperGold = blueDeath / total_gold
rate_diff1 = a*(blueKillperGold - c)
rate_diff2 = -b*(blueDeathperGold - c)
rate_diff3 = d * (blueDragons - redDragons)
rate_diff4 = e * (blueHeralds - redHeralds)
rate_diff5 = f * (blueTowersDestroyed - redTowersDestroyed)
rate_diff = rate_diff1 + rate_diff2 + rate_diff3 + rate_diff4 + rate_diff5
blue_Win = 1/(1+10**(-rate_diff/400))
return blue_Win
----------------------------------------
param= [1.53425049e+06 1.63542878e+06 1.70552776e-04 5.22961619e+01
2.82415481e+01 7.16541441e+01]
不確定性
Trueskill自身にレートに掛け算となる重み係数を決定する能力はおそらくなく、対象のゲームに対して事前に大規模データから重み係数を求める(または試合チーム内のプレイ時間や対面とのプレイ時間比から係数を近似する)必要があるように思う。素人考えだがプレイヤーのレート$r$とゲームの重み係数$w$は同時に決定できないのではと思った($perf=r\cdot w$のばらつきは分かったとしても)。例えば機械学習では$y=Wx$としてxを固定してWを更新する。逆にレーティングではWを固定してxを更新する。
これは量子力学の不確定性原理で位置$x$と運動量$p$が同時に決定できないのと似たような理屈かもしれない。不確定性原理では位置の分散$\Delta x$と運動量の分散$\Delta p$に対して$\Delta x \Delta p \geq \frac{\hbar}{2}$である。
Trueskillのレート更新量
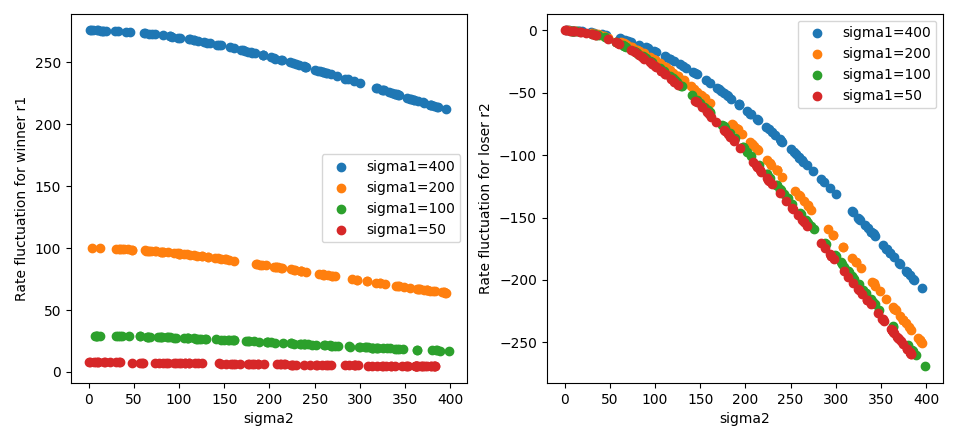
大分話が脱線するため一番最後に書くが、Trueskillのゼロサムゲームの項にての考察である。
r1とr2が同レートでsigma1、sigma2が異なる時、勝者のr1と敗者のr2のレート変動量をプロットしてみた。r1のレート変動量はsigma1に大きく依存しており、r2のレート変動量はsigma2に大きく依存しているのが確認できる。
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
for sigma1 in [400, 200, 100, 50]:
x = []
y1 = []
y2 = []
for i in range(100):
sigma2 = 400*np.random.rand()
r1 = env.create_rating(mu=1200, sigma=sigma1)
r2 = env.create_rating(mu=1200, sigma=sigma2)
((r1a,),(r2a,)) = env.rate(((r1,),(r2,)), ranks=(0,1))
x.append(sigma2)
y1.append(r1a.mu-r1.mu)
y2.append(r2a.mu-r2.mu)
ax1.scatter(x, y1, label='sigma1=%d' % sigma1)
ax2.scatter(x, y2, label='sigma1=%d' % sigma1)
ax1.legend()
ax1.set_xlabel('sigma2')
ax1.set_ylabel('Rate fluctuation for winner r1')
ax2.legend()
ax2.set_xlabel('sigma2')
ax2.set_ylabel('Rate fluctuation for loser r2')
plt.show()
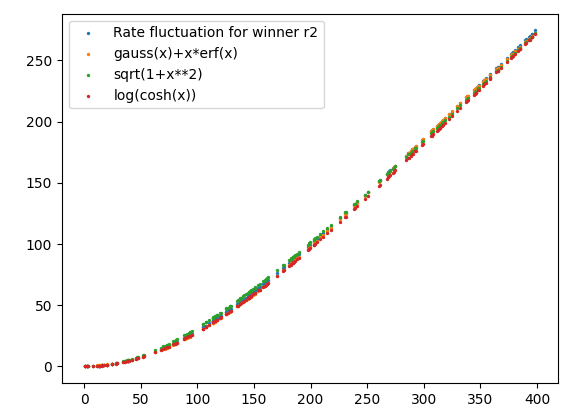
ここでxが小さい値で2次、大きい値で1次で変動する関数を推測したい。もちろん有名なのは$\sqrt{1+x^2}$とかであるが。正規分布の関連を思い浮かべると$f(x)=Gauss(x)+x\cdot \Phi(x)$である。$\Phi(x)$は正規分布の累積分布関数$(\Phi(x)=\frac{1+erf(x)}{2})$。$\Phi'(x)=Gauss(x)$かつ$Gauss'(x)=-x \cdot Gauss(x)$であるから、$f'(x)=Gauss'(x)+x\cdot \Phi'(x)+\Phi(x)=\Phi(x)$である。なお機械学習では$GELU(x)=x\cdot \Phi(x)$として知られる。また$\log(1+\exp(x))$はsoftplus関数である。
しかし、これが前述の更新式と関連する事は示せなかった。 適当に係数を決めれば近づく関数はfit出来るがそれだけなら$\sqrt{1+x^2}$でもよい。
なお$Gauss(x)+x\cdot \Phi(x)$、$(x+\sqrt{1+x^2})/2$、$\log(1+\exp(x))$のいわゆるrelu型(softplus型)関数で、一階微分はシグモイド型の関数、それぞれの二階微分は、ガウス分布、$\nu=2$のt分布、ロジスティック分布である。
tanh型を積分した双曲線型関数なら、$Gauss(x)+x\cdot erf(x)$、$\sqrt{1+x^2}$、$\log(\cosh(x))$となろう。
import scipy
x = []
y1 = []
y2 = []
y3 = []
y4 = []
for i in range(200):
x1 = 400*np.random.rand()
r1 = env.create_rating(mu=1200, sigma=0.000001)
r2 = env.create_rating(mu=1200, sigma=x1)
((r1a,),(r2a,)) = env.rate(((r1,),(r2,)), ranks=(1,0))
z1 = r2a.mu-r2.mu
z2 = 1/np.sqrt(2*np.pi)*np.exp(-x1/400*x1/400/2) + x1/np.sqrt(1.95) * scipy.special.erf(x1/400*np.sqrt(2))
z3 = 400*(np.sqrt(1+x1/400*x1/400*9)-1)/np.sqrt(9+1)
z4 = 400/2.8*np.log(np.cosh(x1/400*2.6))
x.append(x1)
y1.append(z1)
y2.append(z2)
y3.append(z3)
y4.append(z4)
plt.scatter(x,y1,s=2, label='Rate fluctuation for winner r2')
plt.scatter(x,y2,s=2, label='gauss(x)+x*erf(x)')
plt.scatter(x,y3,s=2, label='sqrt(1+x**2)')
plt.scatter(x,y4,s=2, label='log(cosh(x))')
plt.legend()
plt.show()
| 分布関数 | sigmoid型関数 | relu型関数 | tanh型関数 | 双曲線型関数 |
|---|---|---|---|---|
| デイラックのデルタ関数 | ヘヴィサイドの階段関数 $(1+sgn(x))/2$ $=(1+\frac{|x|}{x})/2$ |
relu関数 $(x+|x|)/2$ |
$sgn(x)$ $=\frac{|x|}{x}$ |
$|x|$ |
| ロジスティック分布 $\frac{e^{-x}}{(1+e^{-x})^2}$ $=sech^2(x/2)$ |
シグモイド関数 $(1+tanh(x/2))/2$ $=\frac{1}{1+e^{-x}}$ |
softpluse関数 $\log(1+e^x)$ |
$tanh(x/2)$ | $2\log(\cosh(x/2))$ |
| 正規分布(ガウス分布) $\frac{1}{\sqrt{2\pi}}exp(-x^2/2)$ $=Gauss(x)$ |
正規分布の累積分布関数 $(1+erf(x/\sqrt{2}))/2$ $=\Phi(x)$ |
$Gauss(x)+x\Phi(x)$ | $erf(x/\sqrt{2})$ | $Gauss(x)+x\cdot erf(x/\sqrt{2})$ |
| $\nu=2$のt分布 $\frac{1}{(1+x^2)^{\frac{3}{2}}}$ |
$(1+\frac{x}{\sqrt{1+x^2}})/2$ | $(x+\sqrt{1+x^2})/2$ | $\frac{x}{\sqrt{1+x^2}}$ | $\sqrt{1+x^2}$ |
| 一様分布 | hard_sigmoid $clip((1+x)/2,0,1)$ |
- | $clip(x,-1,1)$ | $(1+x^2)/2 …(|x|<1)$ |
| 双曲線正割分布 $sech(\frac{\pi}{2}x)/2$ |
$(1+\frac{2}{\pi}gd(\frac{2}{\pi}x))/2$ | - | $\frac{2}{\pi}gd(\frac{2}{\pi}x)$ | - |
| ローレンツ分布 $\frac{1}{\pi(1+x^2)}$ |
$(1+\frac{2}{\pi}arctan(x))/2$ | $x(1+\frac{2}{\pi}arctan(x))/2-\frac{\log{(1+x^2)}}{2\pi}+C$ | $\frac{2}{\pi}arctan(x)$ | - |
| $\frac{1}{2(1+|x|)^2}$ | $(1+\frac{x}{1+|x|})/2$ | - | softsign関数 $\frac{x}{1+|x|}$ |
- |
| 任意分布 (sigmoid型関数の微分) |
任意分布の累積分布関数 (任意分布の積分) (relu型関数の微分) |
sigmoid型関数の積分 (任意分布の二階積分) |
2*sigmoid型関数-1 | tanh型関数の積分 |
…と長々と妄想を書いた。
まとめ
イロレーティングの考察の続きとTrueskillについて調べた。
イロレーティングよりTrueskillの方がやや難しい。イロレーティングは単純な1vs1しかできないが、Trueskillは単純なチーム戦であればレーティング出来る。Trueskillは2006年に発表されており、論文内で試されたゲームがHalo 2とかいうゲームだが20年前のゲームでよく知らない。2018年のTrueskill2でもHalo5と同じシリーズのゲームについて議論している。調べた感じCoDやBFみたいな小隊のあるFPSゲームなのだと思う。
一方で、最近のロールのあるチーム戦を考える上ではTrueskillはまだ力不足であるように思った。Trueskill2では様々な補正を加えるテクニックを説明してるが、どんなゲームにも等しく適用できる訳ではなく、Trueskill実装内部に変化がある訳ではない。