はじめに
AUTOMATIC1111のWeb_UIでの追加機能に追加のサンプリング法などがある。
これを見れば、Web_UIの追加機能のほとんどについては説明されている。
しかし、追加サンプリング法に関してはどのような意味を持つのか分かりにくい。ソースを見て自分なりの注釈を入れたい。
オイラー法とかホイン法と聞いて「ああ、あれね」とすぐ納得できる方には不要である。
Sampling method
AUTOMATIC1111ではサンプリング法としてEuler a, Euler, LMS, Heun, DPM2, DPM2 a, DDIM, PLMSがある。

Samplerのソースを見ると以下の様なコメントがある。
def sample_euler(model, x, sigmas, extra_args=None, callback=None, disable=None, s_churn=0., s_tmin=0., s_tmax=float('inf'), s_noise=1.):
"""Implements Algorithm 2 (Euler steps) from Karras et al. (2022)."""
...
def sample_euler_ancestral(model, x, sigmas, extra_args=None, callback=None, disable=None):
"""Ancestral sampling with Euler method steps."""
...
def sample_heun(model, x, sigmas, extra_args=None, callback=None, disable=None, s_churn=0., s_tmin=0., s_tmax=float('inf'), s_noise=1.):
"""Implements Algorithm 2 (Heun steps) from Karras et al. (2022)."""
...
def sample_dpm_2(model, x, sigmas, extra_args=None, callback=None, disable=None, s_churn=0., s_tmin=0., s_tmax=float('inf'), s_noise=1.):
"""A sampler inspired by DPM-Solver-2 and Algorithm 2 from Karras et al. (2022)."""
...
def sample_dpm_2_ancestral(model, x, sigmas, extra_args=None, callback=None, disable=None):
"""Ancestral sampling with DPM-Solver inspired second-order steps."""
...
def sample_lms(model, x, sigmas, extra_args=None, callback=None, disable=None, order=4):
...
ここでオイラー法とかあるのは常微分方程式の数値解法である。
オイラー法(1次)とホイン法(2次)はそれぞれ1次と2次の誤差の精度である。また有名なルンゲ=クッタ法は4次の誤差の精度である。
y'=f(x, y)\\
y_{n+1}=y_n + hf(x_n, y_n)+O(h^2)
k_1=hf(x_n, y_n)\\
k_2=hf(x_n+\frac{h}{2}, y_n + \frac{k_1}{2})\\
y_{n+1}=y_n + k_2 + O(h^3)
k_1=hf(x_n, y_n)\\
k_2=hf(x_n+h, y_n + k_1)\\
y_{n+1}=y_n + \frac{1}{2}(k_1 +k_2) + O(h^3)
k_1=hf(x_n, y_n)\\
k_2=hf(x_n+\frac{h}{2}, y_n+\frac{k_1}{2})\\
k_3=hf(x_n+\frac{h}{2}, y_n+\frac{k_2}{2})\\
k_4=hf(x_n+h, y_n+k_3)\\
y_{n+1}=y_n+\frac{k_1}{6}+\frac{k_2}{3}+\frac{k_3}{3}+\frac{k_4}{6}+O(h^5)
ちなみにルンゲ=クッタ法を使うのはこの論文でRK4と書いているSamplerである。
DPM2はDPM-Solver-2かと思われる。これは上述の中点法(midpoint method)の一種のように思う。
一方、LMSはlinear_multistep(線型多段法)である。
この論文にはLinear Multi-Step Methodについても書かれてあり、四次では以下。
y_{n+4}=y_{n+3} + h(\frac{55}{24}f'(x_{n+3}, y_{n+3}) - \frac{59}{24}f'(x_{n+2}, y_{n+2})+\frac{37}{24}f'(x_{n+1}, y_{n+1}) - \frac{9}{24}f'(x_n, y_n))\\
PLMSはデフォルト手法だが、上記LMSと関連がある。
ソースを見ると過去の移動量を覚えて使っているように見える。$\frac{55}{24}$など係数はLMSでの係数と一致している。
if len(old_eps) == 0:
# Pseudo Improved Euler (2nd order)
x_prev, pred_x0 = get_x_prev_and_pred_x0(e_t, index)
e_t_next = get_model_output(x_prev, t_next)
e_t_prime = (e_t + e_t_next) / 2
elif len(old_eps) == 1:
# 2nd order Pseudo Linear Multistep (Adams-Bashforth)
e_t_prime = (3 * e_t - old_eps[-1]) / 2
elif len(old_eps) == 2:
# 3nd order Pseudo Linear Multistep (Adams-Bashforth)
e_t_prime = (23 * e_t - 16 * old_eps[-1] + 5 * old_eps[-2]) / 12
elif len(old_eps) >= 3:
# 4nd order Pseudo Linear Multistep (Adams-Bashforth)
e_t_prime = (55 * e_t - 59 * old_eps[-1] + 37 * old_eps[-2] - 9 * old_eps[-3]) / 24
aが付くときAncestral samplingを意味する(参考1、参考2)。詳細は不明。
DPM2とheunは1stepあたりEulerの2倍の回数、拡散モデルを通過するので実行時間が増える。
LMSやPLMSはEulerより高次の計算をするが、過去の拡散モデルの出力を保持するので実行時間は増えない。
Samplerの違いに関して正確な理解がしたいなら常微分方程式の数値解法に関する勉強をすればよい。
euler_samplingのソース
比較的簡単なeuler_samplingのソースを追っかける。
xの現在のノイズ分散を$\sigma[i]$、次のstepにおけるノイズ分散を$\sigma[i+1]$とする。
ここからノイズを加えて$\hat{\sigma}$にして(①)、拡散モデルを通してノイズを加えたxのデノイズ出力を得る(②)。xとdenoisedの差分の勾配を使って$\sigma[i+1]$におけるxを予測する(③)

def to_d(x, sigma, denoised):
"""Converts a denoiser output to a Karras ODE derivative."""
return (x - denoised) / append_dims(sigma, x.ndim)
def euler_sampling(self, ac, x, S, cond, unconditional_conditioning = None, unconditional_guidance_scale = 1,extra_args=None,callback=None, disable=None, s_churn=0., s_tmin=0., s_tmax=float('inf'), s_noise=1.):
"""Implements Algorithm 2 (Euler steps) from Karras et al. (2022)."""
extra_args = {} if extra_args is None else extra_args
cvd = CompVisDenoiser(ac)
sigmas = cvd.get_sigmas(S)
x = x*sigmas[0]
s_in = x.new_ones([x.shape[0]]).half()
for i in trange(len(sigmas) - 1, disable=disable):
gamma = min(s_churn / (len(sigmas) - 1), 2 ** 0.5 - 1) if s_tmin <= sigmas[i] <= s_tmax else 0.
eps = torch.randn_like(x) * s_noise
sigma_hat = (sigmas[i] * (gamma + 1)).half()
if gamma > 0:
x = x + eps * (sigma_hat ** 2 - sigmas[i] ** 2) ** 0.5
s_i = sigma_hat * s_in
x_in = torch.cat([x] * 2)
t_in = torch.cat([s_i] * 2)
cond_in = torch.cat([unconditional_conditioning, cond])
c_out, c_in = [append_dims(tmp, x_in.ndim) for tmp in cvd.get_scalings(t_in)]
eps = self.apply_model(x_in * c_in, cvd.sigma_to_t(t_in), cond_in)
e_t_uncond, e_t = (x_in + eps * c_out).chunk(2)
denoised = e_t_uncond + unconditional_guidance_scale * (e_t - e_t_uncond)
d = to_d(x, sigma_hat, denoised)
if callback is not None:
callback({'x': x, 'i': i, 'sigma': sigmas[i], 'sigma_hat': sigma_hat, 'denoised': denoised})
dt = sigmas[i + 1] - sigma_hat
# Euler method
x = x + d * dt
return x
一方、Ancestral samplingのソースは似ているがノイズを加える手順が異なるような気がする。正直、よく分からないが。
Sampling methodとStepの比較
せっかく、Sampling methodについて言及したのでこの効果の比較をした実験を紹介したい。
デフォルトの手法はPLMSある。頭にk_があるのはk-diffusionの実装。末尾にaがつくとAncestral samplingで作風も変わる。またCFGの大きさにも依存するらしい。
8stepの場合、精度はSampling methodによって違う。 特にデフォルトのPLMSは少ないstepではそれほど良くない。

ただし、DDIMを例にとれば、stepが小さければこのサンプリング法を取ると結果は改善するが、stepが十分大きければ逆にStochansticに及んでいない。(論文)
従ってstepが小さいならSampling methodを変えるメリットはあるが、stepが十分大きいならSampling methodをデフォルトから変えると却ってノイズが増えて悪化する可能性があるので注意する。
Negative prompt
ネガティブプロンプトの名称からマイナスのpromptという印象を受ける。
しかし、ソースを見たところ以下の通りであった。
つまり、通常のpromptがcに対してnegative promptはucに代入される。
通常のstable diffusionにはCFG(classifier free guidance)を計算させるために、ucには「""」という何の意味も示さないpromptが入っているが、これにNegative promptで指定した任意テキストを入れた場合と等しくなる。
class StableDiffusionProcessing:
...
self.negative_prompt: str = (negative_prompt or "")
...
def process_images(p: StableDiffusionProcessing) -> Processed:
...
uc = prompt_parser.get_learned_conditioning(len(prompts) * [p.negative_prompt], p.steps)
c = prompt_parser.get_learned_conditioning(prompts, p.steps)
ネガティブプロンプトは設定したpromptを通常promptから差し引くわけではなく、ucの中に入れられる。従ってネガティブプロンプトを設定すると通常promptが変化するわけではなく、CFG(classifier free guidance)成分が変化する。
例えば
prompt:笑顔、initial seed:無表情、negative prompt:無表情ならCFGは無表情=>笑顔である。
これによって無表情+(無表情から笑顔の変化)なので笑顔になりうる。OK
prompt:笑顔、initial seed:泣き顔、negative prompt:無表情ならCFGは無表情=>笑顔である。
これによって泣き顔+(無表情から笑顔の変化)が必ずしも笑顔にならない。NG
prompt:笑顔、initial seed:泣き顔、negative prompt:泣き顔ならCFGは泣き顔=>笑顔である。
これによって泣き顔+(泣き顔から笑顔の変化)なので笑顔になりうる。OK
従って、negative promptが必要になるには初期latentが意味を持っていてかつそれと同じに揃えられた場合に限られるのではないかと想像する。
StableDiffusionではCFG_Scaleは1が標準
論文などでCFGは以下の様に書かれている。
z_{n+1}=\epsilon(z_n, c) + cfg\_scale\cdot(\epsilon(z_n,c) - \epsilon(z_n,uc))
一方、StableDiffusionでは実装において下記である。
ucの入力の拡散モデルの出力にCFGを足した形になっている。
z_{n+1}=\epsilon(z_n, uc) + cfg\_scale\cdot(\epsilon(z_n,c) - \epsilon(z_n,uc))
これはCFGスケールの上記論文ではデフォルト0なのに対して、実装においてはデフォルト1になっている。
従ってStableDiffusionの実装はCFG_Scaleが論文より1だけ大きくなる。
Attention
promptを()で括ると強調、[]で括ると弱めるという機能が追加されている。
これはソースから以下の該当部分であると思われる。その後、multがどう作用するかは省略。
つまり、(で1.1を掛け、)で1.1で割る。[で1.1で割り、]で1.1を掛ける。という事は(と]は実は同じ記号として作用する。
また、どんなに[]で重みを弱めても重みがマイナスになることはない。マイナスの重みはネガティブプロンプトかと思っていたが違うようなのでどうやって作るのか謎である。
tokens_with_parens = [(k, v) for k, v in self.tokenizer.get_vocab().items() if '(' in k or ')' in k or '[' in k or ']' in k]
for text, ident in tokens_with_parens:
mult = 1.0
for c in text:
if c == '[':
mult /= 1.1
if c == ']':
mult *= 1.1
if c == '(':
mult *= 1.1
if c == ')':
mult /= 1.1
if mult != 1.0:
self.token_mults[ident] = mult
Sampling methodとCFGの考察
現行の拡散モデルは二方向の移動があり、ノイズの多寡(timestep方向)とpromptの忠実性の方向があると解釈できるとする。Sampling methodはtimestep方向、CFGはpromptの忠実性の方向の移動を加速させる。別の言い方では荒いstepでの移動精度を向上させる。
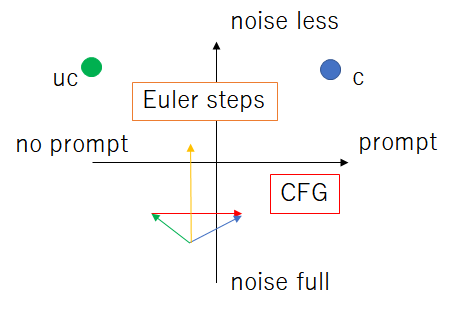
Sampling methodにおけるオイラー法の式と
y_{n+1}=y_n + hf(x_n, y_n)+O(h^2)
CFG(classifier free guidance)が似ているように感じる。
z_{n+1}=\epsilon(z_n, c) + cfg\_scale\cdot(\epsilon(z_n,c) - \epsilon(z_n,uc))
ここでオイラー法はtimestep方向、CFGはpromptの忠実性方向と考えればそれぞれ処理を同時にやっていると見なせるのだろうか。
z_{n+1}=z_n + h(\epsilon(z_n,c)-z_n) + cfg\_scale\cdot(\epsilon(z_n,c) - \epsilon(z_n,uc))
それともそれぞれを交互にやっている感じだろうか。
z_{n+1}=\epsilon(z_{n}, c)+cfg\_scale\cdot(\epsilon(z_{n},c) - \epsilon(z_{n},uc))\\
z_{n+2}=z_n + h(z_{n+1}-z_n)
これはおそらく後者であると思われる。
まとめ
StableDiffusionの追加サンプリング法について自分なりに理解をメモした。
また、StableDiffusionではCFGの大きさが論文での値より1大きい。

