CNNの畳み込みの計算をpythonで実装してみたらim2colになっていた話。
im2colって?
かの有名な「ゼロから作るdeep learning」の畳み込み演算に出てくる関数。(自分はこの本持ってませんが…)検索するとこんなのが出てきます。
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
N, C, H, W = input_data.shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
img2colでも引っ掛かりますが、多分同じ内容です。
単純な畳み込み計算
単純にfor文で畳み込みを計算してみます。
入力$(224,224,8)$を出力$(224,224,16)$に変換するサイズ$(3,3)$の二次元畳み込みを考えるとします。
畳み込みをforループの力業で無理に計算しようとすれば以下のような計算をすればよいことになります。
import numpy as np
import itertools
np.random.seed(100)
# (224,224,8)=>(224,224,16)
input = np.ones((224,224,8))
output = np.zeros((224,224,16))
weight = np.random.random_sample((3,3,8,16))
input = np.pad(input, [(1,1),(1,1),(0,0)], 'constant') # (224,224,8)=>(226,226,8)
x = np.zeros((224,224,8,16))
# case simple conv cal
for ch1, ch2, i, j, k, l in itertools.product(range(8), range(16), range(224), range(224), range(3), range(3)):
x[i,j,ch1,ch2] += input[i+k,j+l,ch1] * weight[k,l,ch1,ch2]
output = np.sum(x, axis=(2))
output1= [[[17.6167424 16.46092477 16.71833326 ... 15.7476869 16.24364858
15.14112872]...
time= 74.62933945655823[s]
単純な式で記述出来ますが、この多重for文では計算に非常に時間がかかります。
この単純な畳み込み計算は現実的ではありません。
一次元畳み込みの場合
最初は簡単な一次元畳み込みを代わりに考えてみます。
ここで$*$は畳み込み演算子です。するとこの式は以下のように記述できます。
この整理した$z_i$の要素はZeroPaddingした$(0,x_1,x_2,...,x_{n},0)$からひとつずつずらしながら取り出す長さ$n$の配列になります。
このようにZeroPaddingした配列をずらして得た配列をあらかじめ用意してやり、これに畳み込みfilter要素を行列計算してやると多重for文よりも高速になります。
\begin{align}
y &= A*x \\
y &= (A_1,A_2,A_3) * (x_1, x_2, x_3, ... x_m, ... ,x_n)\\
&=(A_2x_1+A_3x_2, A_1x_1+A_2x_2+A_3x_3, ... \\
&\qquad A_1x_{m-1}+A_2x_{m}+A_3x_{m+1},...\\
&\qquad A_1x_{n-1}+A_2x_{n} )\\
&=A_1(0,x_1,x_2,...,x_{n-2},x_{n-1})\\
&+A_2(x_1,x_2,x_3...,x_{n-1},x_{n})\\
&+A_3(x_2,x_3,x_4...x_{n},0)\\
&=(A_1,A_2,A_3)\cdot(z_1,z_2,z_3)
\end{align}
二次元の畳み込みの場合もこれと同様に考える事ができます。
実装
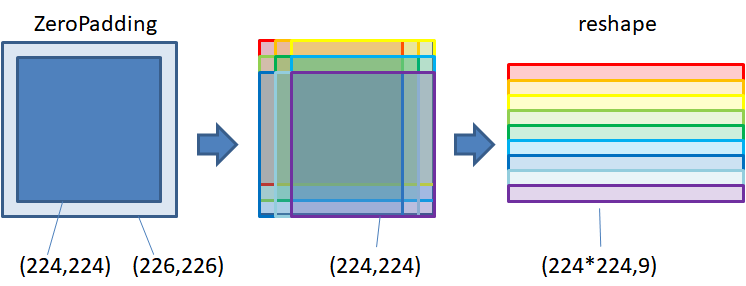
以下はZeroPaddingしたinputをずらしてxの配列を取り、それを変形して重みとの行列積計算を行います。ここでfilter要素数9×入力チャンネル数8=内積計算の長さ$72$になってます。
念のため範囲を全部書けば$(224,224)$をZeroPaddingした$(226,226)$の配列の内$(0:224,0:224),$$(1:225,0:224),$$(2:226,0:224),$$(0:224,1:225),$$(1:225,1:225),$$(2:226,1:225),$$(0:224,2:226),$$(1:225,2:226)$$,(2:226,2:226)$の9通りの範囲になります。
input = np.pad(input, [(1,1),(1,1),(0,0)], 'constant') # (224,224,8)=>(226,226,8)
# case im2col
x = np.zeros((224,224,8,3,3))
weight = weight.transpose((2,0,1,3)) # (3,3,8,16) => (8,3,3,16)
weight = np.reshape(weight,(72,16)) # (8,3,3,16) => (72,16)
for i, j in itertools.product(range(3), range(3)):
x[:,:,:,i,j] = input[i:224+i,j:224+j]
x = np.reshape(x,(224*224,72)) # (224,224,8,3,3) => (224*224,72)
x = np.dot(x,weight) # (224*224,72)*(72,16) => (224*224,16)
output = np.reshape(x,(224,224,16)) # (224*224,16) => (224,224,16)
output2= [[[17.6167424 16.46092477 16.71833326 ... 15.7476869 16.24364858
15.14112872]...
time= 0.0625007152557373[s]
この場合、計算時間はかなり短くなりました。また、計算結果も単純な畳み込み計算結果と合ってます。
ここでこの内容を探してみると前述のim2col関数が引っ掛かりました。
比較してみるとim2col関数にはSample数の次元がありますが、やってることはほとんど同じです。
結局、畳み込み演算も単なる行列積演算なんですね。
備考:
1. 畳み込みフィルターの大きさが(5,5)の場合
input = np.pad(input, [(2,2),(2,2),(0,0)], 'constant') # (224,224,8)=>(228,228,8)
x = np.zeros((224,224,8,5,5))
for i, j in itertools.product(range(5), range(5)):
x[:,:,:,i,j] = input[i:224+i,j:224+j]
2. stridesの大きさが(1,2)の場合
strides = (1,2)
input = np.pad(input, [(1,1),(1,1),(0,0)], 'constant') # (224,224,8)=>(226,226,8)
for i, j in itertools.product(range(3), range(3)):
x[:,:,:,i,j] = input[i:224+i:strides[0],j:224+j:strides[1]]
3. dilated convolutionの場合
input = np.pad(input, [(2,2),(2,2),(0,0)], 'constant') # (224,224,8)=>(228,228,8)
for i, j in itertools.product(range(3), range(3)):
x[:,:,:,i,j] = input[i*2:224+i*2,j*2:224+j*2]