はじめに
深層学習の畳み込み演算において画像サイズを半分にするのによくAveragePooling2DやMaxPooling2Dが使われます。画像サイズを半分にすることで以降の畳み込み層においてフィルタのkernel_sizeが実質的に大きくなります。
一方、Conv2Dにおけるstridesも画像サイズを半分にする目的でたまに使われます。
この違いは畳み込み演算のフィルタ広さにどのように影響を与えうるのか考えてみます。
※注意
畳み込み各層に活性化関数reluが入っている場合、以降議論するように単純な畳み込みに直すことは不可能です。このため以降の議論は活性化関数が存在しない場合のみ成り立つという限定された条件になります。
1. scipy.signalの畳み込み計算
最初にscipy.signal.correlate2d()及び、scipy.signal.convolve2d()を使って二次元畳み込みが計算できることを確認します。適当にA1とB1を定義した場合、良く知るB1にA1を畳み込む結果はcorrelate2d()で得ることが出来ました。またconvolve2d()を使う場合は行列の並びを逆にする必要があるので注意が必要です。
import numpy as np
import scipy.signal as sp
A1 = np.random.randint(0,2,(3,3))
B1 = np.random.randint(-4,5,(7,7))
C1 = sp.correlate2d(B1, A1, mode='valid')
C2 = sp.convolve2d(B1, A1[::-1,::-1], mode='valid')
print('A1=\n', A1)
print('B1=\n', B1)
print('C1=\n', C1)
print('C2=\n', C2)
-----------------------------------------------
A1=
[[0 1 0]
[0 0 0]
[1 0 1]]
B1=
[[-1 -3 4 -3 1 -2 -2]
[-3 -4 -2 -2 1 3 2]
[-1 -4 2 3 3 3 -3]
[ 3 -3 -2 1 3 -1 0]
[ 2 -4 0 2 4 0 2]
[ 4 0 -3 4 4 3 0]
[ 0 -4 -2 4 3 -3 1]]
C1=
[[-2 3 2 7 -2]
[-3 -4 -1 1 6]
[-2 0 7 5 9]
[-2 2 2 10 3]
[-6 0 3 5 4]]
C2=
[[-2 3 2 7 -2]
[-3 -4 -1 1 6]
[-2 0 7 5 9]
[-2 2 2 10 3]
[-6 0 3 5 4]]
2. 3x3畳み込みが2回掛けられる場合
Kerasの記述において以下のように3x3畳み込みが2回掛けられる場合、どのような畳み込み演算と等価でしょうか。これは多くの人が知っているように5x5畳み込み1回と等価になります。(※ただし畳み込みの間に活性化関数reluがないという条件下です)
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
以下のようにB1にA1=>A2を畳み込んだ結果C1と、A1とA2の畳み込みを求めた結果D1で畳み込む結果E1は同じになることが示せます。従って3x3畳み込みが2回は5x5畳み込み1回と等しく、
その5x5畳み込みフィルタはD1 = sp.convolve2d(A1, A2, mode='full')で計算できます。
import numpy as np
import scipy.signal as sp
A1 = np.random.randint(0,2,(3,3))
A2 = np.random.randint(0,2,(3,3))
B1 = np.random.randint(-4,5,(7,7))
C1 = sp.correlate2d(B1, A1, mode='valid')
C2 = sp.correlate2d(C1, A2, mode='valid')
D1 = sp.convolve2d(A1, A2, mode='full')
E1 = sp.correlate2d(B1, D1, mode='valid')
print('A1=\n', A1)
print('A2=\n', A2)
print('B1=\n', B1)
print('C1=\n', C1)
print('C2=\n', C2)
print('D1=\n', D1)
print('E1=\n', E1)
----------------------------------------------
A1=
[[1 0 1]
[1 1 1]
[0 0 0]]
A2=
[[0 0 1]
[0 1 0]
[0 0 0]]
B1=
[[-3 -4 4 -4 0 -2 3]
[ 2 0 -3 3 4 2 -4]
[ 0 4 -4 0 1 1 2]
[-4 -3 0 -1 -3 0 -2]
[ 4 1 2 -2 -3 -1 1]
[ 3 -1 -1 -4 -1 3 -2]
[ 4 0 -1 -3 -4 -4 -3]]
C1=
[[ 0 -8 8 3 5]
[ -1 3 -2 7 4]
[-11 0 -7 -3 -2]
[ 3 -3 -6 -7 -8]
[ 7 -7 -7 -5 -2]]
C2=
[[ 11 1 12]
[ -2 0 1]
[-10 -9 -9]]
D1=
[[0 0 1 0 1]
[0 1 1 2 1]
[0 1 1 1 0]
[0 0 0 0 0]
[0 0 0 0 0]]
E1=
[[ 11 1 12]
[ -2 0 1]
[-10 -9 -9]]
3. 5x5畳み込みが1回掛けられる場合
2.とは逆の事を考えてみましょう。任意の5x5畳み込み1回存在しているとき、これを2回の3x3畳み込みに分解することは可能でしょうか?理論的には任意の5x5畳み込み1回と3x3畳み込み1回の畳み込みフィルタが明らかであるのならば、もう一個の3x3畳み込みの重みは逆畳み込みを計算すればいいことになります。
D1 = convolve2d(A1, A2)ならばA2 = deconvolve2d(D1, A1)である。
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (5, 5), padding="valid")(x)
しかし、二次元の逆畳み込みの関数はscipyでは存在しないのでscipyでは確認できませんでした。
画像用の逆畳み込みの関数を使うと以下のようにF1,F2において逆畳み込みの近似値が得られました。
そもそも論でいえば任意の5x5畳み込みのパラメータ数は25に対して、3x3畳み込み2回のパラメータ数は18なのですべての5x5畳み込みを3x3畳み込み2回で示すのはパラメータ数的に不可能です。
import numpy as np
import scipy.signal as sp
from skimage import restoration
A1 = np.random.randint(0,2,(3,3))
A2 = np.random.randint(0,2,(3,3))
D1 = sp.convolve2d(A1, A2, mode='full')
F1, _ = restoration.unsupervised_wiener(D1, A2)
F2, _ = restoration.unsupervised_wiener(D1, A1)
print('A1=\n', A1)
print('A2=\n', A2)
print('D1=\n', D1)
print('F1=\n', F1[1:-1,1:-1])
print('F2=\n', F2[1:-1,1:-1])
---------------------------------
A1=
[[1 1 0]
[1 0 0]
[0 1 1]]
A2=
[[0 0 0]
[1 1 1]
[0 0 0]]
D1=
[[0 0 0 0 0]
[1 2 2 1 0]
[1 1 1 0 0]
[0 1 2 2 1]
[0 0 0 0 0]]
F1=
[[ 0.96529897 0.89627574 0.13951081]
[ 0.7975316 0.15137364 -0.02074955]
[ 0.0798071 0.92025068 0.92801951]]
F2=
[[ 0.00971747 0.0117676 0.00229734]
[ 0.96429178 0.99937217 0.97182209]
[-0.00158553 0.03361686 -0.00815724]]
まとめると
・任意の3x3畳み込み2回は5x5畳み込み1回に変換可能である=>真
・任意の5x5畳み込み1回は3x3畳み込み2回に変換可能である=>偽(近似値なら可能)
4. AveragePooling((2,2))の場合
さて、プールサイズが(2,2)のAveragePoolingは
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)で畳み込みフィルタの重みが((0.25,0.25),(0.25,0.25))であるConv2Dの演算に等しいことを示したい。
以下のように平滑フィルタA1を定義すれば、B1にA1を畳み込んでstrides処理をした結果D2はAveragePoolingの結果C1と等しい。
x = Input(shape=(28, 28, 1))
x = AveragePooling2D((2, 2))(x)
import numpy as np
import scipy.signal as sp
import skimage.measure
A1 = np.ones((2,2))/4
B1 = np.random.randint(-4,5,(8,8))*4
C1 = skimage.measure.block_reduce(B1, (2,2), np.average)
D1 = sp.correlate2d(B1, A1, mode='valid')
D2 = D1[::2,::2]
print('A1=\n', A1)
print('B1=\n', B1)
print('C1=\n', C1)
print('D1=\n', D1)
print('D2=\n', D2)
---------------------------------
A1=
[[0.25 0.25]
[0.25 0.25]]
B1=
[[-12 -4 0 8 -4 4 -12 -8]
[ 4 -4 8 -12 -8 -16 -12 -8]
[-16 -16 -16 8 8 -16 -12 0]
[-12 -8 -4 16 -4 -8 -16 -4]
[-12 -8 -12 16 -4 4 -4 0]
[-12 -12 4 -8 -12 8 0 16]
[ -8 16 8 16 -12 -12 -16 0]
[ -8 4 4 -12 12 -4 -16 4]]
C1=
[[ -4. 1. -6. -10.]
[-13. 1. -5. -8.]
[-11. 0. -1. 3.]
[ 1. 4. -4. -7.]]
D1=
[[ -4. 0. 1. -4. -6. -9. -10.]
[ -8. -7. -3. -1. -8. -14. -8.]
[-13. -11. 1. 7. -5. -13. -8.]
[-10. -8. 4. 6. -3. -6. -6.]
[-11. -7. 0. -2. -1. 2. 3.]
[ -4. 4. 5. -4. -7. -5. 0.]
[ 1. 8. 4. 1. -4. -12. -7.]]
D2=
[[ -4. 1. -6. -10.]
[-13. 1. -5. -8.]
[-11. 0. -1. 3.]
[ 1. 4. -4. -7.]]
従ってAveragePoolingは以下に等しい。ただし、フィルタの値は平滑フィルタである。
x = Input(shape=(28, 28, 1))
x = AveragePooling2D((2, 2))(x)
---------------------------------
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
5. Conv2D+AveragePooling((2,2))の場合
以下のようにConv2DとAveragePoolingがある場合、これを単純な畳み込みに直してみたい。
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = AveragePooling2D((2,2))(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
この時、AveragePooling後の3x3の畳み込みA2フィルタ処理はAveragePoolingを無くして考えると、同じ値で埋めた2倍の大きさの6x6畳み込みフィルタA3を畳み込んでからstridesを掛けた結果に等しいことが分かる。
A2:
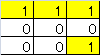
A3:
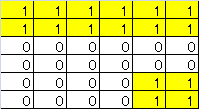
以下、C3とE2が等しいのが確認できる。
import numpy as np
import scipy.signal as sp
import skimage.measure
A1 = np.random.randint(0,2,(3,3))
A2 = np.random.randint(0,2,(3,3))
A3 = np.repeat(A2, 2, axis=0)
A3 = np.repeat(A3, 2, axis=1)
B1 = np.random.randint(-4,5,(12,12))
C1 = sp.correlate2d(B1, A1, mode='valid')
C2 = skimage.measure.block_reduce(C1, (2,2), np.average)
C3 = sp.correlate2d(C2, A2, mode='valid')
D1 = sp.convolve2d(A1, A3, mode='full')
E1 = sp.correlate2d(B1, D1, mode='valid')/4
E2 = E1[::2,::2]
print('A1=\n', A1)
print('A2=\n', A2)
print('A3=\n', A3)
print('B1=\n', B1)
print('C1=\n', C1)
print('C2=\n', C2)
print('C3=\n', C3)
print('D1=\n', D1)
print('E1=\n', E1)
print('E2=\n', E2)
------------------------------
A1=
[[0 0 1]
[1 0 0]
[0 0 1]]
A2=
[[1 1 1]
[0 0 0]
[0 0 1]]
A3=
[[1 1 1 1 1 1]
[1 1 1 1 1 1]
[0 0 0 0 0 0]
[0 0 0 0 0 0]
[0 0 0 0 1 1]
[0 0 0 0 1 1]]
B1=
[[ 0 -2 -1 -3 -4 2 -3 -1 -3 -4 -2 1]
[ 4 -1 2 -4 -4 4 -1 -1 -4 -2 2 2]
[ 1 -4 3 3 -2 2 3 -2 -3 4 -1 2]
[-3 -1 -4 4 0 3 1 0 0 0 -4 1]
[ 3 1 4 1 -2 -2 2 1 -3 0 3 -3]
[-4 0 3 -4 3 4 2 0 3 0 1 -4]
[ 1 -3 -1 -1 3 -4 -2 3 -4 1 0 -3]
[ 1 -4 0 4 4 3 -2 -4 3 -2 3 0]
[ 0 2 -2 3 3 3 2 -2 -1 0 1 -1]
[-4 -4 2 -2 -4 -1 4 4 -1 3 -1 4]
[ 4 4 -2 -1 -1 0 4 -2 3 3 -4 4]
[-4 -3 0 -1 -2 0 -2 3 3 -1 -2 -4]]
C1=
[[ 6 -1 -4 0 -4 1 -7 -1 -7 1]
[ -1 -4 -1 10 -2 1 -1 -4 -5 7]
[ 4 3 -8 4 5 2 -5 4 2 -1]
[ 2 1 7 8 1 -2 5 1 -6 -3]
[ -1 0 4 -10 3 8 -5 1 6 -6]
[ 4 -3 6 6 3 -8 4 1 0 -3]
[ -2 -2 6 3 4 4 -7 -3 4 -6]
[ 2 4 -2 5 5 3 4 -1 1 4]
[ -8 -2 4 1 2 -5 6 7 -4 6]
[ 6 1 -8 -2 1 7 6 0 0 3]]
C2=
[[ 0. 1.25 -1. -3.25 -1. ]
[ 2.5 2.75 1.5 1.25 -2. ]
[ 0. 1.5 1.5 0.25 -0.75]
[ 0.5 3. 4. -1.75 0.75]
[-0.75 -1.25 1.25 4.75 1.25]]
C3=
[[ 1.75 -2.75 -6. ]
[10.75 3.75 1.5 ]
[ 4.25 8. 2.25]]
D1=
[[0 0 1 1 1 1 1 1]
[1 1 2 2 2 2 1 1]
[1 1 2 2 2 2 1 1]
[0 0 1 1 1 1 1 1]
[0 0 0 0 0 0 1 1]
[0 0 0 0 1 1 1 1]
[0 0 0 0 1 1 1 1]
[0 0 0 0 0 0 1 1]]
E1=
[[ 1.75 -3.25 -2.75 -2.75 -6. ]
[ 4. -0.75 0. 3.25 -0.5 ]
[10.75 6.25 3.75 5. 1.5 ]
[ 6.5 7. 9.25 3.25 2.5 ]
[ 4.25 5.5 8. 3. 2.25]]
E2=
[[ 1.75 -2.75 -6. ]
[10.75 3.75 1.5 ]
[ 4.25 8. 2.25]]
すなわちは下記のConv2DとAveragePoolingからなるモデルは以下のように整理可能である。
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = AveragePooling2D((2,2))(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
-----------------------------------------
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (6, 6), padding="valid", strides=2)(x)
-----------------------------------------
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (8, 8), padding="valid", strides=2)(x)
6. Conv2D+AveragePooling((2,2))の場合2
以下のようにConv2DとAveragePoolingがある場合、これを単純な畳み込みに直してみたい。
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = AveragePooling2D((2,2))(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = AveragePooling2D((2,2))(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
これは以下のように計算可能です。
Conv2DとAveragePoolingを掛けた結果のC5が6x6でstrides2を二回掛けたE3結果と等しいことが分かります。
import numpy as np
import scipy.signal as sp
import skimage.measure
A1 = np.random.randint(0,2,(3,3))
A2 = np.random.randint(0,2,(3,3))
A3 = np.random.randint(0,2,(3,3))
A4 = np.repeat(A2, 2, axis=0)
A4 = np.repeat(A4, 2, axis=1)
A5 = np.repeat(A3, 2, axis=0)
A5 = np.repeat(A5, 2, axis=1)
B1 = np.random.randint(-4,5,(26,26))*4
C1 = sp.correlate2d(B1, A1, mode='valid')
C2 = skimage.measure.block_reduce(C1, (2,2), np.average)
C3 = sp.correlate2d(C2, A2, mode='valid')
C4 = skimage.measure.block_reduce(C3, (2,2), np.average)
C5 = sp.correlate2d(C4, A3, mode='valid')
D1 = sp.convolve2d(A1, A4, mode='full')
E1 = sp.correlate2d(B1, D1, mode='valid')/4
E2 = E1[::2,::2]
E3 = sp.correlate2d(E2, A5, mode='valid')/4
E3 = E3[::2,::2]
print('A1=\n', A1)
print('A2=\n', A2)
print('A3=\n', A3)
print('A4=\n', A4)
print('A5=\n', A5)
print('C5=\n', C5)
print('E3=\n', E3)
--------------------------
A1=
[[1 1 0]
[1 0 0]
[0 0 0]]
A2=
[[0 0 0]
[0 0 0]
[1 1 0]]
A3=
[[1 0 1]
[0 0 1]
[1 0 1]]
A4=
[[0 0 0 0 0 0]
[0 0 0 0 0 0]
[0 0 0 0 0 0]
[0 0 0 0 0 0]
[1 1 1 1 0 0]
[1 1 1 1 0 0]]
A5=
[[1 1 0 0 1 1]
[1 1 0 0 1 1]
[0 0 0 0 1 1]
[0 0 0 0 1 1]
[1 1 0 0 1 1]
[1 1 0 0 1 1]]
C5=
[[ -6.75 -15.5 -45.5 ]
[-32.5 1.25 9.75]
[-15.5 5.75 -28. ]]
E3=
[[ -6.75 -15.5 -45.5 ]
[-32.5 1.25 9.75]
[-15.5 5.75 -28. ]]
すなわちは下記のConv2DとAveragePoolingからなるモデルは以下のように整理可能である。
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = AveragePooling2D((2,2))(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = AveragePooling2D((2,2))(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
-----------------------------------------
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (6, 6), padding="valid", strides=2)(x)
x = Conv2D(1, (6, 6), padding="valid", strides=2)(x)
さて、等価な式として整理するには上記までが限界である。
しかし、近似値を許し3.に示すように逆畳み込みにより畳み込みを分解することを許可すれば、上記式はもう少し整理できる。2x2の平滑フィルタの逆畳み込みによって5x5畳み込みフィルタを求めれば
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (6, 6), padding="valid", strides=2)(x)
x = Conv2D(1, (6, 6), padding="valid", strides=2)(x)
-----------------------------------------
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x) # AveragePooling2D((2,2))
x = Conv2D(1, (6, 6), padding="valid")(x)
x = Conv2D(1, (1, 1), padding="valid", strides=2)(x)
-----------------------------------------
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (12, 12), padding="valid", strides=2)(x)
x = Conv2D(1, (1, 1), padding="valid", strides=2)(x)
-----------------------------------------
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (9, 9), padding="valid")(x)
x = Conv2D(1, (4, 4), padding="valid", strides=4)(x)
-----------------------------------------
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (9, 9), padding="valid")(x)
x = AveragePooling2D((4,4))(x)
ここで5x5の畳み込みフィルタは3x3の畳み込みフィルタを同じ値で埋めた6x6の畳み込みフィルタから2x2の平滑フィルタの逆畳み込みで求めた畳み込みフィルタ。
9x9の畳み込みフィルタは3x3の畳み込みフィルタを同じ値で4倍埋めた12x12の畳み込みフィルタから4x4の平滑フィルタの逆畳み込みで求めた畳み込みフィルタである。
すなわち畳み込みをまとめれば以下の様である。
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (18, 18), padding="valid", strides=4)(x)
-----------------------------------------
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (15, 15), padding="valid")(x)
x = AveragePooling2D((4,4))(x)
7. Conv2D+strides=2の場合
以下の様なstrideが入るモデルを考える。
これは6.のように3x3の畳み込みが3回、画像サイズの半減が2回入っているという意味では近い。
また、計算に用いられるパラメータ数も3x3フィルタが3個なので重みの数的にも同じである。
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (3, 3), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
3.のように畳み込みを分解することを許可するとすれば
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
-----------------------------------------
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (4, 4), padding="valid", strides=2)(x)
x = Conv2D(1, (6, 6), padding="valid", strides=2)(x)
-----------------------------------------
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (6, 6), padding="valid", strides=2)(x)
-----------------------------------------
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (12, 12), padding="valid", strides=4)(x)
-----------------------------------------
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (9, 9), padding="valid")(x)
x = Conv2D(1, (4, 4), padding="valid", strides=4)(x)
-----------------------------------------
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (9, 9), padding="valid")(x)
x = AveragePooling2D((4,4))(x)
となり6.と比較すると畳み込みフィルタの大きさは若干小さいことが分かる。
もしAveragePooling2Dと同じ畳み込みフィルタの大きさにするにはstridesを使う場合のフィルタサイズを1大きくする必要があるのではないかと思います。
x = Input(shape=(28, 28, 1))
x = Conv2D(1, (4, 4), padding="valid", strides=2)(x)
x = Conv2D(1, (4, 4), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
8. 更に多段モデルの場合
- AveragePooling2Dの場合
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = AveragePooling2D((2,2))(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = AveragePooling2D((2,2))(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = AveragePooling2D((2,2))(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = AveragePooling2D((2,2))(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
平滑フィルタの逆畳み込みによって畳み込みの分解を許せば、
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (6, 6), padding="valid", strides=2)(x)
x = Conv2D(1, (6, 6), padding="valid", strides=2)(x)
x = Conv2D(1, (6, 6), padding="valid", strides=2)(x)
x = Conv2D(1, (6, 6), padding="valid", strides=2)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (6, 6), padding="valid")(x)
x = Conv2D(1, (1, 1), padding="valid", strides=2)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (10, 10), padding="valid", strides=2)(x)
x = Conv2D(1, (10, 10), padding="valid", strides=2)(x)
x = Conv2D(1, (12, 12), padding="valid", strides=2)(x)
x = Conv2D(1, (1, 1), padding="valid", strides=2)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (9, 9), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (9, 9), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (12, 12), padding="valid")(x)
x = Conv2D(1, (1, 1), padding="valid", strides=4)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (9, 9), padding="valid")(x)
x = Conv2D(1, (18, 18), padding="valid", strides=2)(x)
x = Conv2D(1, (24, 24), padding="valid", strides=2)(x)
x = Conv2D(1, (1, 1), padding="valid", strides=4)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (9, 9), padding="valid")(x)
x = Conv2D(1, (17, 17), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (24, 24), padding="valid")(x)
x = Conv2D(1, (1, 1), padding="valid", strides=8)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (9, 9), padding="valid")(x)
x = Conv2D(1, (17, 17), padding="valid")(x)
x = Conv2D(1, (48, 48), padding="valid", strides=2)(x)
x = Conv2D(1, (1, 1), padding="valid", strides=8)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (9, 9), padding="valid")(x)
x = Conv2D(1, (17, 17), padding="valid")(x)
x = Conv2D(1, (33, 33), padding="valid")(x)
x = Conv2D(1, (16, 16), padding="valid", strides=16)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (63, 63), padding="valid")(x)
x = AveragePooling2D((16,16))(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (78, 78), padding="valid", strides=16)(x)
となり各層の畳み込みの大きさはAveragePooling2Dを経るたびに**(3→5→9→17→33)**と大きくなるのが分かります。要するに各層の畳み込みの大きさは倍々に増えていきます。
- Conv2D+strides=2の場合
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (3, 3), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
平滑フィルタの逆畳み込みによって畳み込みの分解を許せば、
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (4, 4), padding="valid", strides=2)(x)
x = Conv2D(1, (4, 4), padding="valid", strides=2)(x)
x = Conv2D(1, (4, 4), padding="valid", strides=2)(x)
x = Conv2D(1, (6, 6), padding="valid", strides=2)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (6, 6), padding="valid")(x)
x = Conv2D(1, (1, 1), padding="valid", strides=2)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (6, 6), padding="valid", strides=2)(x)
x = Conv2D(1, (6, 6), padding="valid", strides=2)(x)
x = Conv2D(1, (12, 12), padding="valid", strides=2)(x)
x = Conv2D(1, (1, 1), padding="valid", strides=2)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (12, 12), padding="valid")(x)
x = Conv2D(1, (1, 1), padding="valid", strides=4)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (10, 10), padding="valid", strides=2)(x)
x = Conv2D(1, (24, 24), padding="valid", strides=2)(x)
x = Conv2D(1, (1, 1), padding="valid", strides=4)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (9, 9), padding="valid")(x)
x = Conv2D(1, (2, 2), padding="valid", strides=2)(x)
x = Conv2D(1, (24, 24), padding="valid")(x)
x = Conv2D(1, (1, 1), padding="valid", strides=8)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (9, 9), padding="valid")(x)
x = Conv2D(1, (48, 48), padding="valid", strides=2)(x)
x = Conv2D(1, (1, 1), padding="valid", strides=8)(x)
-----------------------------------------
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (2, 2), padding="valid")(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
x = Conv2D(1, (5, 5), padding="valid")(x)
x = Conv2D(1, (9, 9), padding="valid")(x)
x = Conv2D(1, (33, 33), padding="valid")(x)
x = Conv2D(1, (16, 16), padding="valid", strides=16)(x)
-----------------------------------------
となり各層の畳み込みの大きさはstrides=2を経るたびに**(2→3→5→9→33)**と大きくなるのが分かります。
AveragePoolingと比較すると、最終層の畳み込み大きさだけアンバランスに思えます。
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (3, 3), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid", strides=2)(x)
x = Conv2D(1, (2, 2), padding="valid")(x)
最終畳み込みのサイズを2x2にすれば畳み込みの大きさは**(2→3→5→9→17)**となります。
しかし、2x2畳み込みは高速化に寄与しないので特に用いる意味はありません。
x = Input(shape=(224, 224, 1))
x = Conv2D(1, (4, 4), padding="valid", strides=2)(x)
x = Conv2D(1, (4, 4), padding="valid", strides=2)(x)
x = Conv2D(1, (4, 4), padding="valid", strides=2)(x)
x = Conv2D(1, (4, 4), padding="valid", strides=2)(x)
x = Conv2D(1, (3, 3), padding="valid")(x)
また、上記のように4x4畳み込みを用いればAveragePoolingと同様の**(3→5→9→17→33)**を再現できます。
これはAveragePoolingの2x2の平滑フィルタを逆畳み込みを演算する分、Conv2D+strides=2ではフィルタの大きさが1小さくなることを示唆します。
Conv2D+strides=2で4x4のフィルタを考えるならば、AveragePoolingよりもパラメータ数が多くなるデメリットがあります。(逆に言えばメリットなのかもしれませんが)
このような様々な大きさの畳み込みフィルタを使って任意サイズの特徴量の抽出を行う畳み込みフィルタを生成可能か考えるのは有限個の分銅で連続的な重さを計る問題を思い出します。
まとめ:
Conv2DのstridesとAveragePoolingを使った場合の畳み込みフィルタの大きさを考察しました。
どちらも画像サイズを半分にする処理ですがConv2Dのstridesを使った場合、AveragePoolingよりも畳み込みフィルタの大きさが小さくなることが示唆されました。
尤も、このような整理が可能なのは活性化関数reluがない場合、逆畳み込みによって畳み込みが二つに分解できる場合に限られますので、一般のモデルにおいてこのような整理は出来ませんので注意が必要です。