活性化関数のトレンドとして最近SwishやMishが有名です。
Geluに関して説明している日本語の記事がないので自分なりの理解をまとめたいと思います。
これに関する説明がおそらくSwishの理解につながると思われます。
論文:https://arxiv.org/abs/1606.08415
Gelu定義
Gelu = x \Phi (x) = x * \frac{1}{2}[1+erf(\frac{x}{\sqrt{2}})]
Geluは以上のように定義されます。
ここで$\Phi (x)$は正規分布(ガウス分布)の累積分布関数です。$erf()$は誤差関数です。
これが理想的な関数ですが一般に誤差関数は初等関数で計算できないので近似が行われます。
\begin{align}
Gelu &= 0.5x(1+tanh[\sqrt{\frac{2}{\pi}}(x+0.044715x^3)])\\
Gelu &= x\sigma (1.702x)\\
Swish &= x\sigma (\beta x)\\
\end{align}
このGelu、およびGeluの近似をプロットしてみて、relu関数との差分を考えてみます。
ここでGelu idealとGelu approximate 1は大体等しいです。
一方、Gelu approximate 2はGelu idealと若干誤差があることが分かります。
ここで$\beta = 1.702$のSwish関数はGelu approximate 2と等価であることが分かります。
従ってGeluが有利である理由を掴めれば、それがSwishが有利な理由になります。
なお、この論文中ではβ=1のSwish関数はSiLUと呼称しています。
ただし$\beta = 1.702$のSwish関数とGelu approximate 2と等しいとはいえ、厳密なGelu関数はSwish関数とは異なることに注意する必要があります。
import matplotlib.pyplot as plt
import numpy as np
from scipy import special
x = np.arange(-6, 6, 0.05)
y1 = np.array([i if i>0 else 0 for i in x]) # Relu
y2 = x*0.5*(1+special.erf(np.sqrt(0.5)*x)) # Gelu ideal
y3 = x*0.5*(1+np.tanh(np.sqrt(2/np.pi)*(x+0.044715*x*x*x))) # Gelu approximate 1
y4 = x/(1+np.exp(-1.702*x)) # Gelu approximate 2
plt.plot(x, y1, label="Relu")
plt.plot(x, y2, label="Gelu ideal")
plt.plot(x, y3, label="Gelu approximate 1")
plt.plot(x, y4, label="Gelu approximate 2")
plt.legend()
plt.show()
plt.plot(x, y2-y1, label="Gelu ideal - Relu")
plt.plot(x, y3-y1, label="Gelu approximate 1 - Relu")
plt.plot(x, y4-y1, label="Gelu approximate 2 - Relu")
plt.legend()
plt.show()
Geluが有利である理由の推測
Gelu-Reluのグラフにもう一度注目します。この時Gelu-Reluは二つの谷があるグラフになります。そして勾配が0になるのは$x=±1$付近です。またGeluはGAUSSIAN ERROR LINEAR UNITSの略です。
以上から推測を行うと、この活性化関数は関数の入力を1か-1に近づける勾配成分を持つのではないかと思われます。(いわゆる正則化を推進する項が活性化関数に含まれる)

activity_regularizer(中間層の出力に関する正則化)のL1,L2正則化との比較を考えてみたい。この場合の追加する損失関数成分は$\lambda |x|, \lambda x^2$である。
この損失関数を加えると出力はどの値でもゼロの方向に近づくが、出力が小さくなりすぎると逆に追加の損失関数よりも本来の損失関数が増大するので、出力の大きさは結局どこかで釣り合うようになる。
Gelu-Reluの差分を追加の損失関数と見なせば出力がゼロに近すぎるとき、逆にこの関数は出力を大きくしようとする成分を持つ。これはactivity_regularizerのL1,L2正則化にはない項である。

Mishとの比較
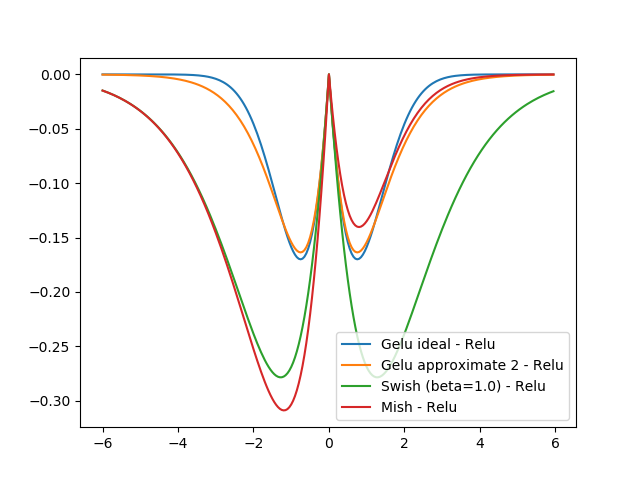
Geluと$\beta = 1$のSwishとMishのReluの差分を比べたところ以下の通りでした。
Mishは正と負で谷の大きさと場所が異なります。
Mishは負の領域で$\beta = 1.0$のSwishに近いですが、正の領域でGelu approximate 2($\beta = 1.702$のSwish)に近い気がします。
(ついでに何故、Mishが負の領域の方に偏っている理由を妄想しますと、負の値の収束値を大きくした方が正則化した際に正の値を取る入力の割合が大きくなるからとか考えました。)
y5 = x/(1+np.exp(-1.0*x)) # Swish (beta=1.0)
y6 = x*np.tanh(np.log(1+np.exp(x))) # Mish
plt.plot(x, y2-y1, label="Gelu ideal - Relu")
plt.plot(x, y4-y1, label="Gelu approximate 2 - Relu")
plt.plot(x, y5-y1, label="Swish (beta=1.0) - Relu")
plt.plot(x, y6-y1, label="Mish - Relu")
plt.legend()
plt.show()
まとめ:
GeluをRelu関数からの変分成分を表示させた。
Relu関数からの変分という解釈でプロットする記事が見当たらないので良い解釈かどうか分からないが、この場合Geluは入力を1か-1に近づける勾配成分を持つ、というのが自分の理解である。
これはMish論文にself regularized(自己正則化)という単語で現れるがそれではないかと思います。
