波動に渦に！極座標移動による回転拡縮シェーダーを作ってみた

本記事はサムザップ Advent Calendar 2017の24日目の記事です。

はじめに

新卒3年目のエンジニアで、二宮といいます。
シャドウバースが好きで、プレミアムカードの仕組みとかをいろいろ妄想していたのですが、
春にこちらの講演を聞いて、いてもたってもいられず発表されたシャドウバースのプレミアムカードの演出を再現しちゃいました。
この記事では、その時に作成したものの中から、波動や渦などの表現に使える「回転と拡縮を同時に行う機能」を紹介しようと思います。

つくったもの

とりあえず、作ったサンプルを載せますね。
回転と拡縮を行っているものになります。

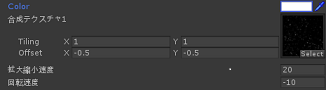
Materialでの設定はこちら。上記サンプルのためにいじっているのは拡大縮小速度、回転速度だけ。

元素材はこちら

かいせつ～

それでは、どうやって実現したかの解説をします！

っていうか、この記事、タイトルでやることほぼわかってしまうんですが、、、ｗ
一言でいうとこの機能は「画像に極座標フィルタをかけて表示する機能」です。

（あ、もし「きょくざひょう」ってなに、、、？ってなった人は軽く調べてくださいね。仮に良くわからなくても、xyの代わりに原点からの距離と回転角で座標を表現するんだな。ってわかれば大丈夫です。）

機能の実現方法をざっくり説明します。
バーテックスシェーダは普通で、フラグメントシェーダーのところだけをいじっています。

フラグメントシェーダの処理内容としては、

1. UV値を極座標変換し、r, θを求める
2. r, θに対し、_Timeを使って、スクロールをかける
3. (u, v)の代わりに、(r, θ)を使って画素値のサンプリングを行う

ということをしています。

画像へのアクセス自体を (u, v) ではなく、極座標系の値 (r, θ) を使って行います。
このため、画像自体は、極座標系で扱われる画像として生成しなければなりません。

Shaderコードとしては、こんな感じ。

half3 frag(vertexOutput input) : COLOR
{
	half2 uv = input.uvTex;
	uv = ConvertPolarCordinate(uv, _RSpeed, _ThetaSpeed); // 直交座標のUV値を、極座標系の拡縮回転スクロール後の値にコンバート！
	return tex2D(_Tex, uv).a * _Color; // 極座標系の値でテクスチャの画素データをサンプリング
}

順を追ってもう少し詳しく見ていきます。

画像の生成

極座標系で扱われる画像ってどうつくんの、、、？
ってなる人のためにまずは、画像の生成方法についてちょっと触れます。

一旦、このシェーダーで通常の画像を表示した場合を見てみましょう。
極座標変換されて表示されることになるので、だいぶ見た目が変わります。

素材

Shaderで表示

どこがどうなったか分かりました、、？
ちゃんとそれっぽい絵を出したければ、この変換の逆算をした絵を使う必要があります。

とははえ、横軸がrで、縦軸がθだから、、、とかって考えるのは難しいし、、。
そこで、PhotoShopさんの極座標フィルタを使います。極座標=>直交座標への変換をかけた画像を使います。

極座標フィルタによる変換後画像素材

Shaderで表示

うん、まぁちょっとぶれたけど、、、だいたい書いた通り。
と、こんな感じでひと手間をかけるとか、想像力働かせるとかして、極座標で扱われる前提の画像を使う必要があります。

UV値の変換

さてさて、極座標(r, θ)によるアクセスが可能な画像の準備ができたところで、UVの極座標変換＋拡大縮小操作について書いていきます！

ここでやっていることはとっても単純です。
通常の直交座標のUV値を極座標のrθに変換後、通常のUVスクロールでやるように、_Timeをつかってrθをいじればよいだけです。

というわけで、コードのせます

half2 ConvertPolarCordinate(half2 uv, half rSpeed, half thetaSpeed) {
	const half PI2THETA = 1 / (3.1415926535 * 2);
	half2 res;

	// UV値を極座標系に変換
	uv = 2 * uv - 1;
	half r = 1 - sqrt(uv.x * uv.x + uv.y * uv.y);
	half theta = atan2(uv.y, uv.x) * PI2THETA + 0.75; //　0.75はPhotoShopの変換に合わせた、回転の始軸の調整

	// スクロールのための処理
	res.y = r + rSpeed * _Time;
	res.x = theta + thetaSpeed * _Time;
	return res;
}

こんな感じです。

UV値の極座標系への変換では、

1. UVを単位円と同じように扱えるように、UVの値域を0 ~ 1 から -1 ~ 1に変換
2. 単位円における極座標系への変換
   を行っています。

スクロール処理は、通常のUVスクロールと同じですね。
以上、説明でした。

さいごに

ここまで読んでくださったみなさま、ありがとうございました。
極座標移動による回転拡縮シェーダー、いかがでしたでしょうか。
何かの役に立てれば嬉しいです。

さ、明日は @kida_hironari さんのハッカソン事前準備で作ったハッカソン向け基盤システムです！
最近ハッカソンで受賞しって聞いたし楽しみにしてます！！
よろしくおねがいしまーす。

おまけ

サンプルのコード全部載せときますね。

使うときには、テクスチャのαチャンネルを読むようにしているので、注意してください。
それから、Tilingをいじると楕円になったり、Offsetをいじると回転の中心をずらしたりもできるので、いろいろ試してみてください～。

Shader "PolarScroll" 
{
	Properties
	{
		_Color("Color", Color) = (1,1,1,1)
		_Tex("合成テクスチャ1", 2D) = "black" {}
		_RSpeed("拡大縮小速度", Float) = 0
		_ThetaSpeed("回転速度", Float) = 0
	}

	SubShader
	{
		BlendOp Add
		Blend One Zero
		Cull Back
		Lighting Off
		ZWrite On
		ZTest LEqual
		Fog{ Mode Off }

		Tags{ "Queue" = "Geometry" "IgnoreProjector" = "True" "RenderType" = "Opaque" }
		Pass{
		CGPROGRAM

#pragma vertex vert
#pragma fragment frag

			uniform sampler2D _Tex;
			uniform half4 _Tex_ST;
			uniform half3 _Color;
			uniform half _RSpeed;
			uniform half _ThetaSpeed;

			struct vertexInput {
				half4 vertex : POSITION;
				half2 uv : TEXCOORD0;
			};

			struct vertexOutput {
				half4 pos : SV_POSITION;
				half2 uvTex : TEXCOORD2;
			};

			vertexOutput vert(vertexInput input)
			{
				vertexOutput output;
				output.pos = UnityObjectToClipPos(input.vertex);
				output.uvTex = input.uv.xy * _Tex_ST.xy + _Tex_ST.zw;
				return output;
			}

			half3 AddWithMaskAlpha(half3 src, half3 dest, half alpha)
			{
				half3 addColor = src * alpha;
				dest.r = dest.r + addColor.r;
				dest.g = dest.g + addColor.g;
				dest.b = dest.b + addColor.b;
				return dest.rgb;
			}

			half2 ConvertPolarCordinate(half2 uv, half rSpeed, half thetaSpeed) {
				const half PI2THETA = 1 / (3.1415926535 * 2);
				half2 res;

				// UV値を極座標系に変換
				uv = 2 * uv - 1;
				half r = 1 - sqrt(uv.x * uv.x + uv.y * uv.y);
				half theta = atan2(uv.y, uv.x) * PI2THETA + 0.75; //　0.75はPhotoShopの変換に合わせた、回転の始軸の調整

				// スクロールのための処理
				res.y = r + rSpeed * _Time;
				res.x = theta + thetaSpeed * _Time;
				return res;
			}

			half3 frag(vertexOutput input) : COLOR
			{
				half2 uv = input.uvTex;
				uv = ConvertPolarCordinate(uv, _RSpeed, _ThetaSpeed);
				return tex2D(_Tex, uv).a * _Color;
			}

		ENDCG
		}
	}
}