CVPR2019(Oral)に採択されたAdaCos: Adaptively Scaling Cosine Logits for Effectively Learning Deep Face Representationsを読んだので記録を残します。
図と表は論文から引用しています。
間違い等お気づきの点ありましたらコメントいただけると幸いです。
事前知識
昨今話題のmetric learningの手法です。metric learningについてはこちらが非常にわかりやすくまとめてくださっているのでそちらを参考にしてください。
概要
ArcFaceやCosFaceといった距離学習には手動で決めるハイパーパラメータがあり、これが実験の結果に大きく影響を与えます。”Ada”という言葉が入っているので察しがつくと思いますが、この論文はそのハイパーパラメータを自動で決定しようというものです。
cosine based softmax lossesのハイパーパラメータの調査
まずは調査からです。これらの距離学習をしたときに、正解クラスとの距離や、正解でないクラスとの距離はどのような変化をするのでしょうか。
$\vec{x_i}$を$i$番目の特徴量、$y_i$を正解ラベル、$N$をバッチサイズとします。$i$番目の特徴量がクラス$j$である確率$P_{i, j}$はsoftmax関数で、
P_{i,j} = \frac{e^{f_{i,j}}}{\sum^{C}_{k=1}e^{f_{i,k}}} \tag{1}
となります。ここで$f_{i,j}$はlogitで、softmax関数のインプットとなります。$C$はクラス数です。このときのクロスエントロピーロスは
L_{CE}=-\frac{1}{N}\sum^{N}_{i=1}\log{P_{i, y_i}} = -\frac{1}{N}\sum^{N}_{i=1}\log{\frac{e^{f_{i,y_i}}}{\sum^{C}_{k=1}e^{f_{i,k}}}}\tag{2}
となります。ArcFaceなどの距離学習ではこの$f_{i,j}$の計算が普通のものと少し違い、$\vec{x_i}$と重み$\vec{W_j}$との内積、つまり$f_{i,j}=\vec{W_{j}}^\mathsf{T}\vec{x_i}$となります。
このとき、$\vec{W}^\mathsf{T}$と$\vec{x_i}$は正規化されているので$f_{i,j}$はコサイン距離$\cos\theta_{i, j}$となります。ここでArcFaceとCosFaceを確認します。
ArcFaceは
f_{i,j}= s\cdot \cos(\theta_{i,j} + \mathbb{1}\{j=y_i\}\cdot m)\tag{3}
CosFaceは
f_{i,j}= s\cdot(\cos\theta_{i,j} + \mathbb{1}\{j=y_i\}\cdot m)\tag{4}
という形をしています。ここで出てくる$m$はマージンパラメータ、$s$はスケールパラメータで、$\mathbb{1}\{j=y_i\}$は$j=y_i$のとき$1$、それ以外が$0$となる関数です。つまり、正解クラスのときだけ$m$だけずれることになり、それだけのズレを許容できるよう学習しなければなりません。それに対して、スケールパラメータ$s$は結果を0と1によりはっきりと分ける、大きい値を強調する働きがあります。
まずはこの$s$と$m$の2つのハイパーパラメータが予測にどのような影響を与えるのか、それぞれ調査していきます。
スケールパラメータs
直感的に学習中、$P_{i,y_i}$は$0$から徐々に$1$に変化していきます。つまり正解となす角$\theta_{i, y_i}$は$\frac{\pi}{2}$から$0$に減少していきます。
[](それでは$P_{i,j}$の値域はどうなっているでしょうか?
最悪ケースは正解クラスとなす角が大きく($cos\theta_{i, y_i}=0$)、それ以外となす角が小さいとき($cos\theta_{i,k \neq y_i}=1$)、つまり\
\frac{e^{s\cdot \cos\theta_{i,y_i}}}{\sum^{C}_{k=1}e^{s\cdot \cos \theta_{i,k}}} = \frac{e^{0}}{\sum^{C-1}_{k \neq y_i}e^{s} + e^{0}} = \frac{1}{1 + (C-1)\cdot e^s} \tag{5}\
```\
です。なお、正解以外となす角を$\theta_{i,k \neq y_i}$としています。\
逆に最も良いときは、正解クラスとなす角が小さく($cos\theta_{i, y_i}=1$)、それ以外となす角が大きいとき($cos\theta_{i,k \neq y_i}=0$)、つまり\
```math\
\frac{e^{s\cdot \cos\theta_{i,y_i}}}{\sum^{C}_{k=1}e^{s\cdot \cos \theta_{i,k}}} = \frac{e^{s}}{\sum^{C-1}_{k \neq y_i}e^{0} + e^{s}} = \frac{e^s}{e^s + (C-1)} \tag{6}\
```\
です。よってcosine basedの$P_{i,j}$の値域は\
```math\frac{1}{1 + (C-1)\cdot e^s} \leq P_{i,j} \leq \frac{e^s}{e^s + (C-1)}```\
となります。sを無限大にとばすと\
```math\lim_{x \to \infty}\left( \frac{e^s}{e^s + (C-1)} - \frac{1}{1 + (C-1)\cdot e^s} \right) = 1 \tag{7}```\
となり、$P_{i,j}$がスケールパラメータsにより、0と1にしっかりと分かれることがわかります。)
$s$の影響を調べるために$P_{i,y_i}$を$s$と$\theta_{i,y_i}$の関数として考えてみます。
```math
P_{i,y_i} = \frac{e^{f^{i,y_i}}}{e^{f^{i,y_i}} + B_i} = \frac{e^{s\cdot \cos\theta_{i,y_i}}}{e^{s\cdot \cos\theta_{i,y_i}} + B_i} \tag{8}
ここで$B_i=\Sigma_{k\neq y_i}e^{f_{i,k}}=\sum_{k\neq y_i}e^{s\cdot\cos\theta_{i,k}}$、つまり正解ラベル以外とのlogitの合計です。
正解ラベル以外となす角$\theta_{i,k\neq y_{i,y_i}}$が学習中にどういった変化をするか調べた結果が下の図1になります。

見てわかるとおり$\theta_{i,k\neq y_i}$はほぼ不変で、ずっと$\pi/2$に張り付いているのが確認できます。
なので$B_i\approx\sum_{i\neq k}e^{s\cdot \cos \frac{\pi}{2}}=C-1$と近似しても問題なさそうです。
再度スケールパラメータ$s$について調べていきます。
$s$を変化させて、$P_{i,y_i}$と$\theta_{i,y_i}$の変化を調べたのが図2(a)です。

クラス数が多く、sが小さすぎるときは$\theta_{i,y_i}$が0のときでも$P_{i,y_i}$は1になりません(どれだけ良く識別していてもペナルティを負うことになります)。逆に$s$が非常に大きいときは、これはこれで問題で、全く明後日の方向を向いていても高い確率を与えます。
マージンパラメータm
ArcFaceのマージンパラメータ$m$に注目します。ArcFaceは$\cos$の中に$m$が入るので、$P_{i,y_i}$は
P_{i,y_i} = \frac{e^{f^{i,y_i}}}{e^{f^{i,y_i}} + B_i} = \frac{e^{s\cdot \cos(\theta_{i,y_i} + m)}}{e^{s\cdot \cos(\theta_{i,y_i} + m)} + B_i} \tag{9}
となります。ここでも同様に$s$と$B_i$を固定し、$m$を変化させて$P_{i,y_i}$と$\theta_{i,y_i}$の変化を確認します(図2(b))。$m$が大きくなると曲線は左に移動します。つまり$m$を大きくすると、$\theta_{i,y_i}$が同じでも、$P_{i,y_i}$は小さくなり、lossが大きくなります。そのため正しい識別とみなすには$\theta_{i,y_i}$が非常に小さくないといけません。$m$が大きすぎれば$P_{i,y_i}$はほとんど$0$になってしまいます。そうすると今度は非常に角が小さいにもかかわらず、lossが大きくなり学習がうまくいきません。
The cosine-based softmax loss with adaptive scaling
解析結果から$s$と$m$は大きすぎても小さすぎても学習がうまくいかないことがわかりました。2つのパラメータがありますが、予測に与える影響は似ているのでパラメータを一つに絞ります。ここでは$s$に絞ってチューニングをしていきます。つまり
P_{i,j} = \frac{e^{\tilde s\cdot \cos\theta_{i,j}}}{\sum^{C}_{k=1}e^{\tilde s\cdot \cos\theta_{i,k}}} \tag{10}
として、この$\tilde s$をヒューリスティックではなく自動で決定することを考えていきます。
再度$P_{i,y_i}$を$\theta_{i,y_i}$の関数として考えます。
[]($\theta_{i,y_i}$は正解ラベルの重みと入力$\vec x_i$がなす角ですが、)
学習の目的は$\theta_{i,y_i}$を損失関数$L_{CE}$を通して小さくすることですが、そのためには$P_{i,y_i}$を大きく変化させる適切な$\tilde s$を選択する必要があります。数学的には$\left | \frac{\partial P_{i, y_i}(\theta)}{\partial\theta} \right |$が最大になる、つまり現在のネットワークの正解となす角を$\theta_0 \in [0, \frac{\pi}{2}]$としたときに
\frac{\partial^{2}P_{i,y_i}(\theta_0)}{\partial{\theta_0^2}}=0 \tag{11}
となる$s_0$を見つけることです。途中計算を省きますが、具体的には
s_0 = \frac{log(B_i)}{cos\theta_0} \tag{12}
となります。ここで$B_i=\sum_{k \neq y_i}e^{s\cdot\cos\theta_{i,k}}\approx C-1$と近似しています。これで、学習に最適なスケールパラメータを求めるには$\theta_0$を考えるだけで良くなりました。
では$\theta_0$をどうするか。$\theta_0$の値域は$[0, \frac{\pi}{2}]$なので、中央である$\frac{\pi}{4}$とすると最適なスケールパラメータ$\tilde{s}_f$は
\tilde s_f=\frac{log(B_i)}{cos{\frac{\pi}{4}}}=\frac{\log\sum_{k\neq y_i}e^s\cdot\cos\theta_{i,k}}{\cos\frac{\pi}{4}}
\approx \sqrt2 \cdot \log(C-1) \tag{13}
となり、このパラメータはクラス数から求められます。
この固定の$\tilde s_f$はクラス数にのみ依存するのでArcFaceなどに対しても利用できます。
これがFixed AdaCosとなります。
Dynamically adaptive scale parameter
図1を見ると正解ラベル以外となす角はだいたい$\frac{\pi}{2}$で安定しますが、$\theta_{i,y_i}$は学習が進むに連れ$0$に近づいていきます。
$\tilde s_f$は固定なので、$\theta_{i, y_j}$が小さくなるに連れスケールパラメータによる監視が弱くなっていきます。そこで、学習の進行具合に合わせて変化する$\tilde s_d$を考えます。
そのためにtイテレーション目のネットワークがミニバッチのそれぞれが正解となす角の中央値$\theta_{med}^{(t)}$を導入します。
[](この$\theta_{med}^{(t)}$は現在のネットワークの大雑把なミニバッチの各正解ラベルとなす角の最適値の代表値といえます。
$\theta_{med}$が大きい場合、ネットワークはまだ学習の途中なので、強い監視をするべきではありません。
逆に$\theta_{med}$が小さい時はネットワークは最適解に近いので、学習の進行具合に合わせた、より強い監視をかけることで更にネットワークの精度を高められるはずです。)
この$\theta_{med}^{(t)}$は学習の進行具合といえます。$\theta_{med}$が大きい場合は学習途中なので弱い監視が、小さい場合はより強い監視が必要です。
そこで、$\tilde s_f$のときは$\theta_0=\frac{\pi}{4}$と決め打ちしていましたが、$\theta_0 = \theta_{med}^{(t)}$とすれば条件に合ったいい感じの監視になりそうです。
また、$\tilde s_f$のときは$B_i= \sqrt 2 \cdot \log(C-1)$と近似し固定していましたが、より正確にするために、$t$イテレーション目での$B_{ave}^{(t)}$を導入します。$B_{ave}^{(t)}$は$B^{(t)}_i$と$\tilde {s}_d^{(t-1)}$用いて、
B_{ave}^{(t)}=\frac{1}{N}\sum_{i \in \mathcal{N}^{(t)}}B_i^{(t)}=\frac{1}{N}\sum_{i \in \mathcal{N}^{(t)}} \sum_{k\neq y_i} e^{\tilde s_d^{(t-1)} \cdot \cos\theta_{i,k}} \tag{14}
とします。$\mathcal{N}^{(t)}$は$t$イテレーション目のミニバッチです。$\theta_{med}^{(t)}$と$B_{ave}^{(t)}$、そして式(12)から
\tilde s_d^{(t)}=\frac{\log{B^{(t)}_{ave}}}{\cos\theta_{med}^{(t)}} \tag{15}
を得ます。また、学習のはじめのときは当然$\theta_{med}^{(t)}$は非常に大きいので、強い監視はしないように、$\theta_{med}^{(t)}$か$\frac{\pi}{4}$のより小さい方を採用します。また$t=0$のときは先程の$\tilde s_f$を使います。
まとめると
\tilde s_d = \left\{
\begin{array}{ll}
\sqrt 2 \cdot \log(C-1) & (t = 0) \\
\frac{\log{B^{(t)}_{ave}}}{\cos(\min(\frac{\pi}{4},\theta_{med}^{(t)}))} & (t \ge 1) \tag{16}
\end{array}
\right.
となります。誤差伝播のときは、$s$を定数として計算するだけです。これがDynamic AdaCosとなります。
以上が提案手法です。
実験
LFW、MegaFace 1-million Challenge、 IJB-C の3つの顔識別のデータセットで性能を比較します。データセットの内容、実験の環境等は割愛させていただきます。気になる方は論文をどうぞ。
Results on LFW
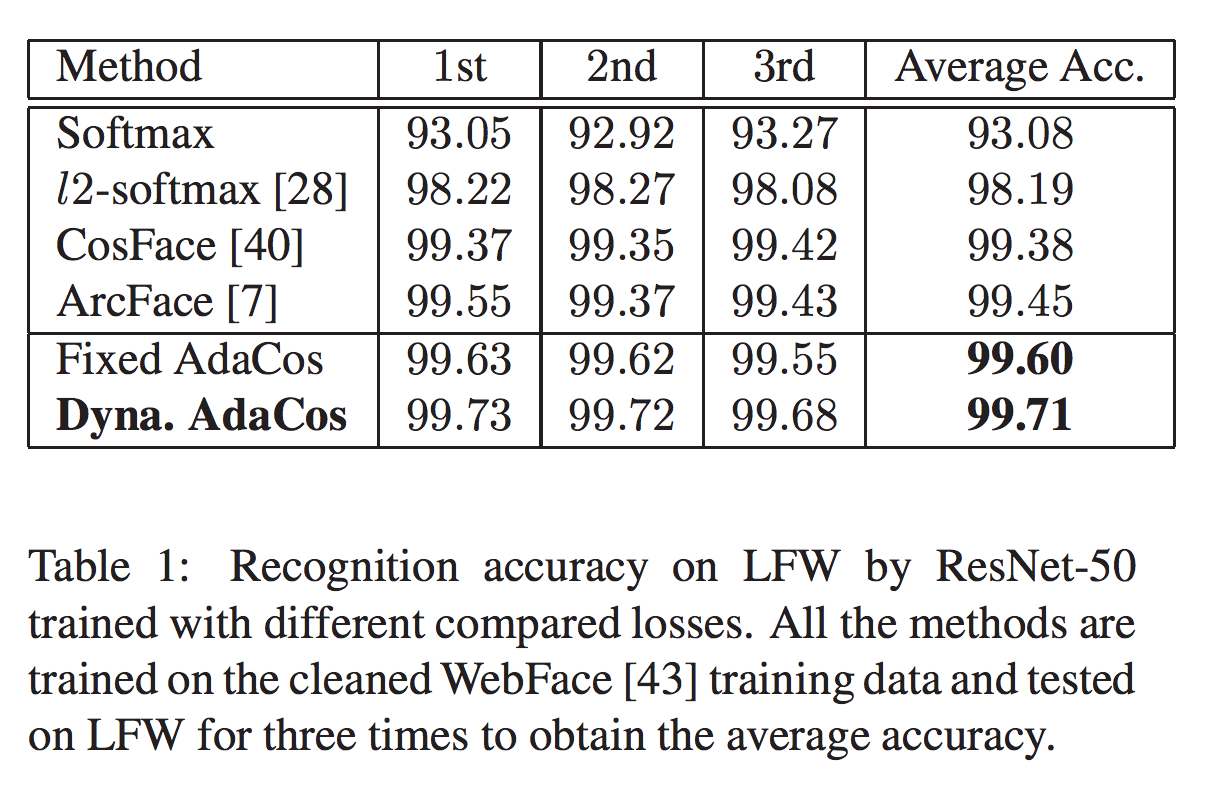
表1がResNet-50を用いたAdaCosと、各cosine basedなモデルとの比較ですが、
Dynamic AdaCosはもちろんのこと、Fixed AdaCosも高いスコアを示しています。LFWは比較的かんたんなので3回の学習とテストをした平均だそうです。
Exploratory Experiments
WebFaceデータセットで学習した際の$\theta_{i,y_i}$と$\tilde{s}$の変化も見ておきます。図3は学習中の$\tilde s$の変化をグラフにしたものです。Fixed AdaCosは固定なので当然横ばいですが、Dynamic AdaCosは徐々に減少し、学習が進むに連れより強い監視をしているのが確認できます。

図4は各手法の$\theta_{i,y_i}$とDynamic AdaCosの$\theta_{i, k \neq y_i}$の推移ですが、AdaCosは他の手法よりも収束が早いのが確認できます。また、正解ラベル以外となす角は$\frac{\pi}{2}$付近を保っています。

Results on MegaFace and IJB-C
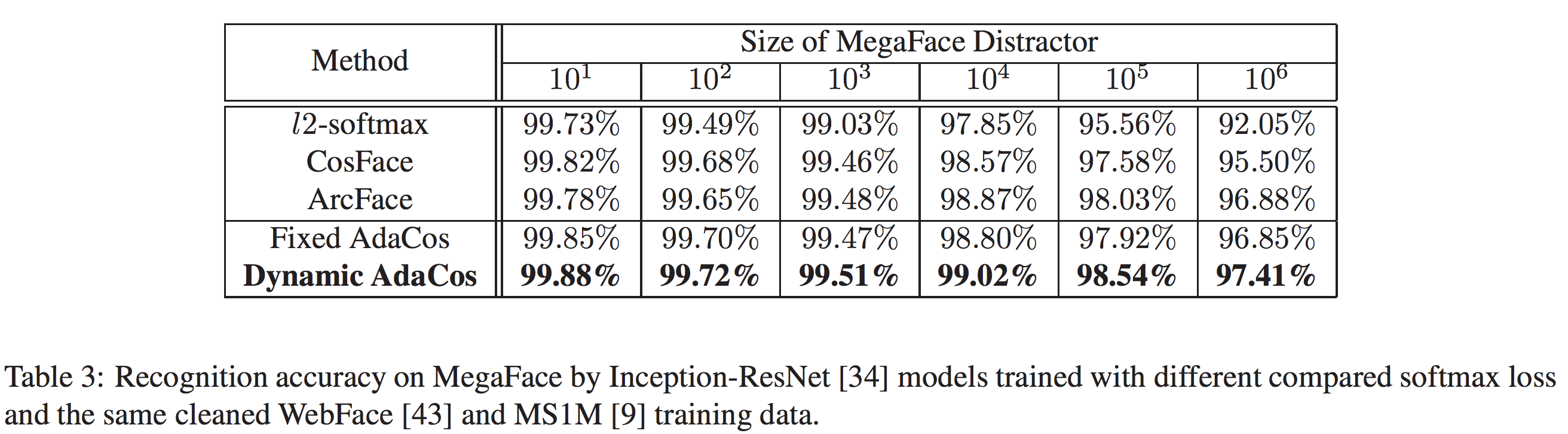
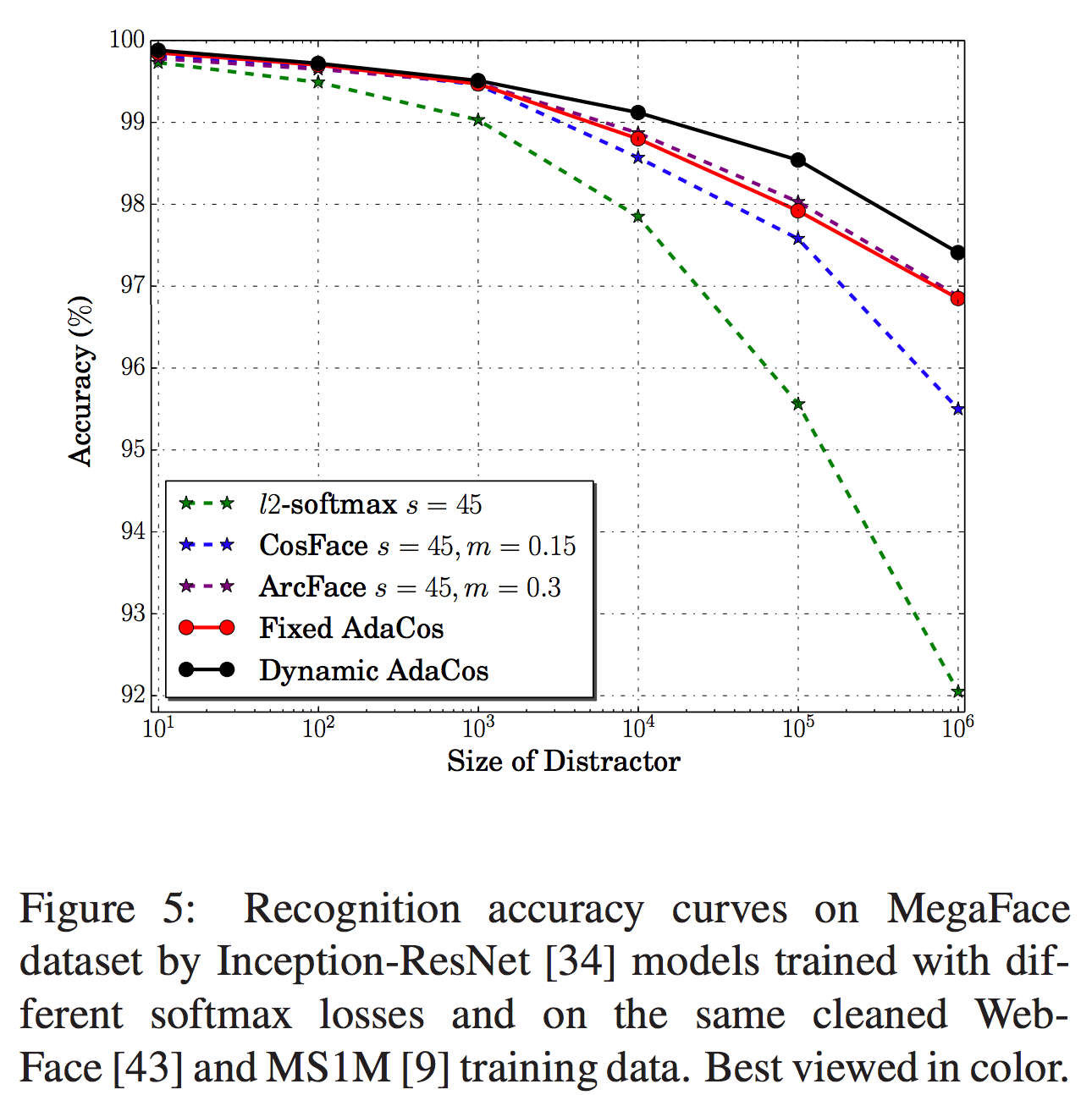
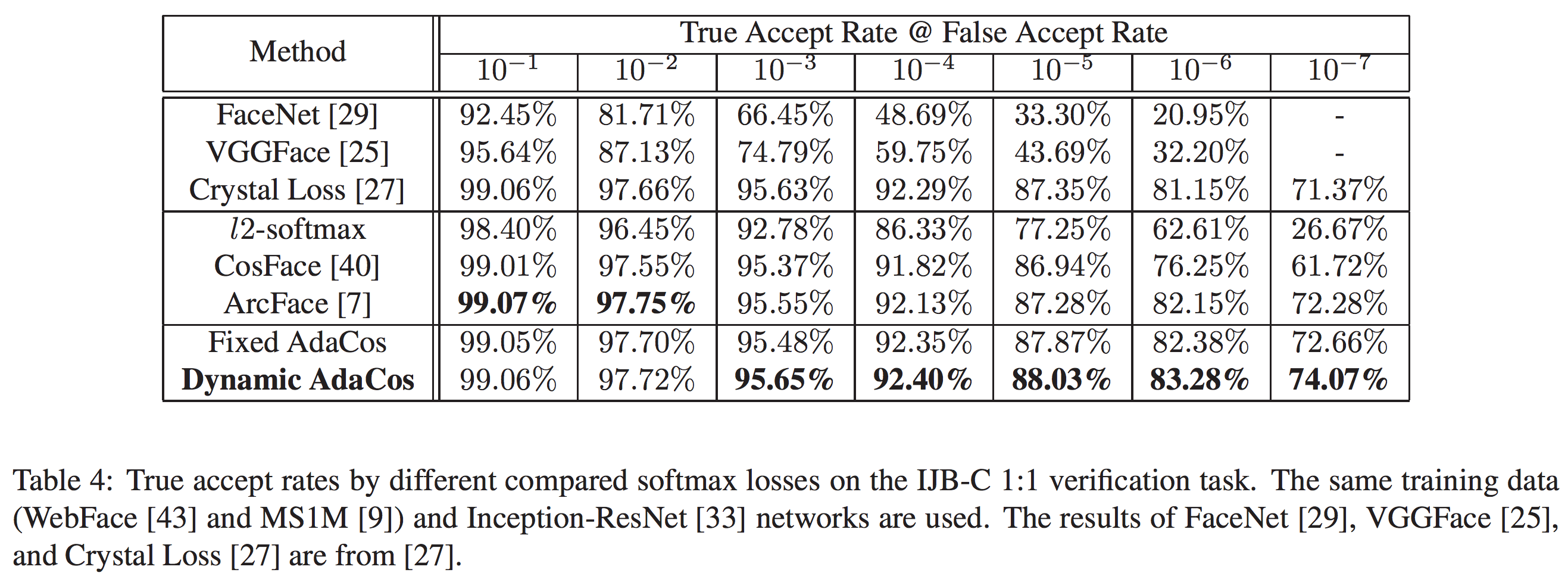
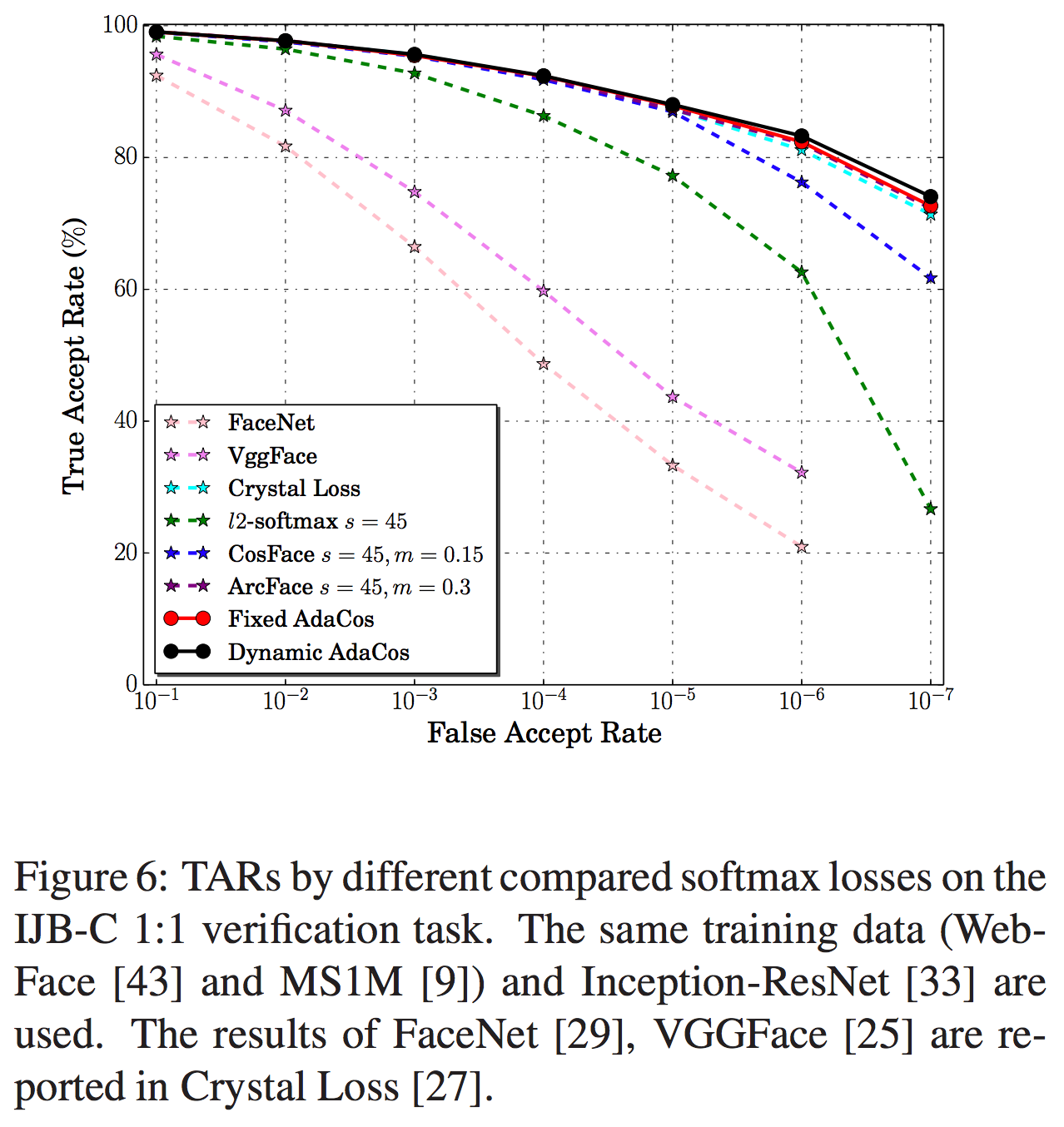
MegaFaceの結果は表3と図5、IJB-Cの結果は表4と図6の通りです。いずれの手法もほぼ既存手法を上回る結果となっています。
実装
こちらの方がpytorchで実装しています。chainerでの実装もほとんど変更なくできるでしょう。ただ、chainerにはmedianがなかったので、cupyで計算することになりますが、$s$の計算課程は必要ないので問題ないでしょう。また、AdaCosは訓練のときに$\theta_{med}$の計算に正解ラベルを使用するので注意してください。
感想
自分はArcFaceを使っており、ArcFaceも非常に優秀だったのですがAdaCosが出てからはこちらを使っています。ハイパーパラメータを設定しなくていいのはもちろんのこと、精度も改善されるので非常におすすめできる手法です。上記のpytorch実装もネットワークの最終層を少し書き換えるだけで導入でき、計算コストも気になりません。ぜひ使ってみてください。