AAAI2020(Oral)に採択されたSoftmax Dissection: Towards Understanding Intra- and Inter-class Objective for Embedding Learning を読んだ(聞いていた)ので今更ながら記録を残します。
図と表は論文から引用しています。
間違い等お気づきの点ありましたらコメントいただけると幸いです。
概要
クラス分類や空間埋め込みなどでは目的関数としてsoftmax関数がよく使われます。これらの目的はintra-class objective(同一クラスのサンプル間距離を小さくする)とinter-class objetive(異なるクラスのサンプル間距離を大きくする)がありますがsoftmax関数はこの2つの目的が絡み合った形をしています。
この論文ではsoftmax関数を分析し、これら2つの目的をきれいに分離したD-Softmaxを提案します。
Introduction
顔認識などでdeep metric learningが注目されてますが、最も単純な方法としてsoftmax lossを使用するものがあります。顔認識なら人数分のクラスを用意し、同じ人の顔は同じクラスに分類するといった感じです。
しかしsoftmax lossには2つの問題があります。
1. intra-class objectives と inter-class objectivesが絡み合っている
図1(a)(b)はそれぞれMS-Celeb-M1からサンプル数が多い5人、10人を選んで特徴量を3次元に圧縮してプロットしたものになります。
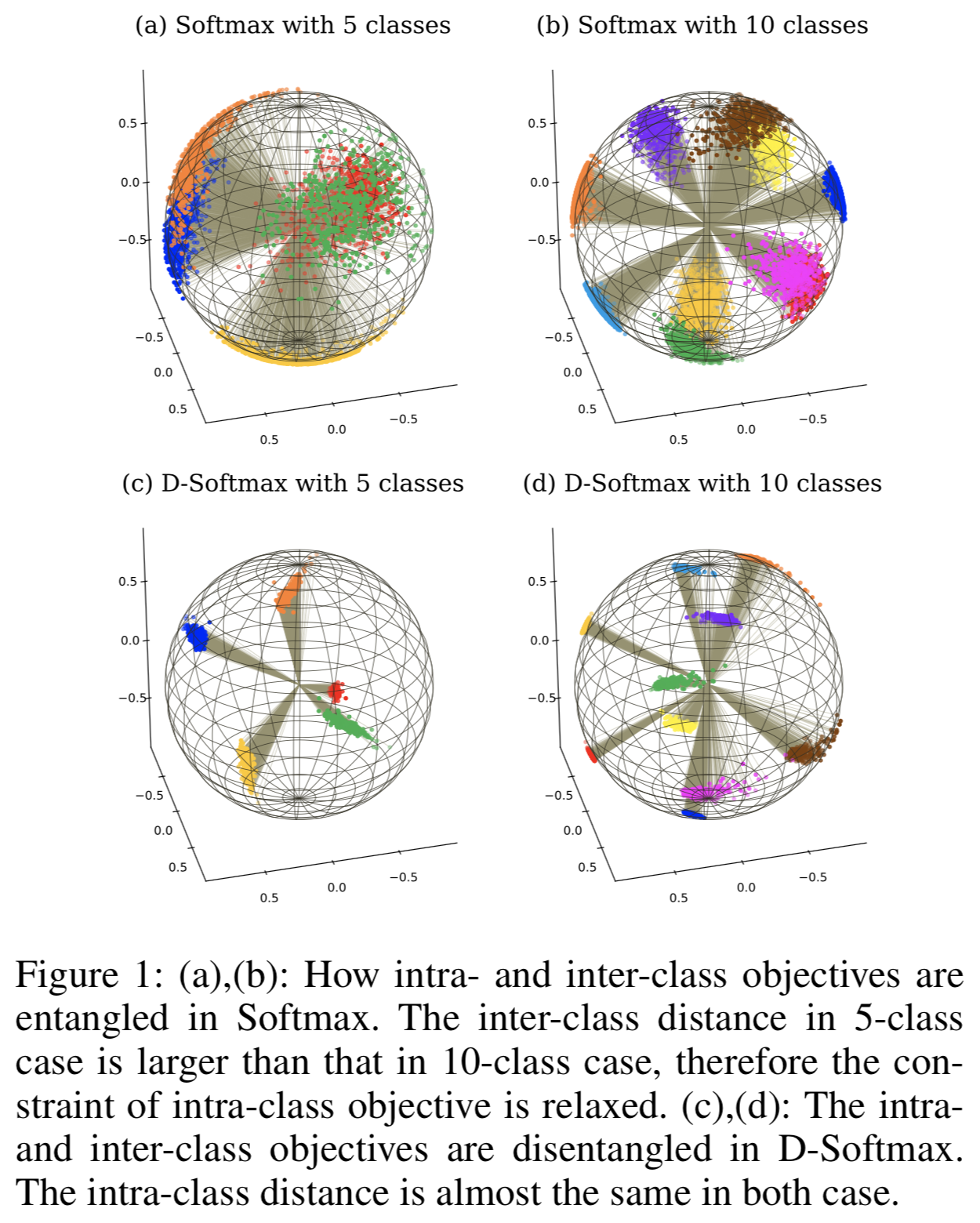
inter-class distanceは大きいですが、intra-class distanceも大きいのがわかります。
これはinter-class distanceが大きくなるにつれintra-class objectiveが弱くなっていくからです。
既存手法ではこの問題に対して目的関数を追加したりArcFaceなどに見られるanglur marginを追加したりすることで対処しています。
2.時間とメモリのコストがかかる
softmaxの計算には全クラスの出力を使用するので、クラス数に線形の時間とメモリを消費します。近年ではクラス数が$10^6$個とかもありえますが、GPUのメモリ上限等を考えると厳しい制約になります。contrastive lossやtriplet lossを使うという手もありますが性能的にsoftmaxに劣ります。
そこでsoftmax lossをintra-class objectiveとinter-class objectiveに分離します。またその結果、それぞれの目的の最適化に、毎回全てのクラスについて計算が必要ではないことがわかりました。
Softmax Dissection
ここからsoftmax cross entropy lossを解剖し、intra-class objectiveとinter-class objectiveに分離していきます。
Preliminary Knowledge
softmax cross entropy lossは
L_s=-\log(\frac{e^{sz_y}}{\sum^K_{k=1}e^{sz_k}}) = \log(1 + \frac{\sum^K_{k \neq y}e^{sz_k}}{e^{sz_y}})
といった形をしています。ここで$s$はスケールパラメータ、$K$はクラス数、$z_k$は$k \in \{ 1, 2,...,K\}$番目のクラスの出力値、$z_y$は正解クラスの出力値です。
一般的にsoftmaxは$z_k=\boldsymbol{w}^\intercal_k \boldsymbol{x}$でしたがコサイン類似度を用いる場合は$z_k = \cos(\theta_{\boldsymbol{w}_k, \boldsymbol{x}})$となります。
他の類似のものとしてSphereFace、
L_{sphere}=\log(1 + \frac{\sum^K_{k \neq y}e^{sz_k}}{e^{s\cos(m_1\arccos z_y)}})
SosFace、
L_{sphere}=\log(1 + \frac{\sum^K_{k \neq y}e^{sz_k}}{e^{s[\cos (\arccos z_y) + m_2]}})
ArcFace、
L_{sphere}=\log(1 + \frac{\sum^K_{k \neq y}e^{sz_k}}{e^{s(z_y - m_3)}})
などが有名です。$m_1$,$m_2$,$m_3$はinter-class marginの制御パラメータです。
なお、これらのlossはすべて分母にのみ工夫があるのがわかるかと思います。
The Intra-Class Component
intra-class objectiveがinter-class objectiveにどのように絡み合っているかを確認します。
先程のlossはすべて分子部分は同じでした。それを$M$とします。つまり
M=\sum^K_{k\neq y}e^{sz_k}
とします。そうするとsoftmax lossは
L_s=\log(1 + \frac{\sum^K_{k \neq y}e^{sz_k}}{e^{sz_y}})=\log(1 + \frac{M}{e^{sz_y}})
となります。この$M$はinter-class similarityを表しています。$M$が大きいというのは正解クラス以外との類似度が大きいということを意味します。
$M$を固定して$z_y$とlossの関係をプロットしたのが下記の図2(a)になります。

このグラフから2つのことがわかります。
-
Mの値に関わらずどれも区分線形関数のような形をしています($z_y$が小さいときは$L_s \rightarrow \log{M}-sz_y$、$z_y$が大きいときは$L_s \rightarrow 0$)。つまり、intra-class similarity $z_y$が小さいときはほぼ一定の勾配が流れますが、$z_y$が大きくなれば勾配はほぼ0になります
-
勾配が変化する変曲点は$M$と相関があり、区分線形関数の交点$d$は
d=\frac{\log{M}}{s}
で表せます。$d$で勾配がほぼ消えるため、$d$は最適化の終点ともみなせます。
これらのことから
Conclusion #1
目的関数としてsoftmaxを用いると、inter-class similarity($M$)が小さくなれば、intra-class objectiveが小さい値でも学習が終了する。
つまり、intra-class objective の最適化は不十分なまま、早くに学習が終了してしまいます。
図2で他のsoftmax lossファミリーと比較してみると、同じ値の$M$でもただのsoftmax lossに比べArcFaceなどの学習終了点(lossが0になる箇所)は大きく右にシフトしていることが確認できます。
つまり、これらのlossは$z_y$が0.8以上の大きな値でもintra-class objectiveの最適化が止まらないということを示しています。
この問題は学習が進むに連れ$M$が小さくなってしまうことが原因です。そこで$M$を定数で置き換えます。定数を$\epsilon$として$M$を$\epsilon$で置き換えた
L^{intra}_D=\log(1 + \frac{\epsilon}{e^{sz_y}})
がintra-classコンポーネントのlossとなります。
The Inter-Class Component
intra-class objectiveを取り出せたので、次はinter-class objectiveです。
先程の$ L_D^{intra}$ だけではinter-class objectiveの項がありませんのでデータを適当な1点にマッピングする可能性があります。これを避けるためにはinter-class objectiveを満たす正則化的なものが必要です。
今度もsoftmax lossやそのファミリーの解析をしていきましょう。
データサンプルを$x$、その正解クラスを$y$、そして$n\neq y$クラスの出力を$z_n$とするとsotmax lossは
\log(1 + \frac{\sum^K_{k \neq y}e^{sz_k}}{e^{sz_y}})=\log(1 + \frac{e^{sz_n} + \sum^K_{k \neq y,n}e^{sz_k}}{e^{sz_y}})=\log(1 + \frac{e^{sz_n} + M_n}{e^{sz_y}})
と書けます($M_n=\sum^K_{k \neq y,n}e^{sz_k}$)。
初めに$M_n$を固定していくつかの$z_y$に対してのlossと$z_n$の関係をプロットして確認します(図3(a))。
勾配$\frac{\partial L_s}{\partial z_n}$は$z_n$が大きいときはほぼ一定である点で0になる、先程のintra-class objectiveのと似たような形をしています。また$z_y$が大きい場合、lossは$z_n$の値に関わらずほぼ0になるのが確認できます。
これから
Conclusion #2
softmaxを目的関数としたとき、intra-class similarity($z_y$)が大きくなれば、inter-class objectiveの最適化も止まる
といえそうです。これは他のクラスとの距離を大きくするとという目的が不十分な状態で終わり、metric learningなどの妨げになってしまいます。
intra-classコンポーネントと同様に区分線形関数との交点を学習の終了点として
d'=\frac{\log(e^sz_y+M_n)}{s}
と定義します。図3(b)にsoftmaxファミリーについて$d'$と$z_y$の関係をプロットしました。曲線のプラトーが広いほど、inter-class similarityの正則化が強いことを示しています。ただのsoftmax以外は広いプラトーがあるのがわかりますね。
広いプラトーを得るにはどうすればいいか、intra-class objectiveのときのように今度は$e^{sz_y}$を定数にすることで解決できます。ここでは単純に$e^{sz_y}=1$とし、
L^{inter}_D=\log(1 + \sum_{k \neq y}e^{sz_k})
がinter-classのコンポーネントになります。
D-Softmax and Its Light Variants
上記からからsoftmaxをDissectedしたloss(D-Softmax loss)は
L_D=L^{intra}_D + L^{inter}_D =\log(1 + \frac{\epsilon}{e^sz_y}) + \log(1 + \sum_{k \neq y}e^{sz_k})
となります。
D-Softmaxの利点は2つあります
1つ目は、embed vector等として使う際により良く別れた特徴となることです。普通のsoftmax lossではinter-class objectiveかintra-class objectiveのどちらかが達成されればもう一つの正則化が弱まってしまっていましたが、D-Softmaxでは常に正則化が効いているため学習が進んでもinter-class objectiveもintra-class objectiveも両方の最適化が行われます。
2つ目は絡み合っていた目的が別れたため膨大なクラスの場合などの計算コストを軽くできます。
2つ目について説明していきます。
クラス数が$10^6$を超え始めるとsoftmaxの計算が学習の時間的ボトルネックとなり始めます。
バッチサイズを$B$、クラス数を$K$としたとき、softmaxの計算オーダーは$O(BK)$です。D-softmaxの各コンポーネントでは、$L_D^{intra}$が$O(B)$、$L_D^{inter}$が$O(B(K-1))$となります。$K>>B$となるときには$L_D^{inter}$の計算コストが問題になってきますが、果たして、本当に正解以外のすべてのクラスについての計算をする必要があるのでしょうか。先に答えを述べるとNoです
学習後に得られるクラスベクトルはお互いに直行していてほしいのですが、そもそも、高次元において各クラスの代表ベクトル同士はどれだけ直行しているのでしょうか?
256次元の10,000クラスベクトルをランダムに初期化し、ペアを取り出したときのコサイン類似度の分布をプロットしたのが図4(a)なのですが0平均のガウシアンになっているのがわかります。図4(b)は学習後の分布ですが、少々分散が大きくなっているものの平均が0からほとんど変わらないガウシアンであることがわかるかと思います。
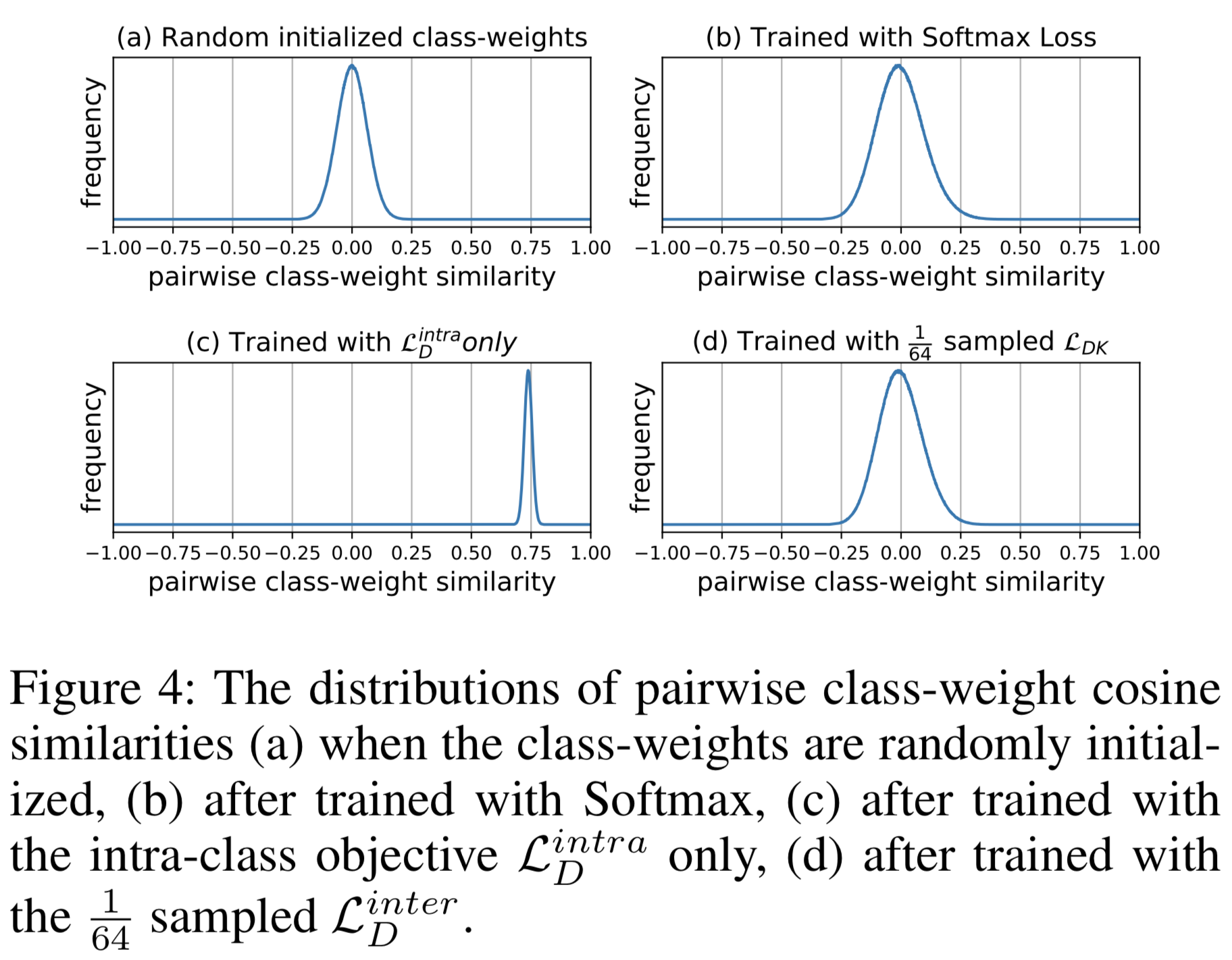
ここからもう一つの結論が得られます。
Conclusion #3
高次元の埋め込み空間を学習する場合、inter-class objectiveはクラスベクトルを離そうとするのではなく、(主に)初めの直行状態を維持しようとする正則化である。
そうすると、正解クラス以外のすべてのクラスについて計算する必要はなさそうです。
試しに$L_D^{inter}$において、「正解クラス以外のすべてのクラス」についてではなく「正解クラス以外の$K-1$クラスの中からサンプルした$\frac{(K-1)}{64}$クラス」で計算し、学習をしてみました。その結果が図4(d)です。予想通り「正解クラス以外のすべてのクラス」で学習した結果と比べても分布に大差ないことが確認できます。このあとの実験で精度を確認しますが、僅かな精度低下で64倍の高速化できることが確認できます。これをD-Softmax-Kと名付けます。式で書くと
L_{DK}=\sum^B_{i=1}\log(1+\frac{\epsilon}{e^{sz_{y_i}}}) + \sum^B_{i=1}\log(1 + \sum_{k \in S_K}e^{sz_k})
です。ここで$S_K=\{k|k=1,2,...,K\} \backslash \{ y_i|i=1,2,...,B \}$です。サンプリング数は速度と精度のトレードオフで、任意に選択できます。
また他のサンプリングの方法として、使用するクラスをサンプリングするのではなく、使用するデータサンプルをミニバッチからサンプルする下記をD-Softmax-Bと名付けます。
L_{DB}=\sum^B_{i=1}\log(1+\frac{\epsilon}{e^{sz_{y_i}}}) + \sum_{i \in S_B}\log(1 + \sum^{K}_{k =1}e^{sz_k})
$S_B$はミニバッチのサブセットです。$L_D^{inter}$の計算オーダー$O(B(K-1))$においてKを減らすのがD-Softmax-Kで、Bを減らすのがD-Softmax-Bということです。
Experiments
実験やデータセットの詳細ついては割愛させていただきます。興味のある方は論文を御覧ください。
性能評価に使用したデータセットはLFW、CFP-FP、AgeDB-30、IJB-C、そしてMegaFaceの計5つの顔認識データセットです。
事前学習としてMS-Celeb-1MとMegaFace2を使用しました。なおMS-Celeb-1Mにはアノテーションミスがあるそうで独自にクリーンしたそうです。MS-Celeb-1Mは85K人の5.8M枚、MegaFace2は672K人の4.7M枚となります。
Experiments on D-Softmax
まずはD-Softmaxについて。まずはterminate pointである$d$はどのくらいがいいのでしょうか。色々なdを調べたのが表1の真ん中あたりの行です。$0.5$から$0.9$に上がるに連れパフォーマンスがよくなっているのが確認できますが、$d=1.0$ではわずかに悪化しました。いくつかのデータセット、バックボーンでも調べましたが、どの設定でも$d=0.9$がよさそうなのが確認できます。なので、以降の実験では$d=0.9$とします。

同じデータセットとアーキテクチャを使ってNormFace($L_s$)、SphereFace($L_{sphere}$)、ArcFace($L_{arc}$)を学習し比較もしましたがD-softmaxの方が大体良い結果であることが確認できます($d=0.9$)。
ここでArcFaceを例にハイパーパラメータ$m$と$d$の違いを考えてみます。
$m$はサンプル特徴量とネガティブクラスの重みとの間に必要な角度マージンでintra-class objectiveとinter-class objectiveの両方に影響を与えます。そのためintra-classに関する制約はすべてのクラスについて同じ厳密さにはなりません。最適な$m$は他のハイパーパラメータによって変化する可能性があり、チューニングが必要です。それに対しD-Softmaxの$d$はより明確なintra-class制約で、どのクラスにおいても同じ厳密さになります。そのためD-Softmaxにおける最良のdの選択は、D-Softmax-Kなどのようにダウンサンプリングした場合でも一貫して0.8から0.9の範囲にあります。
Experiments on Light D-Softmax
高速化のためにサンプリング方法の異なるD-Softmax-BとD-Softmax-Kを提案しましたが、これらについての調査をします。
D-Softmax-B
D-Softmax-Bはミニバッチからinter-class objectiveの計算に使用するデータをサンプルするだけなので実装が楽です。
バッチサイズ$256$としたResNet-50にD-Softmax-Bを適用して、サンプリングレートを$1$から$1/256$について調査した結果が表2になります。サンプリングレートが$1/64$あたりから精度が低下していきます。$1/16$ぐらいなら精度低下も気にならず、かつ16倍の高速化ができます。また、サンプリングレートが$1/256$でもaccuracy 99.50%を保っていることからConclusion#3は正しそうで、全てのクラス$K$個についての計算は必要なさそうです。

ただ、GPUのメモリ制限も問題になります。 D-Softmax-Bの計算では、クラス重み行列全体をGPUメモリにコピーする必要があるため、並列処理が困難になります。
D-Softmax-K
D-Softmax-Kではミニバッチ内のデータ毎に使用するネガティブクラスをサンプリングして$L_KD^{inter}$を並列に計算できます。
また、大容量メモリ(CPU Ramなど)にすべてのクラスの重みを格納したパラメータサーバを用意し、サンプリングされ、必要なったクラスの重みをパラメータサーバ上からで取得しGPUにキャッシュすることでGPUのメモリ制限のジレンマが緩和されます。実装もそれほど複雑にはなりません。
しかし、同じサンプリングレートでD-Softmax-Bに比べ精度がわずかに劣ります(表2の灰色の行)。
これはD-Softmax-Kでは各イテレーションでクラスの重みの内一部が更新されますが、D-Softmax-Bでは、すべてのクラスの重みがミニバッチ毎に更新され、常に最新のものになっているためと考えられます。しかし、D-Softmax-Kの方が並列処理が容易であり性能の差はわずかであることを考慮すると大規模な訓練ではD-Softmax-Kを使用する方がよさそうです。
所感
inter-class objectiveとintra-class objectiveにlossを分けたことで、目的に合わせてlossを調整できるというのもなにか使えそうかもしれません(結果を可視化してみて$d$を調整...とかもやってみたいですね)。
softmaxを解析した結果は非常に興味深かったです。この論文のように解析して提案していく系の論文は知見も得られて面白いですね。個人的にはAdaCosがベースライン化してきたので、比較がなかったは少々残念でした。時期の問題でしょうか。
D-Softmax-Kなどの高速化については解きたい問題や目的によるとは思いますが、予備実験等に利用するのは良さそうですね。
